疲劳损伤演化方程必须能够描述绝大多数微裂纹成核与扩展行为的如下两个特征，即微裂纹的成核长度不超过晶粒的尺寸，以及微裂纹尖端扩展到第一个晶界处即停止扩展。由于此时的微裂纹已停止扩展，即：按照绝大多数微裂纹的成核与扩展行为和疲劳损伤变量的定义，得到多尺度疲劳损伤模型如下：同时得到多尺度疲劳损伤演化率为：......
2023-08-26
高低周疲劳交互作用下的疲劳损伤演化方程模拟分析
【摘要】：3.疲劳损伤多尺度模型利用方程（8－2）建立的宏观连续疲劳损伤与当前短、长裂纹密度的
要考虑疲劳损伤演化进程中短裂纹与长裂纹的共同作用，首先需要定义长、短裂纹共存时的疲劳损伤变量。
当金属材料的晶粒内部存在长度为ai的短裂纹时，对应的微损伤Di：
其中d为晶粒尺寸。
在晶粒内部的裂纹增长归结于短裂纹的成核与扩展。在3.2节的金属疲劳损伤多尺度表征方法中，由于忽略长裂纹对疲劳损伤累积的贡献，在微裂纹成核与扩展的描述中，是忽略了短裂纹突破晶界的可能性，假设所有短裂纹在晶界的阻碍作用下停止增长。事实上，当疲劳短裂纹扩展到晶界时，大多数短裂纹在晶界的阻碍作用下停止了增长，但是也会有少许突破晶界阻碍继续增长［37］。每一个突破晶界阻碍继续增长的短裂纹，都有可能与其他突破晶界或者达到晶界边缘的短裂纹汇合，如此也就有可能发展成为长裂纹。因此，为了考虑疲劳损伤演化进程中短裂纹与长裂纹的共同作用，应该放松对短裂纹在晶界的阻碍作用下停止增长的限制，来定义长、短裂纹共存时的疲劳损伤变量。
假定当前最大裂纹长度为amax，那么裂纹群体扩展所对应的疲劳损伤变量可以通过定义代表性体元中所有微损伤的平均值来定义：
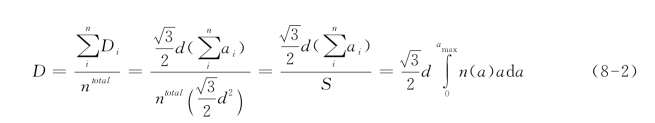
其中ntotal为代表体元中所包含的所有晶粒的数目，S为代表体元的总面积；n（a）为代表体元中尺寸为a的裂纹密度，即单位面积上裂纹数目。而这里的裂纹尺寸a是不限于短裂纹的尺寸，也就是说该尺寸可能大于晶粒长度，裂纹包括了短裂纹与长裂纹。为了利用所发展的疲劳模型进行疲劳损伤评估与寿命预测，需要通过研究长、短裂纹扩展过程中的疲劳损伤演化行为来得到裂纹密度n（a）的具体形式。
1.长、短裂纹的疲劳演化行为
在疲劳循环增量作用下的［N／Nf，N／Nf＋Δ（N／Nf）］之间疲劳裂纹萌生与扩展导致的疲劳损伤演化模式如图8.1所示。考虑到大多数短裂纹在晶界的阻碍作用下会停止增长，但是也有少许突破晶界阻碍继续增长，也就是说，短裂纹扩展到晶界时，会以概率P停止在晶界处，以概率1－P突破阻碍继续增长。图8.1中就考虑了疲劳裂纹演化的这两种情况。因此，在长、短裂纹共存的情况下，为了得到裂纹密度n（a，N／Nf）的表述，不仅需要定义短裂纹的成核与扩展率，而且还需要定义长裂纹的扩展率与短裂纹停止在晶界处的概率P。
短裂纹成核与扩展行为具有高度随机的特点，目前很少有模型能很好地完全描述短裂纹成核与扩展复杂的机理。参考仅有短裂纹（又称为微裂纹）存在时（3.2节中）所用的短裂纹成核率模型，这里选用更为简单的短裂纹的成核率
模型：
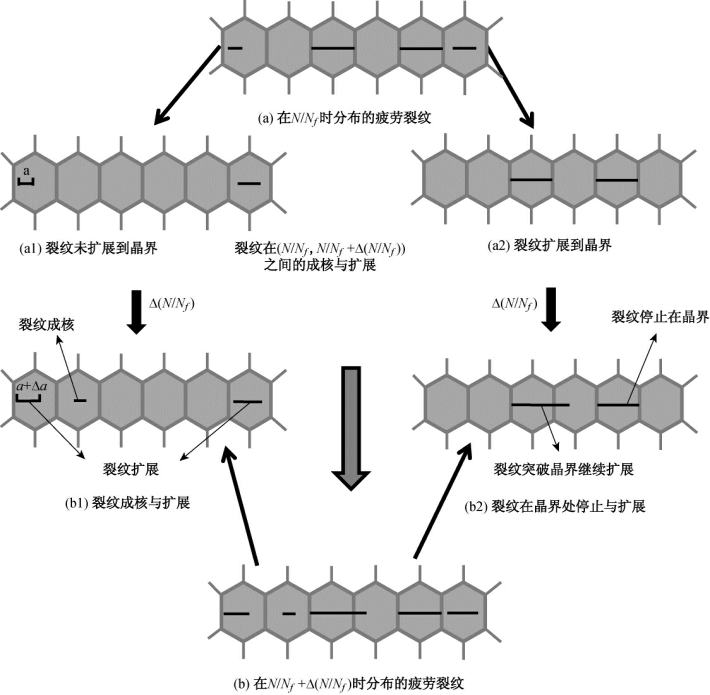
图8.1 疲劳裂纹演化模式示意图
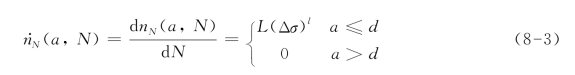
其中a为裂纹长度，L，l为模型参数。
在已有的关于金属疲劳问题的研究中，已经有一些描述疲劳短、长裂纹扩展率的模型，这里选用Miller等发展的描述疲劳短、长裂纹扩展行为的模型［13］：
其中A，α，B，β，C为模型参数，Δγ为剪应变幅值（对于单轴拉压状态下的疲劳损伤来说，应以应力范围Δσ或应变范围Δε代替Δγ），d0为微观构造尺寸。当施加的疲劳荷载低于疲劳极限时，d0的值取为约0.1mm，接近晶粒的尺寸［13］。这里所采用的描述疲劳短、长裂纹扩展率
的模型可表示为：
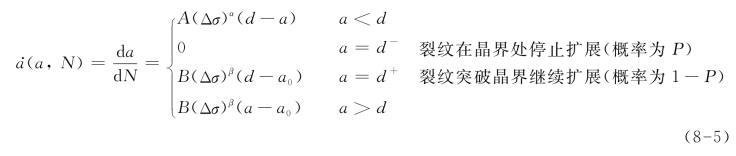
其中a0为模型参数，P为短裂纹在晶界处停止扩展的概率。因为裂纹在晶界处停止扩展具有高度的随机性，因此在已有的关于金属疲劳的研究中，很少有给出短裂纹在晶界处停止扩展的概率P的模型。通过对疲劳实验的微观观测，可以发现大多数的短裂纹会在晶界处停止扩展，随着应力幅值的增加，越来越多的短裂纹会突破晶界的阻碍继续增长。因此，短裂纹在晶界处停止扩展的概率被认为与疲劳应力幅值成反比，据此选定短裂纹在晶界处停止扩展的概率P的模型为：
其中E与q为模型参数。
2.描述长、短裂纹群体共同演变效应的疲劳损伤演化方程
描述短裂纹成核与扩展的模型、长裂纹扩展的模型与短裂纹在晶界处停止扩展的模型已由方程（8－3）、（8－5）与方程（8－6）给出。利用这些描述疲劳短、长裂纹成核与扩展行为的模型，可推导得到群体短、长裂纹共同演化的疲劳裂纹密度方程。下面分别考虑疲劳裂纹扩展的几种情况对裂纹密度函数进行量化分析。
（1）对于在晶粒内部扩展的短裂纹（a＜d）的情况，如图8.1（a1）与图8.1（b1）所示，尺寸在（a，a＋Δa）之间的短裂纹在疲劳循环比例［N／Nf，N／Nf＋Δ（N／Nf）］之间所增加密度表示为：
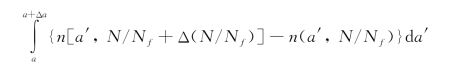
其中短裂纹密度增加的第一个原因是由在此阶段中短裂纹的成核所造成：
短裂纹密度增加的第二个原因是由在此阶段中短裂纹的扩展所造成：
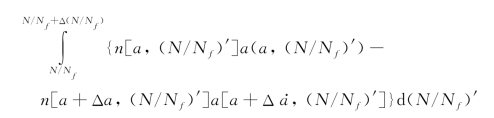
当Δ（N／Nf）→0，Δa→0，根据以上三部分得到在晶粒内部短裂纹密度演化方程：
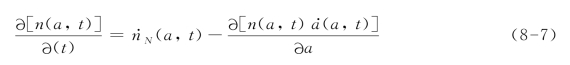
其中t＝N／Nf，根据方程（8－3）与方程（8－5），
可分别表示为：
利用方程（8－8）与方程（8－9），并结合初始的条件n（a，0）＝0，可以得到方程（8－3）的解，即在晶粒内部短裂纹（a＜d）的密度可以表示为：
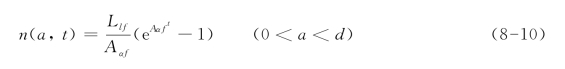
其中Llf＝L（Δσ）l Nf，Aαf＝A（Δσ）αNf。
（2）对于短裂纹达到晶界处（a＝d）的情况，如图8.1（a2）与图8.1（b2）所示的情况，短裂纹停止在晶界处的概率为P，突破晶界的阻碍继续扩展的概率为1－P，分别对应于方程（8－9）中a＝d－与a＝d＋两种情况，与得到晶粒内部短裂纹密度演化方程（方程（8－7））类似，可以得到短裂纹达到晶界（a＝d）处时，裂纹密度演化方程：
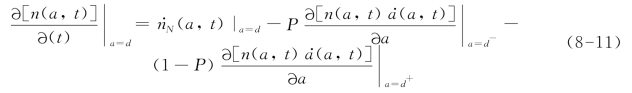
根据方程（8－6）、（8－8）与方程（8－9），并结合初始的条件n（a，0）＝0，方程（8－11）的解，即短裂纹达到晶界（a＝d）处时，裂纹密度可以表示为：
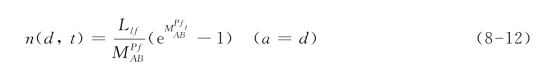
其中
。
（3）对于裂纹突破晶界阻碍继续增长（a＞d）的情况，当前的裂纹密度完全依赖于（1－P）n（d，t0），这种情况（a＞d）的裂纹密度可以表示为：
其中t0可根据方程（8－9）中a＞d时的裂纹扩展率和当前的t得到：
其中当前最大的裂纹长度amax可以根据不等式t0≥0，获得：
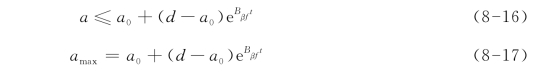
根据方程（8－15）与方程（8－17），方程（8－13）可以重新表示为：
至此，在N／Nf时，当前所有情况的疲劳短、长裂纹的密度函数已经全部得到，分别为：方程（8－10）、（8－12）与方程（8－18）。
3.疲劳损伤多尺度模型
利用方程（8－2）建立的宏观连续疲劳损伤与当前短、长裂纹密度的关系，以及所获得的当前所有情况的疲劳短、长裂纹的密度函数，即方程（8－10）、（8－12）与方程（8－18）。连接连续均匀的疲劳损伤与群体短、长裂纹共同演化行为关系的多尺度的疲劳损伤模型可以表示为：
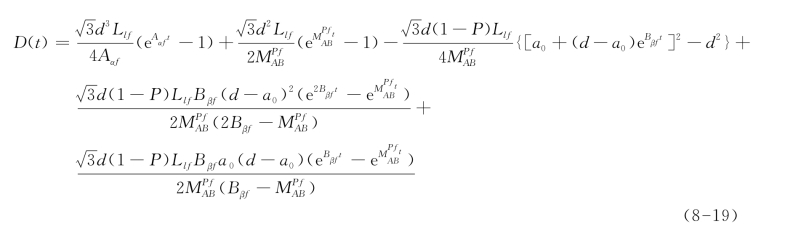
方程（8－19）的左边为连续均匀的疲劳损伤变量，是一个度量疲劳引起的宏观材料性能退化程度的宏观物理量，而在方程的右边是由描述群体短、长裂纹共同演化行为的变量构成的微细观尺度下的度量。如将方程（8－19）表示为关于疲劳循环变量N的方程：
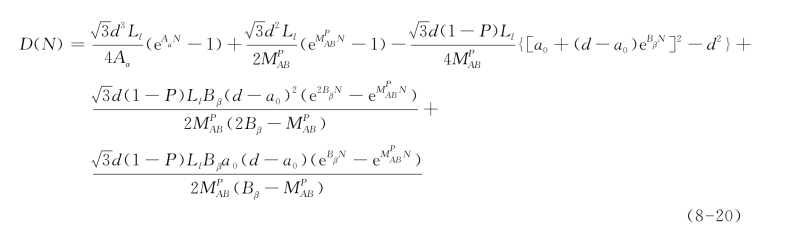
其中
。
结合方程（8－20）与条件D＝1时N＝Nf，可以通过求解如下的方程来估算疲劳寿命Nf。
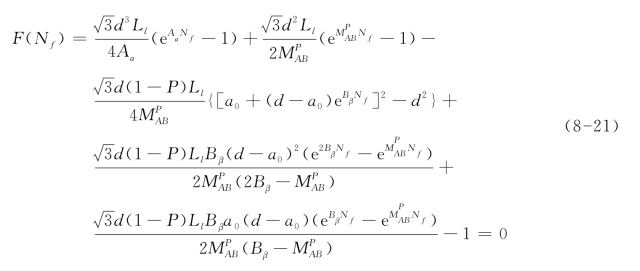
有关结构损伤多尺度模拟与分析的文章
- 详细阅读
-
疲劳损伤演化过程分析案例：短、长裂纹共同扩展详细阅读
图8.11短、长裂纹群体共同演化过程的多尺度模拟和分析结果综上所述，针对金属材料及结构在复杂服役环境下的高、低周疲劳交互作用的损伤问题，须在疲劳损伤演化过程中考虑短裂纹与长裂纹同时存在且共同演化的情况，建立结构中的宏观唯象疲劳损伤变量与材料内部群体短裂纹与长裂纹共同演化行为之间相互关联的关系的多尺度疲劳损伤模型。......
2023-08-26
-
结构损伤多尺度模拟与分析：桥梁钢箱梁疲劳损伤详细阅读
桥梁上的正常服役荷载一般在结构中产生高周疲劳损伤的累积，而强震台风等灾害荷载会导致结构中已累积损伤的高应力区域在短时间内发生低周疲劳损伤演化。因此，在桥梁钢箱梁结构的疲劳损伤演化过程分析中，首先要解决如何模拟高、低周疲劳交互作用下的疲劳损伤演化过程的问题，建立疲劳损伤演化过程中群体短裂纹和长裂纹共同演化行为的本构描述。......
2023-08-26
-
混凝土柱地震荷载下损伤演化模拟与分析详细阅读
第二个案例是在模拟地震荷载下混凝土柱的损伤演化致失效分析。图6.38混凝土柱试样［36］图6.39试验中施加的荷载谱应用前述的损伤演化致失效的跨尺度自适应模拟与分析方法对如图6.38所示的混凝土柱试样在试验模拟的地震荷载作用下的跨尺度损伤演化过程进行模拟，模拟结果见图6.40。通过将所模拟的混凝土柱在模拟地震荷载下的损伤演化过程的数值结果与实验结果进行对比，表明数值模拟结果与实验结果吻合较好，表明所发展的算法是可靠的。......
2023-08-26
-
混凝土材料细观损伤演化过程模拟的基本方程在结详细阅读
在基于材料细观构造图像建立了混凝土细观模型以后，还需要确定计算混凝土材料细观损伤演化过程的基本方程，包括由混凝土各细观组分材料性能决定的材料刚度矩阵计算、各细观组分材料的损伤演化率等。对于大尺寸的混凝土土木工程结构，则必须发展损伤跨尺度演化过程的自适应模拟与分析方法。......
2023-08-26
-
结构损伤分析：疲劳裂纹萌生机制分析详细阅读
由图可见，疲劳裂纹萌生于试样内部预制裂纹尖端存在初始缺陷的位置，再逐步扩展至试样表面，形成了试样内部疲劳裂纹尖端“领先”表面裂纹扩展的现象。图2.30试样疲劳断口及其分区图2.31疲劳裂纹源区的电镜观测图像......
2023-08-26
-
疲劳裂纹出现过程中的损伤多尺度分析详细阅读
根据前述疲劳裂纹的萌生与演化机制的分析，演化过程可分为斜腹杆内部疲劳微裂纹萌生、扩展至表面可见裂纹与表面裂纹扩展这样三个阶段。由此可见，尽管损伤从材料层次到构件层次的演化并非跨尺度过程，其材料层次特征响应演化规律的变化也预示着构件层次特征响应的演变，材料层次损伤演化即疲劳微裂纹加速扩展的阶段同样可视为构件损伤跨层次演化的特征。......
2023-08-26
-
结构损伤多尺度模拟与分析：混凝土损伤特征与演详细阅读
构件受力后，钢筋和混凝土之间有相对滑移趋势时，产生摩阻力。这个过程就是钢筋混凝土粘结界面的损伤演化过程。现行钢混结构设计理论大多是基于平截面假定进行的，这隐含着钢筋和混凝土这两种性质截然不同的材料粘结良好，以确保二者变形协调。保障钢筋和混凝土的粘结良好是确保钢混结构安全的重要条件之一。图2.44钢筋与混凝土粘结失效引发的结构破坏......
2023-08-26
相关推荐