在PBX 细观损伤的实验研究方面，国内外众多学者已有过不少的研究。Palmer 等［19］和Chen 等［20］在对PBX 间接拉伸的实时显微实验中观察到了颗粒断裂、界面脱黏、黏结剂基体开裂等多种损伤破坏形式。Chen 等［21］和Palmer 等［19］对PBX 的破坏性质进行了研究。Rae 等［23］首次将高灵敏度的云纹干涉法应用到PBX 材料的细观变形破坏研究，主要将巴西实验与云纹干涉法相结合。......
2023-06-27
钢筋混凝土拉拔构件细观损伤分析模型
【摘要】：图6.17钢筋混凝土拉拔试样损伤分析的细观模型钢筋混凝土粘结性能的劣化主要是粘结界面区的缺陷及混凝土的细观结构弱化导致的，在界面区的细观模拟中，钢筋采用线性弹性本构关系，砂浆与粗骨料采用含损伤后的混凝土本构关系。如图6.18所示的弹性损伤本构关系模型可表示为：式中，Em与Ea分别为砂浆与粗骨料的初始弹性模量。
钢筋混凝土拉拔试验是研究钢筋混凝土粘结性能及其拉拔性能劣化的主要方法，因此，为了解钢筋混凝土粘结界面损伤性能和具体介绍粘结界面损伤模拟方法，这里首先针对钢筋混凝土性能试验中常用的拉拔试件来建立粘结界面细观损伤分析模型。
常用的拉拔试验装置如图6.15所示，钢筋上端布置位移计可测得钢筋自由端滑移，钢筋下端连接试验机为试件加载。拉拔试件尺寸如图6.16所示，构件的上下部钢筋与混凝土之间均有一个长50mm的PVC缓冲套筒，故在总高180mm的拉拔试件中的钢筋与混凝土的有效粘结长度为80mm。
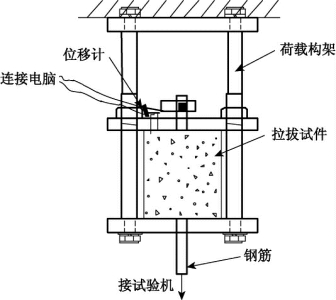
图6.15 拉拔试验装置示意图
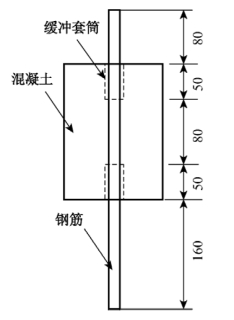
图6.16 拉拔试件尺寸
钢筋混凝土拉拔构件沿钢筋中轴线对称，同时约束和荷载也成对称分布，所以在对拉拔试件进行建模时沿钢筋中轴线取其中的一半进行建模。根据拉拔试验过程中试样上所承受的荷载与边界约束对模型进行约束与加载，考虑到对称性，钢筋中轴线处水平方向的位移始终为0，故对模型的钢筋中轴线处的水平方向施加固定约束。由此建立的钢筋混凝土粘结界面细观损伤模型如图6.17所示。图中混凝土中的粗骨料组分为图中蓝色的单元，其中的材料本构关系为σa＝f（εa，Da）；砂浆组分为图中浅灰色的单元，其中的材料本构关系为σm＝f（εm，Dm）；其中，Da，Dm分别为骨料和砂浆组分中的损伤变量。钢筋组分为图中红色的单元，其中的材料本构关系为σs＝f（εs）。
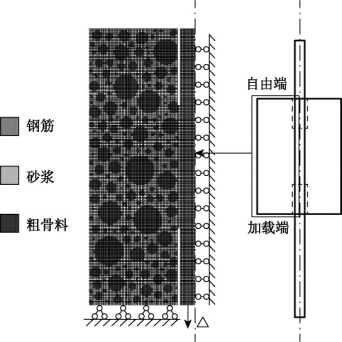
图6.17 钢筋混凝土拉拔试样损伤分析的细观模型（彩图见附录）
钢筋混凝土粘结性能的劣化主要是粘结界面区的缺陷及混凝土的细观结构弱化导致的，在界面区的细观模拟中，钢筋采用线性弹性本构关系，砂浆与粗骨料采用含损伤后的混凝土本构关系。
钢筋本构关系方程如下：
式中，Es为钢筋的弹性模量。
砂浆材料与粗骨料材料的本构关系均采用如图6.18所示的损伤本构模型［28］，但模型中的各个性能参数将根据砂浆与粗骨料各自的材料性能分别取值，不同组分的性能参数就构成了砂浆与骨料的不同的本构关系，以模拟混凝土中存在的不同组分的材料性能及其非均匀特性。
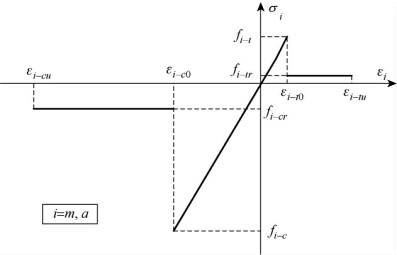
图6.18 粗骨料与砂浆材料单轴弹性损伤本构模型
从图6.18可以看出这里的粗骨料与砂浆材料的力学模型比较简单，而混凝土材料非线性分析中常用的本构关系比这个要复杂得多。这是由于如若将混凝土材料视为宏观上均质连续材料，其损伤以后的本构关系必然是非线性本构关系；而这里的混凝土细观模拟是考虑了混凝土细观组分的非均匀性，虽然对材料中的每个组分采用了简单的本构关系，混凝土的非线性损伤行为仍然可以通过各个细观组分之间的协调变形性能及其损伤演化过程来描述。这里采用的是细观力学的基本理念：用细观尺度上各组分的简单本构关系来描述宏观尺度上所有组分的复合体的复杂本构行为。
如图6.18所示的弹性损伤本构关系模型可表示为：
式中，Em与Ea分别为砂浆与粗骨料的初始弹性模量。参考文献中的单轴压缩试验［29］获得的混凝土破坏强度与常用强度混凝土的数值“配比方案”［30］，取Em的参考值为22.2GPa，Ea的参考值为75GPa，混凝土弹性模量Ec的参考值为31.5GPa。
在单轴拉伸时损伤变量Dm与Da的表达式如下：
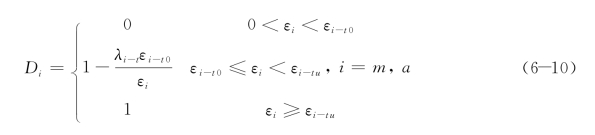
式中，εi－t0为损伤拉应变阈值，εi－tu为极限拉应变；用关系式fi－tr＝fi－tλi－t定义拉伸残余强度系数λi－t，fi－t为单轴抗拉强度，fi－tr拉伸损伤后的单元残余强度。
在单轴压缩时的损伤变量Dm与Da的表达式如下：
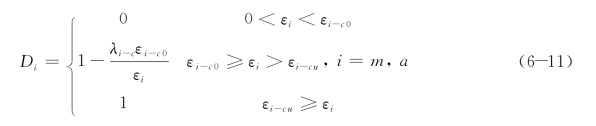
式中，εi－c0为损伤压应变阈值，εi－cu为极限压应变；用关系式fi－cr＝fi－cλi－c定义压缩残余强度系数λi－c，fi－c为单轴抗压强度，fi－cr压缩损伤后的单元残余强度。
有关结构损伤多尺度模拟与分析的文章
- 详细阅读
-
钢筋混凝土拉拔损伤演化的多尺度模拟详细阅读
第一个案例是钢筋混凝土拉拔构件损伤演化致拉拔失效过程分析。在拉拔力－位移曲线的线性段，构件中靠近钢筋处只有部分局部发生损伤，其后钢筋附近的细观损伤区域越来越多，当拉拔力达到峰值（F点）以后，钢筋两侧已经都发生损伤，随着拉拔位移增加、损伤值不断增加达到脱粘阈值，导致拉拔力不断下降直至拉拔失效。......
2023-08-26
-
高聚物黏结炸药的细观尺度损伤破坏模拟详细阅读
PBX 中颗粒与黏结剂之间的脱黏预测是非常重要的，因为更复杂的应力分布与脱黏破坏有关。他们认为，随着HMX 颗粒体积分数的增加，PBX 断裂阈值降低。Wang等［70］进一步发展了HMX 晶体及其黏合剂和界面的损伤模型，研究了PBX 9501 的动态力学行为和细观损伤演化机理。图1－5PBX 细观破坏模式1—界面脱黏；2—穿晶断裂；3—颗粒挤压升温......
2023-06-27
-
宏细观损伤与结构响应的分析分析详细阅读
图2.38各焊接试样损伤演化过程宏细观关联性对比图2.39试样中的微孔洞和微裂纹演化过程以上分析表明，焊接构件内部缺陷的体积、类型、分布及其演化过程都在一定程度上影响了构件的延性损伤演化过程，微裂纹的演化是导致焊接构件卸载弹模迅速折减的主要因素，均匀分布的微孔洞和微裂纹之间的相互作用较易导致构件萌生宏观主裂纹并迅速发生断裂。......
2023-08-26
- 详细阅读
-
结构损伤多尺度模拟：细观损伤演化对连接抗震性详细阅读
从图4.22和图4.23可以看出，损伤演化的速度随着构件截面的减小而加速。图4.22加载过程中梁腹板上的损伤演化过程图4.23加载过程中梁翼缘上的损伤演化过程3.易损区域损伤演化对框架节点地震响应的影响基于上述关于易损局部损伤分布的分析，进一步研究分布损伤的演化过程对构件地震行为和承载能力的影响，其中对动态应力和抗震性能的影响是通过考虑局部损伤演化计算的结果与忽略损伤演化的计算结果之间的比较来考察。......
2023-08-26
-
混凝土材料细观损伤演化过程模拟的基本方程在结详细阅读
在基于材料细观构造图像建立了混凝土细观模型以后，还需要确定计算混凝土材料细观损伤演化过程的基本方程，包括由混凝土各细观组分材料性能决定的材料刚度矩阵计算、各细观组分材料的损伤演化率等。对于大尺寸的混凝土土木工程结构，则必须发展损伤跨尺度演化过程的自适应模拟与分析方法。......
2023-08-26
-
混凝土细观模型建立方法，基于材料细观构造图像详细阅读
为了真实描述混凝土内部的细观构造，细观尺度下的混凝土模型须基于材料细观构造图像来构造和建立。这里基于图像重构混凝土细观有限元模型的方法可以概述为：首先将混凝土的细观图像转为由具有不同灰度值的像素点构成的灰度图像，如图6.27所示。图6.27基于图像的混凝土细观模型建立方法示意图众所周知，混凝土中骨料与基体之间的界面层是易于损伤演化的薄弱层，对混凝土损伤演化及宏观力学性能的影响很大。......
2023-08-26
相关推荐