图7-8 风向γ=3°时风电场等效模型3.风电场故障电流特征仿真t=4s时刻，在主变压器低压侧F1点发生三相金属性短路，故障持续时间为0.1s，故障后5ms风电机组投入Crowbar电路，故障前STH风电场输入风速为10m/s。动作电流与制动电流均不再恒定并叠加有其他频率分量，会发生大范围抖动。......
2025-09-29
四点弯曲梁损伤算例分析结果
【摘要】：图6.4损伤跨尺度演化过程模拟得到梁的位移－荷载曲线由图6.4可见，梁的损伤跨尺度演化导致梁的破坏是一个典型的脆性断裂破坏。从位移－荷载曲线可以明显地区分出梁中的损伤演化经历在梁的变形上反映出来的线性阶段、强化阶段、跳回阶段以及尾部阶段。这说明了梁中部高应力区域的损伤跨尺度演化过程对梁在宏观尺度下响应的显著影响。图6.6损伤演化过程中梁中性轴的移动
取梁长度L＝1 200mm（1.2 m），高度H＝200mm，混凝土弹性模量取为30GPa，骨料体积比为45%，砂浆断裂能为Gmotar＝40J／m2，可计算得到梁的荷载－位移P－Δ曲线如图6.4所示。
按照材料力学理论可得该四点弯曲梁的强度与材料强度的关系如下：
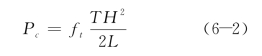
若取材料拉伸强度ft＝3 MPa，T＝1mm，可计算得到Pc＝50N／mm。这与图6.4所得出的最大荷载60N／mm基本吻合。值得注意的是，这里的计算过程中没有引入任何材料应力强度参数，仅仅是利用所建立的损伤多尺度模型对以微细观尺度下的裂纹扩展为主导的损伤跨尺度演化过程进行模拟，获得了宏观尺度下梁的极限荷载。
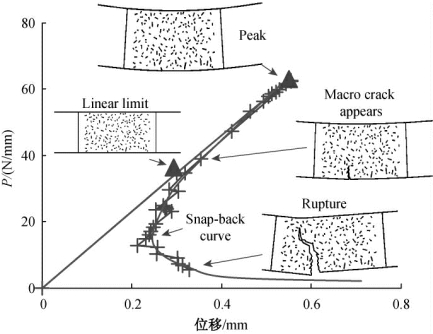
图6.4 损伤跨尺度演化过程模拟得到梁的位移－荷载曲线
由图6.4可见，梁的损伤跨尺度演化导致梁的破坏是一个典型的脆性断裂破坏。从位移－荷载曲线可以明显地区分出梁中的损伤演化经历在梁的变形上反映出来的线性阶段、强化阶段、跳回（snap－back）阶段以及尾部阶段。其中跳回（snap－back）的本质是：此阶段若想维持材料内部结构的稳定状态，施加的外力和变形必须同时减小才能实现。这是由材料内部损伤不可控演化或能量不可控释放所导致的，也是脆性破坏的一种常见现象。但是在一般的非线性力学响应计算中，使用迭代算法很难（或无法）获得这样的模拟结果。由于此阶段的力学行为不仅是非线性而且是非稳定，因此在物理实验中也很难捕捉到。(https://www.chuimin.cn)
图6.4还同时给出了梁在各个宏观的荷载－位移状态下混凝土内部多尺度损伤演化的临界状态。可以看出，在弹性变形的极限状态下，材料内部所有微裂纹都处于未扩展状态。超过弹性状态后，微裂纹开始分布式扩展，同时出现一些小规模的微裂纹聚合，但在宏观尺度下尚无法观测到。直到荷载－位移曲线的峰值点以前，梁中都未出现宏观裂纹。这也反映了强脆性断裂的一个特征，即在构件或结构中出现可见的宏观裂纹之前，就已几乎失去承受荷载的能力。在本案例中，宏观裂纹在图6.4中曲线上的跳回阶段才开始出现并持续扩展。到达位移－荷载曲线的尾部时，梁又部分恢复变形能力，位移开始出现增长，这个现象是由宏观裂纹与微观结构之间的摩擦、抑制所产生，下面给出的损伤演化过程中的应力云图可较为清晰地印证这一点。
图6.5给出损伤跨尺度演化过程中的几个典型时刻的应力云图（弯曲正应力σz），同时可观察到对应的裂纹形态。图6.5（b）给出了底部开始出现宏观裂纹时的情况。需要说明的是，宏观裂纹自动出现在拉应力最大的区域。在宏观应力场的诱导下，破裂位置的随机性中存在必然性。不管颗粒如何随机分布，几乎可以确定的是梁中的宏观裂纹会从底部萌生，而出现在底部位置的哪里则是随机的。图6.5（c）、（d）、（e）则显示了宏观裂纹扩展被骨料所阻止的情形。宏观裂纹改变了扩展方向，然后继续往前扩展，该过程即对应于图6.4中的尾部阶段。
图6.5 梁跨中区域损伤演化过程中的应力云图（彩图见附录）
图6.6显示了损伤跨尺度演化过程中梁的中性轴在裂纹前端区域不断上移的过程。这说明了梁中部高应力区域的损伤跨尺度演化过程对梁在宏观尺度下响应的显著影响。
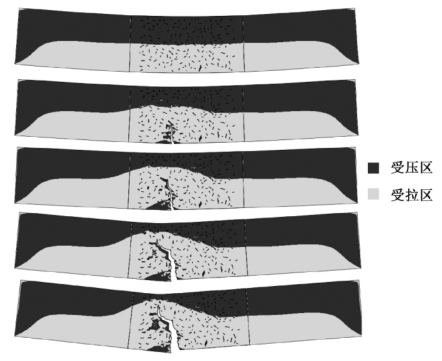
图6.6 损伤演化过程中梁中性轴的移动
相关文章
- 详细阅读
-
结构损伤指标分析结果详细阅读
目前工程结构中已经有一些常用的结构损伤状态评判指标，为比较我们提出的结构损伤表征与这些损伤指标之间的关联，这里将工程结构中常用的结构损伤状态指标归纳如下。这种基于结构动态响应定义的结构损伤指标主要应用于结构损伤识别领域对于结构损伤是否发生进行判断。基于模态应变能的损伤指标是应用较多的。此外，该模型不能获取结构地震响应中局部损伤的细节。FDR在正、负荷载循环中取较大值。......
2025-09-30
-
交直流混合输电系统算例分析详细阅读
交流母线额定电压都为220 kV，直流系统为双桥结构、双极运行，即每个换流站有四个换流变压器。图3.2系统接线图逆变侧换流变压器的参数如下：换流变压器单极容量300 MV·A；变压器漏抗12%；变压器交流侧电压230 kV；直流侧电压96 kV，可计算得出Xci。图3.3潮流计算的收敛特性由图3.3可知，交替迭代计算5次后，交直流系统潮流计算收敛。......
2025-09-29
-
半圆盘弯曲实验模拟结果分析详细阅读
对不同预制裂纹长度的半圆盘实验进行有限元建模分析。图4－7 所示为预制裂纹长度为0.96 mm 时，实验及数值模拟得到的载荷－位移曲线。从图中可知，计算结果和实验结果吻合较好，说明黏聚裂纹模型适用于半圆盘弯曲实验的力学性能分析。......
2025-09-29
-
梁的弯曲强度条件优化详细阅读
图7-26简支矩形木梁分析：画出梁的弯矩图。根据弯矩图可以看出根据弯曲正应力的强度条件。由图7-27可知，梁中点截面为危险截面，其最大弯矩为由梁的弯曲强度条件经查附录，可选用28b，其Wx=534 cm3。验算梁的强度按有关设计规范，最大工作应力若不超过其许用应力的5%是允许的。已知灰铸铁的Iz=7.56 ×106 mm4，抗拉许用应力[σ] +=39.3 MPa，抗压许用应力[σ] -=58.8 MPa，试校核该梁的强度。根据式故T 形梁强度不足。......
2025-09-29
-
经典算例展示与分享详细阅读
图9.9弹靶侵彻过程提取弹丸的速度-时间曲线，如图9.10所示。采用cm-g-μs单位制。有限元模型如图9.12所示。表9.1常见炸药的JWL参数所需拼接盖板长度L=l+13mm=mm=580.12mm，取580mm。......
2025-09-29
- 详细阅读
-
正应力分布规律及图示：梁弯曲的线性变化详细阅读
通过进一步的分析可知，各层纵向纤维的线应变沿截面高度应为线性变化规律，从而由虎克定律可推出，梁弯曲时横截面上的正应力沿截面高度呈线性分布规律变化，如图7-2所示。图7-1梁的弯曲应力图7-2梁弯曲时，正应力分布规律......
2025-09-29
相关推荐