如图4.10所示，在跨尺度界面上小尺度下的精细单元模型上的某一节点与大尺度下的梁单元节点之间的位置关系，并在跨尺度连接界面处建立局部坐标系xyz。为保证跨尺度界面上位移的协调性，需要在不同尺度单元在跨尺度界面上提出恰当的协调条件。......
2025-09-30
嵌套多尺度方法的算法与程序验证
【摘要】：根据前面所介绍的串行嵌套多尺度实施方法，对一些简单算例进行分析，以验证算法的可行性及有效性，并测试两种不同方法的计算能力、计算精度及效率。表5.2不同方法计算所得等效刚度参数单位：GPa2.单轴拉伸宏观等效力学性能验证为验证嵌套多尺度方法用于材料损伤后的力学性能分析的可行性，对如图5.3所示的体元在单轴拉伸作用下损伤后的等效力学性能进行计算。图5.4考虑局部损伤演化的宏观等效应力与忽略损伤的比较
根据前面所介绍的串行嵌套多尺度实施方法，对一些简单算例进行分析，以验证算法的可行性及有效性，并测试两种不同方法的计算能力、计算精度及效率。
首先对如图5.3所示的一个含多个夹杂的体元进行嵌套多尺度有限元分析，以验证所编写程序的有效性和可行性。所分析的体元为一长宽高分别为10mm的立方体，建模时采用的单元类型为八节点六面体减缩积分单元（C3D8R）。该体元的细观代表性体元RVE中间含有一个圆柱形夹杂，其RVE材料参数采用表5.1所示。由于夹杂的性能远远高于基体，因此分析中只考虑基体损伤的情况。
表5.1 细观RVE中各组分材料属性
图5.3 宏细观体元示意图
1.等效刚度的验证
通过在不同方向施加等效于单位初始应变的均布面力来获得细观应力影响函数
，对RVE内每个积分点上的细观应力影响函数
进行平均化即可求得如下式的宏观尺度上的等效刚度矩阵
。
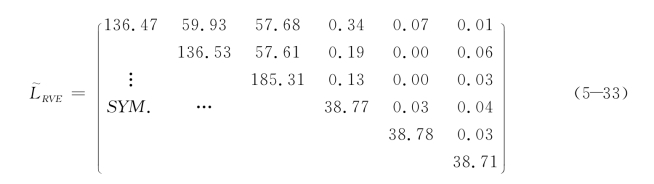
为了验证嵌套多尺度方法计算等效宏观刚度的有效性，将所计算的宏观等效弹性性能与细观力学中的自洽理论（Self－Consistent Method）和Mori－Tanaka方法（MTM）的计算结果进行比较，结果如表5.2所示。从表中可以看出，均匀化方法计算的宏观等效刚度与自洽理论、Mori－Tanaka方法计算的结果是相吻合的，从而验证了均匀化方法计算等效宏观力学性能的有效性。(https://www.chuimin.cn)
表5.2 不同方法计算所得等效刚度参数 单位：GPa
2.单轴拉伸宏观等效力学性能验证
为验证嵌套多尺度方法用于材料损伤后的力学性能分析的可行性，对如图5.3所示的体元在单轴拉伸作用下损伤后的等效力学性能进行计算。计算中所采用损伤判据为延性损伤判据，损伤变量D为等效塑性应变ε－p的函数：
其中
为单元完全损伤时（D＝1）等效塑性应变。
图5.4给出了计算得到的宏观RVE中单元高斯点的等效应力－应变曲线，其中考虑损伤的宏观RVE中的等效应力应变是经过对细观RVE的相应物理量与损伤演化耦合计算以后作均匀化处理得到的。对比可以发现，细观RVE中材料塑性、损伤及其演化显著影响着宏观单元的等效应力应变状态，根据不同拉伸状态宏观应力应变曲线可以分为三种阶段：①线弹性阶段0A，所有细观单元应力状态小于其屈服应力，从而显示其宏观材料性能也处于线弹性阶段；②非线性强化阶段AC，在加载点A细观RVE中局部单元出现塑性，发生微小损伤，从而影响到宏观材料性能也跟着降低，随着外部载荷的增加，损伤不断演化，细观损伤区域也不断扩大，从而显示其宏观材料性能处于非线性塑性损伤阶段；③软化阶段BD，随着细观损伤的累积和损伤单元数量增加到某一阶段时，承载能力急剧下降出现软化行为，由此看出均匀化后的等效应力－应变曲线基本上与材料单轴拉伸曲线类似。
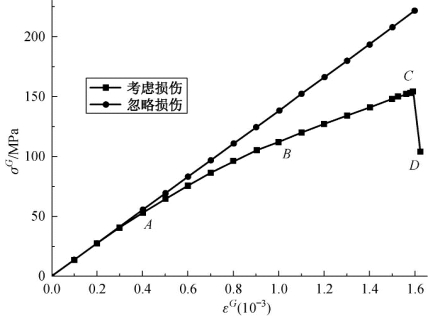
图5.4 考虑局部损伤演化的宏观等效应力与忽略损伤的比较
相关文章
- 详细阅读
-
结构损伤多尺度模拟方法的基本方程详细阅读
以一个任意形状的结构体为例，对嵌套多尺度损伤模拟中的不同尺度域及其边界进行定义和描述。图4.1嵌套多尺度损伤模拟中的尺度域与边界示意图定义结构整体所在的空间为Ω，所属边界为Γ，而Γu和Γτ分别为施加在边界Γ上的已知位移和已知应力。区域ΩGL中的损伤与力学行为需要考虑其在宏观与细观两个尺度下的损伤演化过程方能确定。......
2025-09-30
-
桁架结构多尺度损伤观测方法详细阅读
图2.24桁架局部损伤程度示意图实验中采用扫频试验、电测与光测相结合的方法同步采集结构动力响应与局部损伤过程的信息，实时观测裂纹尖端应变集中、热点应力分布和裂纹萌生与扩展情况，以及结构动力响应参数的变化规律。图2.25桁架结构局部与整体测区位置图2.26局部损伤区测试方案采用上述实验方案在加载的实时同步观测与分析了桁架结构的响应及其焊缝损伤区域的疲劳损伤演化过程。......
2025-09-30
-
一致多尺度方法基本方程-结构损伤多尺度模拟与详细阅读
但是，与图4.1中不同的是，定义结构中含细观缺陷的易损局部所在空间为ΩL，ΓGL表示结构整体区域与细观局部区域交界处。值得注意的是，在嵌套多尺度方法的空间描述中，易损局部域为ΩGL，该区域具有宏观与细观双重尺度属性，而在这里，易损局部域为ΩL，该区域仅具有细观尺度属性。......
2025-09-30
-
结构损伤多尺度模拟-跨尺度界面应力连续方法详细阅读
图4.12纯弯曲作用下跨尺度界面上的应力分布首先假设当跨尺度界面处的梁单元节点只有绕x轴的弯矩Mx作用时，根据界面上大小尺度模型做功相等，可得：其中θx为绕x轴转角。此外，还应注意到，该方法分成四部分导出的跨尺度界......
2025-09-30
-
结构损伤多尺度模拟与分析：实施流程与方法详细阅读
应用本章前3节中阐述的结构损伤多尺度分析的基本方程和计算方法，可进行钢结构地震损伤多尺度分析。关于第1个问题，也即结构损伤一致多尺度分析中的跨尺度界面连接问题，在本章的4.3节已有专门论述。有关如何通过UMAT子程序实现材料损伤特性的引入及其流程的详述将在后面的5.1节给出。......
2025-09-30
-
结构损伤的多尺度模拟与分析详细阅读
因此，结构损伤的量化其实已转化为与特定结构构成和内力分配关系相关的求解过程。对于不同类型的结构，有必要针对其特定的构造形式专门研究其结构损伤的量化方法。......
2025-09-30
-
结构损伤多尺度模拟：数学渐进均匀化方法详细阅读
数学渐进均匀化方法从物理量的数学渐进展开出发，属于多尺度摄动方法范畴，称为数学平均化方法。渐进均匀化方法的基本思想是，在载荷作用下的结构场变量将随着宏观尺度中的坐标点x的变化而变化。这样一来，有必要将上述渐进均匀化方程转换成增量表达形式。......
2025-09-30
相关推荐