混合硬化塑性材料的用户子程序UMAT的代码如下：上面的这个用户子程序UMAT除了背应力张量中的静水压力项不在求解中起作用外，其计算结果与ABAQUS中的线性运动硬化金属塑性材料模型的结果完全相同。这个微小的差异是因为，用户子程序UMAT中使用Prager演化定律来产生偏背应力张量，而ABAQUS中的线性运动硬化金属塑性材料模型则使用Ziegler演化定律，其中包含了流体静水压力对背应力张量的额外贡献。变量statev由ndi个直接分量和nshr个剪切分量组成。......
2023-11-03
UMAT子程序的实施流程：5.1.2详解
【摘要】：在UMAT子程序中实现Lemaitre各向同性损伤本构方程需要重点完成以下三部分内容：分别定义材料塑性和损伤的门槛值及演化规律，准确描述材料的塑性和损伤状态。在UMAT中采用一致切线模量矩阵可以保证ABAQUS主体程序采用的Newton迭代法具有二阶收敛速率，减少增量步结束时由于应变增量微小扰动引起的应力变化。图5.1应用UMAT子程序实现损伤本构描述的流程图
ABAQUS中用户材料子程序UMAT的开发主要解决两方面问题：本构模型建立和积分算法选择。在UMAT中应用完全隐式向后Euler法的径向返回方法，考虑了平衡迭代的收敛和计算结果的正确性，通过编写专门的代码引入材料损伤本构关系，其实施流程如图5.1所示。结构的弹塑性行为与加载以及变形的历史有关，一般使用增量载荷法计算，对每一载荷增量，将弹塑性方程分步线性化，从而使得弹塑性分析这一非线性问题分解为一系列线性问题。弹塑性情况下，线性化处理后的增量形式的材料本构关系可以表示为：
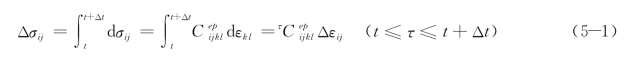
UMAT子程序的主要功能是根据程序定义的材料本构方程，由主程序传入的应变增量求解应力增量，更新积分点处的应力应变状态，提供雅可比矩阵（Jacobian）给ABAQUS主程序以形成下次迭代时的单元切线刚度矩阵和结构整体刚度矩阵。
在UMAT子程序中实现Lemaitre各向同性损伤本构方程需要重点完成以下三部分内容：
（1）分别定义材料塑性和损伤的门槛值及演化规律，准确描述材料的塑性和损伤状态。
在增量形式弹塑性本构方程中，首先调用材料弹性本构关系，计算应力增量预测值及应力预测值，当应力预测值大于屈服应力时，材料进入塑性。由于材料损伤演化和各向同性硬化使得屈服条件不断改变，需要结合该时刻的后继屈服条件、随动强化规律和损伤演化规律来确定材料弹塑性状态和损伤状态。弹塑性状态和损伤状态的决定条件将在下面的5.1.3节中讨论。
（2）选择合适的应力更新算法，根据已有应变增量值和本构方程表达得出应力增量。
准确的应力更新算法可以保证计算结果的精度高，收敛速度快。不合适的算法不仅会导致有误差的应力解，而且会影响平衡迭代的收敛，甚至会导致发散。在本书UMAT子程序中，使用基于完全隐式向后Euler法的径向返回方法，结合非线性方程组的Newton－Raphson迭代过程得到相应的应力增量值。耦合材料损伤的应力更新算法将在5.1.4节中详细讨论。
（3）应用数值算法求解一致切线模量矩阵
。
一致切线模量矩阵又称雅可比矩阵（应力增量对应变增量的变化率矩阵）。材料屈服时，由于突然从弹性状态转变为塑性状态，连续体的弹塑性切线模量可能引起伪加载或卸载。在UMAT中采用一致切线模量矩阵可以保证ABAQUS主体程序采用的Newton迭代法具有二阶收敛速率，减少增量步结束时由于应变增量微小扰动引起的应力变化。关于一致切线模量矩阵的定义与求解，将在5.1.5节中详细给出。
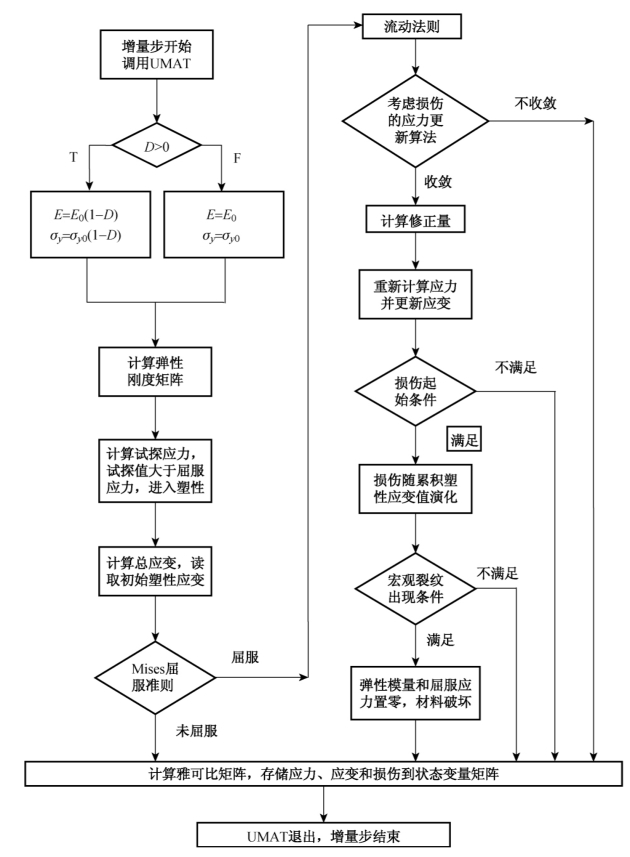
图5.1 应用UMAT子程序实现损伤本构描述的流程图
有关结构损伤多尺度模拟与分析的文章
- 详细阅读
-
基于ABAQUS的UMAT用户材料子程序的C详细阅读
本节将给出一个完整的用C＋＋编写的用户子程序的例子，这是一个简单的线弹性本构模型的用户材料子程序UMAT，其他用Fortran语言编写的用户子程序若要转化为C＋＋编写的用户子程序，也可以仿照这个例子修改用户子程序的接口。C＋＋语言的面向对象的属性在编写大型复杂结构的子程序时具有独特的优势，编写的代码结构更加清晰、可读性更高。......
2023-11-03
-
子程序编程及调用方法详解详细阅读
子程序调用可通过辅助机能M98代码进行，在M98指令中，子程序号由地址P规定。如“N15 M98 P30100；”为调用子程序O0100三次，而“N15 M98 P3100；”则表示调用子程序O3100一次。......
2023-06-25
-
Encounter设计流程详解详细阅读
使用Encounter进行后端物理实现的设计流程如图8.1所示。图8.1 EDI APR流程待布图规划完成后，工具会依据布图规划中的物理约束信息及SDC中的时序约束信息进行布局。如果数目较少，一般通过小范围的改动即可使之满足要求，这种改动称作ECO。DFM包含范围很广，而在APR流程中的DFM主要是进行诸如double via和spread wire width等优化，预防制造过程中由于加工的偏差使得芯片的功能失效。由于本章着重点在EDI的使用，关于此部分内容并不详细展开。......
2023-06-26
-
监理工作流程的规划与实施详细阅读
监理部组建后,按照DL/5111—2000《水电水利工程施工监理规范》建立正常的工作和文件处理程序,明确了处理期限,首先对监理工作进行了规范化管理。对于每一道工序进行“三检”,并将“三检”结果送交监理工程师,并经签字认可后,方可进行下道工序的施工。施工当中各类报表根据各监理单位规定按时报送。现场出现质量和安全事故,承建单位应及时上报,任何质量事故(缺陷)和安全事故均不得隐瞒监理工程师而自行处理。......
2023-06-21
-
CalibrePEX流程详解举例详细阅读
本节采用内嵌在Cadence Virtuoso Layout Editor的菜单选项来启动Calibre PEX。图4.100 打开Miller_OTA版图4）打开Calibre PEX工具。图4.107 Calibre LVS结果查看图形界面11）在Calibre PEX运行后，同时会弹出参数提取后的主网表，如图4.108所示，此网表可以在HSPICE软件中进行后仿真。图4.108 Calibre PEX提出部分的主网表示意图以上就完成了Calibre PEX寄生参数提取的流程。......
2023-06-26
-
实施步骤与要求详解详细阅读
最后将元件全部放进PCB框内，如图5-32所示。布局时应充分考虑PCB的实用性，比如电源端口、数据端口和信号端口等应布局到PCB的边沿。图5-33 PCB布局图PCB完成大致布局后需要按设计要求进行PCB规则设置，如图5-34所示。......
2023-06-23
-
if语句执行流程：条件判断和执行流程详解详细阅读
图6.2.1if语句执行流程6.2.1.html根据两个变量的大小关系，使用if条件语句输出对应提示，如下所示。图6.2.2if语句if语句中的表达式布尔值为true，执行语句console.log;，执行完成之后继续执行console.log; 。◇ 表达式expression布尔值为false时，执行语句secondStatement。◇ 支持加入多个else if条件语句。if语句的其他限制：◇ if语句是必选项，else if和else语句是可选项。......
2023-11-08
相关推荐