结构损伤一致多尺度分析的关键是在不同尺度的模型衔接起来进行计算，为此首先需要将前述跨尺度界面单元衔接方法引入ABAQUS，按软件指定的格式引入跨尺度界面上须满足的位移约束方程。但是由于K2本身是奇异的，同时计算机有效位数是有限的，α过大会导致系统方程病态而使计算失效。根据所建立的结构一致多尺度模型并通过宏细观变量的跨尺度关联，便可实现结构损伤的并发多尺度计算。......
2023-08-26
结构损伤量化方法与多尺度模拟分析
【摘要】：以如图3.35所示的多根杆件铰接的结构为例，说明铰接结构的损伤量化方法。构件层次损伤为。图3.37单层单跨刚性连接框架结构则框架的水平位移其中积分号表示沿构件长度方向积分，则该框架结构的侧向刚度为若考虑各构件中的损伤导致的界面抗弯刚度折减，则其有效刚度为则即为该框架结构的损伤表达式。
钢架结构通常包括杆系结构、框架结构和桁架结构，各构件之间的连接方式通常包括铰接和刚接。这里以铰性连接结构和刚性连接结构为例，推导其结构损伤量化公式。
1.铰性连接结构损伤量化
铰性连接结构的特点在于其中的内力只有轴力，且轴力沿构件长度方向为常数；各构件的连接节点不能传递弯矩，但是可以产生连接夹角变形。
以如图3.35所示的多根杆件铰接的结构为例，说明铰接结构的损伤量化方法。该结构中各构件长度均为l，抗拉刚度为EiAi，当结构跨中作用竖向向下的集中力F时，各构件内力分布如图3.35中所示。构件层次损伤为
。
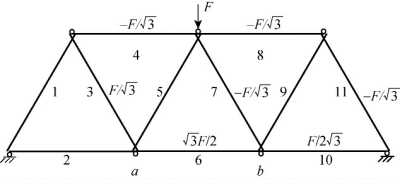
图3.35 多杆铰性连接结构及其杆件内力分布
根据变形体系虚功原理，在a点施加单位荷载，求解得到对应的内力分布如图3.36所示。
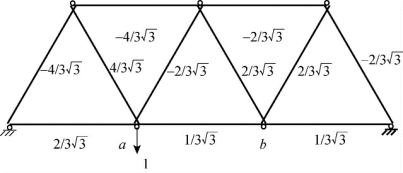
图3.36 单位荷载作用下杆件内力分布
据结构力学位移计算公式，得到a点挠度：
其中：
——a点作用单位集中力时，第i个构件内力，i＝1，2，…，11；
Fi——集中力F作用下，第i个构件内力，i＝1，2，…，11。
根据图3.35中的内力分布，假设Fi＝φiF，其中，φi设为内力分配系数，并且该系数仅与各构件的构成关系有关，与材料属性及构件尺寸无关。则式（3－102）可转化为：
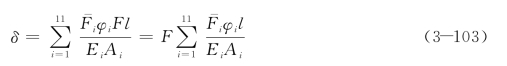
由此得到结构的刚度计算公式：
考虑各构件的损伤，则式（3－104）转化为：
综合式（3－104）、式（3－105），并假设各构件截面抗拉刚度相同均为EA，可得：
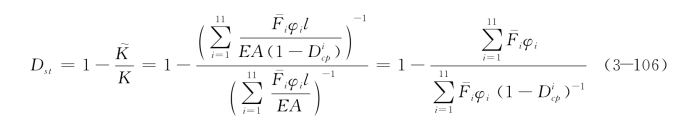
式（3－106）即为铰性连接静定结构损伤量化公式。其中，结构损伤变量由各构件的损伤变量以及各构件内力分配系数来决定。
2.刚性连接结构损伤量化
对于刚性连接结构，弯矩是结构变形的主要因素，轴力和剪力对其变形的影响较小。以图3.37中的单层单跨刚性连接超静定结构为例，结构中的柱高h，梁长l，柱和梁的抗弯刚度分别为E1I1、E2I2，在左侧柱端作用水平力F，结构右侧柱端产生侧向位移δ。
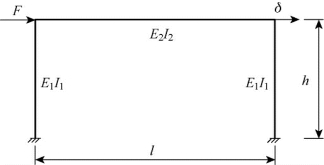
图3.37 单层单跨刚性连接框架结构
则框架的水平位移
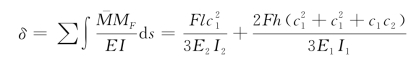
其中积分号表示沿构件长度方向积分，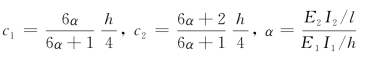
则该框架结构的侧向刚度为
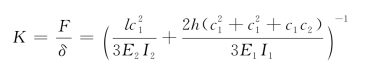
若考虑各构件中的损伤导致的界面抗弯刚度折减，则其有效刚度为
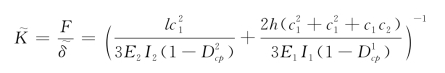
则
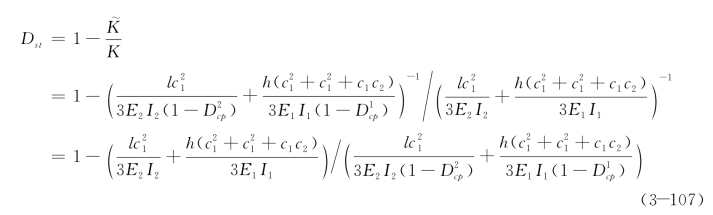
即为该框架结构的损伤表达式。若E1I1＝E2I2＝EI，则上式可简化为
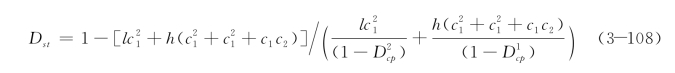
对于多层框架结构，可借助专业结构分析软件计算得到外荷载以及单位荷载作用下各构件内力分布和弯矩图，再根据结构损伤位移计算公式建立位移与荷载的关系，得到相应的结构整体刚度和各构件抗弯刚度的关系式，再进行与上述类似的推导，即可得到复杂框架结构损伤表达式。
3.动力效应对结构损伤量化的影响
在前述的损伤量化公式推导过程中，未考虑动荷载对于损伤演化的影响。当结构承受的动荷载的动力效应比较显著时，则需考虑动力效应对结构损伤演化的影响。这里以图3.38所示中的单层刚性连接框架结构为例进行分析。
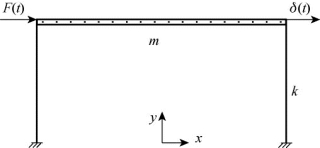
图3.38 动荷载作用下的单层刚性连接框架结构
单层刚性连接框架结构可简化为一质量－刚度系统，如图3.38所示，在框架梁上施加简谐力F（t）＝Fpsinωpt，对应的稳定位移响应为δ（t），则该单自由度系统的振动微分方程为：
求解该方程，得到平稳阶段振动位移为：
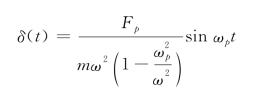
其中，ω2＝k／m为结构自振固有频率，则上式可转化为：
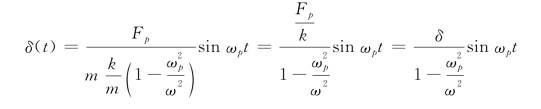
其中，δ为在静载Fp作用下结构静位移，而最大动位移和最大静位移的比值，即动力系数β为：
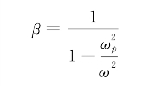
对应的，该结构的动刚度为βk；此时，考虑材料体元与构件体元损伤对于结构整体刚度的影响，得到结构的有效刚度为：
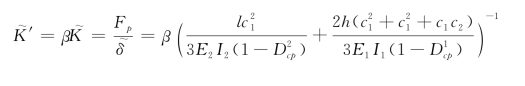
结构损伤为：
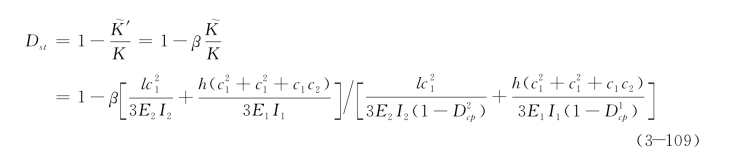
将式（3－109）与式（3－110）比较分析动力系数β的作用：
（1）当ωp／ω→0时，β→1，这时荷载的数值虽然随时间变化，但其对结构位移响应的影响较小，可当做静荷载处理；
（2）当0＜ωp／ω＜1时，β＞1，且β随ωp／ω的增大而增大，动力效应对结构损伤存在影响；
（3）当ωp／ω→1时，｜β｜→∞，振幅无限增大，动力效应的影响较明显；
（4）当ωp／ω＞1时，且β随ωp／ω的增大而减小，动力效应的影响逐渐减弱。
以上分析了在动荷载作用下结构位移随ωp／ω的变化趋势，结构内力也存在类似的规律，因此可用于结构动荷载作用下的动力效应和损伤分析。
对于两层刚性连接框架结构，假设在底层横梁上作用荷载F（t）＝Fpsinωpt，如图3.39所示，其刚度系数分别为：
根据其振动方程：
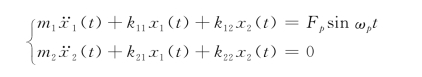
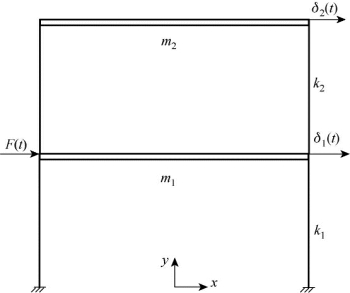
图3.39 动荷载作用下两层刚性连接框架结构
令m1＝m2＝m，k1＝k2＝k，求解上述方程组，得到平稳阶段振动位移：
其中，
。而动力系数β1、β2的表达式更加复杂，二者均与激励频率和结构的两阶固有频率有关，并且结构存在两个共振频率。因此，该情况下的结构损伤除了具有与单层框架结构类似的规律以外，还需考虑上层“附加质量和刚度”的影响，例如，当
时，δ1（t）＝0，δ2（t）＝－Fpsinωpt／k2，这意味着下层结构的振动被消除，同时｜β2｜＝1，上层结构相当于处于静荷载作用，可根据公式（3－109）求得损伤。而对于其他多自由度振动体系，可根据荷载条件建立其振动方程，求解其振动位移响应，并根据实际条件具体分析得到其损伤量化公式。
有关结构损伤多尺度模拟与分析的文章
- 详细阅读
-
结构损伤多尺度模拟与分析详细阅读
对这些易损部位就需要考虑材料与结构在细观尺度下存在的细观缺陷及其非连续、非均匀特征进行损伤分析，在这些易损局部的复杂几何构造细节和在内部客观存在的细观缺陷，导致局部热点应力升高、触发损伤演化。分析其组成材料的性能、含量、界面、缺陷等，基于对这些细观构造与缺陷的细观分析结果来确定这些易损部位在宏观尺度下结构模型中的近似于均匀材料的等效性能。......
2023-08-26
-
结构损伤多尺度模拟与分析：实施流程与方法详细阅读
应用本章前3节中阐述的结构损伤多尺度分析的基本方程和计算方法，可进行钢结构地震损伤多尺度分析。关于第1个问题，也即结构损伤一致多尺度分析中的跨尺度界面连接问题，在本章的4.3节已有专门论述。有关如何通过UMAT子程序实现材料损伤特性的引入及其流程的详述将在后面的5.1节给出。......
2023-08-26
-
结构损伤多尺度模拟与分析验证详细阅读
在考虑材料损伤演化与失效过程的有限元分析中，损伤演化方程与结构平衡方程、几何方程、物理方程一起，构成基本方程组。目前耦合损伤的有限元计算方法主要有：全解耦方法。本章在上一章对两种多尺度方法基本理论介绍的基础上，分别阐述了两种多尺度分析方法在有限元计算软件ABAQUS中实施的算法流程与具体步骤，并通过算例分析以验证两种损伤多尺度分析方法各自的有效性和可行性。......
2023-08-26
-
结构损伤多尺度模拟与分析：混凝土损伤特征与演详细阅读
构件受力后，钢筋和混凝土之间有相对滑移趋势时，产生摩阻力。这个过程就是钢筋混凝土粘结界面的损伤演化过程。现行钢混结构设计理论大多是基于平截面假定进行的，这隐含着钢筋和混凝土这两种性质截然不同的材料粘结良好，以确保二者变形协调。保障钢筋和混凝土的粘结良好是确保钢混结构安全的重要条件之一。图2.44钢筋与混凝土粘结失效引发的结构破坏......
2023-08-26
-
结构损伤的多尺度模拟与分析详细阅读
因此，结构损伤的量化其实已转化为与特定结构构成和内力分配关系相关的求解过程。对于不同类型的结构，有必要针对其特定的构造形式专门研究其结构损伤的量化方法。......
2023-08-26
-
一致多尺度方法基本方程-结构损伤多尺度模拟与详细阅读
但是，与图4.1中不同的是，定义结构中含细观缺陷的易损局部所在空间为ΩL，ΓGL表示结构整体区域与细观局部区域交界处。值得注意的是，在嵌套多尺度方法的空间描述中，易损局部域为ΩGL，该区域具有宏观与细观双重尺度属性，而在这里，易损局部域为ΩL，该区域仅具有细观尺度属性。......
2023-08-26
-
结构损伤多尺度模拟方法的基本方程详细阅读
以一个任意形状的结构体为例，对嵌套多尺度损伤模拟中的不同尺度域及其边界进行定义和描述。图4.1嵌套多尺度损伤模拟中的尺度域与边界示意图定义结构整体所在的空间为Ω，所属边界为Γ，而Γu和Γτ分别为施加在边界Γ上的已知位移和已知应力。区域ΩGL中的损伤与力学行为需要考虑其在宏观与细观两个尺度下的损伤演化过程方能确定。......
2023-08-26
相关推荐