典型钢筋混凝土框架结构的损伤量化分析

钢筋混凝土框架房屋是工业与民用建筑中常用的结构形式，这里就以一个三层钢筋混凝土框架结构为例，考察基于损伤附加应变能的耗能型损伤表征量化方法的可靠性。

1.钢筋混凝土框架结构分析案例

如图3.23所示钢筋混凝土框架结构，框架柱截面尺寸为400mm×400mm，配筋率为1.5%；框架梁截面尺寸为500mm×250mm配筋率如图3.23所示。根据给出的配筋率和截面尺寸，选择典型梁、柱构件进行有限元建模分析，框架柱截面尺寸为400mm×400mm，配12根直径为16mm的主筋，箍筋选择φ8＠100；框架梁截面尺寸为500mm×250mm，底部配3根直径为22 mm的主筋，中部配2根直径为18 mm的腰筋，顶部配2根直径为18mm的通常筋，箍筋选择φ8＠100。混凝土选用C30，钢筋主筋HRB 400（E＝206GPa，μ＝0.3，σy＝400MPa），箍筋HPB 235（E＝206GPa，μ＝0.3，σy＝235MPa）。分别对该结构施加顶点水平位移荷载以及如图3.24所示El－Centro地震波作用。

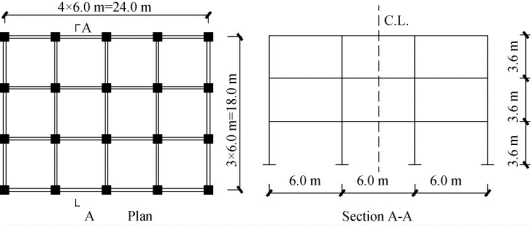
图3.23　三层框架结构的平、立面布置图

计算中将混凝土受压应力－应变关系分为直线上升段、曲线上升段和曲线下降段三个阶段来模拟，三个阶段的应力－应变关系分别表示为：

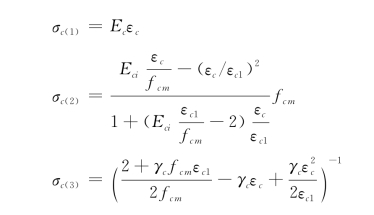
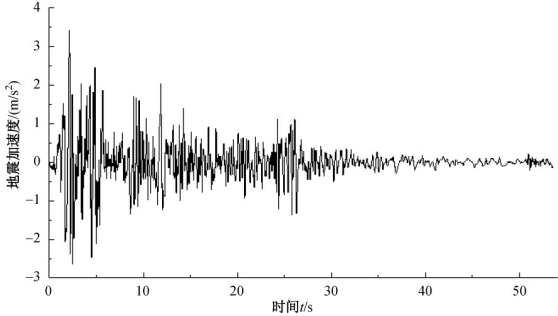
图3.24　地震加速度谱

上述应力－应变关系的前两部分描述了应力从起始到应变为εc1时达峰值fcm的过程，第三部分描述了曲线下降段。为了确保独立的网格划分能有较好的仿真结果，考虑了对试样几何形状的影响。因此，σc（3）的计算中包含了的递减函数γc，作为材料属性的常数－破碎能Gcl和由于结构网格划分导致的一个内部长度的参数lc。有关计算中所采用的混凝土损伤本构关系及其参数确定的更多阐述，有兴趣的读者可以参考文献［22］。

单轴压缩时的损伤因子dc的演化由与之相应的塑性应变通过实验确定的常数bc（0＜bc＜1）决定与非弹性应变成正比。

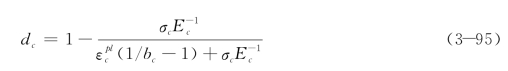
单轴拉伸的应力－应变关系σt（εt）由一个强度从初始上升至fct的线性部分和一个依赖于几何形状的非线性递减部分组成。

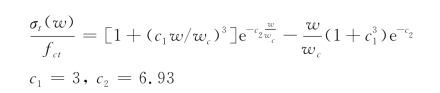
用非弹性应变和内部长度参数lt取代裂缝宽度w，得到

σt（εt）包含了断裂能GF和lt的比值。

类似于单轴压缩的状况，单轴拉伸的损伤因子dt取决于和bt。

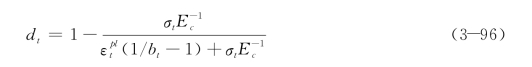
2.结构损伤量化分析公式

（1）结构失效所需能量UFE的确定

根据上述结构模型及加载方式，该钢混结构及构件失效能量的计算采用可UFE＝Fy（δu－δy）。其中Fy，δy，δu分别为结构和构件极限荷载、屈服以及破坏时对应的位移。对于结构失效能量的近似计算除了采用这种百分比的方法，还有能量等效方法等。

其中，对于单试件在单调加载下的极限位移，可采用《钢筋混凝土建筑基于位移的抗震设计》研究报告以1 282个钢筋混凝土构件的试验结果回归出经验公式［23］来计算：

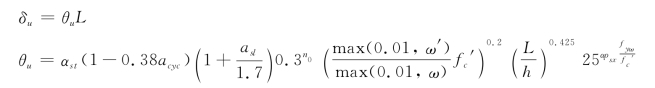
其中涉及的参数比较多，有兴趣的读者可参考文献［22］，这里不一一列举。

（2）结构损伤附加应变能的计算

对于本算例采用的混凝土损伤塑性模型及参数，当结构构件发生损伤时，将由于损伤引起的附加应变能记为UDIE：

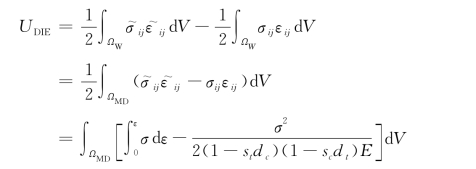
其中dc和dt的取值分别采用公式（3－95）和公式（3－96）来计算。

3.结构中的梁、柱构件损伤量化分析

（1）单次加载下钢筋混凝土梁、柱损伤计算分析

根据相关研究报告给出的经验公式，初步估算在该案例结构中的梁和柱的极限位移分别是182.15mm和155.48mm，有限元分析时梁和柱的加载位移均选择200mm，得到梁、柱构件的荷载－位移曲线如图3.25所示。

然后根据该图数据分别计算梁和柱的屈服位移、极限位移及失效能量UFE。由此得到的钢筋混凝土柱的有限元计算结果为：

δy＝23.93mm，δu＝188.66mm，Fy＝159.51kN，

UFE＝Fy（δu－δy）＝159.51kN×（188.66－23.93）mm＝26.28kN·m。

钢筋混凝土梁的计算结果为：

δy＝52.16mm，δu＝199.86mm，Fy＝102.20kN，

UFE＝Fy（δu－δy）＝102.20kN×（199.86－52.16）mm＝15.09kN·m。

从以上结果可以看出，有限元模拟结果与试验得到的经验公式计算结果基本吻合，下面将结合有限元实际计算损伤结果分别对梁柱构件及框架结构在单次加载情形及不同强度的地震荷载作用下的各种工程结构损伤指标进行比较，说明损伤耗能量化方法在结构完整性评估应用中的优势与局限。

首先通过梁、柱构件在不同位移荷载工况下材料损伤云图对梁、柱构件损伤演化过程有一个定性的了解，并结合图3.25用以分析比较各种工程结构损伤指标的合理性与有效性。图3.26和图3.27分别是典型柱和梁构件在不同的位移荷载工况下的材料拉伸损伤云图，显示了梁柱构件在单次加载过程中材料损伤的累积与演化，其中（a）～（i）／（l）分别对应图3.25中标示的各荷载工况，柱子（a）～（i）分别对应的位移荷载为10，20，30，40，50，77，91，100，200mm，梁（a）～（l）分别对应位移荷载10，20，30，40，50，60，70，80，90，100，130，200mm。

图3.25　梁、柱构件荷载－位移曲线

图3.26　不同位移荷载工况下柱拉伸损伤云图（彩图见附录）

从图3.26和图3.27中可以看出，在很小的位移荷载下（δ＜10mm）梁柱构件受拉区便发生材料损伤，但此时发生损伤的区域还较小，对结构整体的服役性能影响不大，此时构件整体上还处于“线弹性”工作状态。这里的线弹性之所以加引号表示是因为实际上此时结构已经发生了损伤，结构在屈服之前的“线弹性”阶段的切线刚度并非是结构无损时线弹性刚度，从图3.25中可以看出，此时结构名义刚度明显大于结构屈服前的切线刚度，图中还可看出梁、柱构件实际屈服位移在30mm和50mm左右，在结构开始承载到屈服便处于“线弹性”工作状态。从有限元计算结果观察钢筋在承载过程中的应力变化，发现柱和梁底部钢筋分别在20mm及51.49mm的荷载工况下开始进入屈服阶段。在这一“线弹性”阶段混凝土受拉损伤区随荷载增大逐渐扩展，并随着钢筋进入屈服阶段逐渐发展并趋于稳定，整个过程中柱底承载面积逐渐减少直至破坏。

图3.27　不同位移荷载工况下梁拉伸损伤云图（彩图见附录）

（2）耗能损伤量化分析结果与工程损伤指标的比较

在对梁柱构件单调加载情形下损伤的累积和演化有一个定性认识的基础上，进一步计算此过程中不同荷载工况下常见结构构件工程结构损伤指标的变化。图3.28和图3.29分别是典型框架柱和梁构件在单调加载下不同荷载工况时常见损伤量化指标与本书损伤耗能量化指标的变化过程及比较。图中用以比较的各工程结构损伤指标分别为：

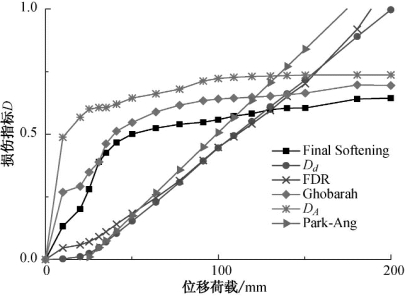
图3.28　框架柱在单调加载下不同荷载工况时各损伤指标的比较

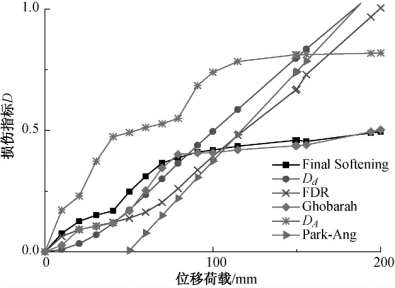
图3.29　框架梁在单调加载下不同荷载工况时各损伤指标比较

Final Softening——最终软化指标；

FDR——柔性损伤指标；

Ghobarah——刚度损伤指标；

DA——构件底部材料受拉损伤指标；

Park－Ang——变形－能量双参数损伤指标，该指标在结构损伤初期损伤值为负值，与结构损伤定义不符，在此处以及后文中一致予以截断；

Dd——损伤耗能量化指标。

从图3.28和图3.29可以看出，几种工程结构损伤指标的变化趋势可以分成两类：最终软化指标及Ghobarah刚度损伤指标与构件底部材料受拉损伤指标DA的变化趋势相一致；基于刚度退化率的柔性损伤指标及考虑变形和能量共同影响的Park－Ang与损伤耗能量化损伤指标变化趋势相一致。最终软化损伤指标作为典型的基于结构动态响应的指标，其核心思想是结构动力响应指标是损伤引起结构刚度的直接体现，反映的是结构整体刚度的下降，而Ghobarah的损伤指标也是基于结构抗侧移刚度的下降，所以这两个指标相一致的变化趋势也在合理的预期之中。同时，分析中采用的混凝土材料的损伤本构中对于损伤的定义也是基于弹性模量的下降，而刚度可以看成是各点材料弹性模量在体域内的积分，所以DA与最终软化指标及Ghobarah刚度指标变化趋势的一致性也合情合理。Park－Ang指标中由于考虑了位移的影响，在构件损伤初期的“线弹性”阶段里，损伤值并不为零；同时由于考虑了累积耗能的影响，在构件失效时的损伤值也大于1。

对于钢混构件而言，前一类工程结构损伤指标对于结构损伤初期局部材料损伤较为敏感，因此在构件局部产生损伤时便能给出预警与指示；但在结构损伤初期，结构整体还处于“线弹性”服役阶段，用这一类指标显然高估了结构整体的损伤程度，对于结构完整度的评估过于悲观；同时该算例中这类工程结构损伤指标在构件进入屈服阶段到构件失效的过程中仅从0.2左右变化到0.5左右，在损伤长期累积和发展的过程中变化范围仅为0.3左右，显然对于整个损伤过程的评估来说是不利的，尤其是用于对损伤结构的预后分析更是致命的缺憾。第二类工程结构损伤指标在整个过程中变化趋势比较平稳，在“线弹性”阶段指示损伤较小，损伤指标变化也比较平缓，在进入塑性阶段后损伤的累积相对于“线弹性”阶段加快，到构件失效时这类工程结构损伤指标维持在1左右。

4.地震作用下钢筋混凝土框架结构损伤量化分析

图3.30是计算得到的该框架结构在地震作用（以地面运动加速度峰值PGA＝0.2g为例）的不同阶段的结构损伤云图，从中可以看出在t＝1.806s时结构中有局部产生损伤，并在此后t＝1.806～3s的时间段内结构损伤在柱底及框架梁柱节点处迅速累积，在这之后到地震结束损伤累积缓慢，损伤分布云图变化不大。整个过程中在t＝3s左右损伤累积最快，参考地震加速度谱，此时对应的正是地震加速度最大的时刻，在此后虽然也有较大幅度的地震加速度作用，但是损伤的累积并不大。这种损伤累积的特征也反映在框架顶部位移及层间位移角的变化上。

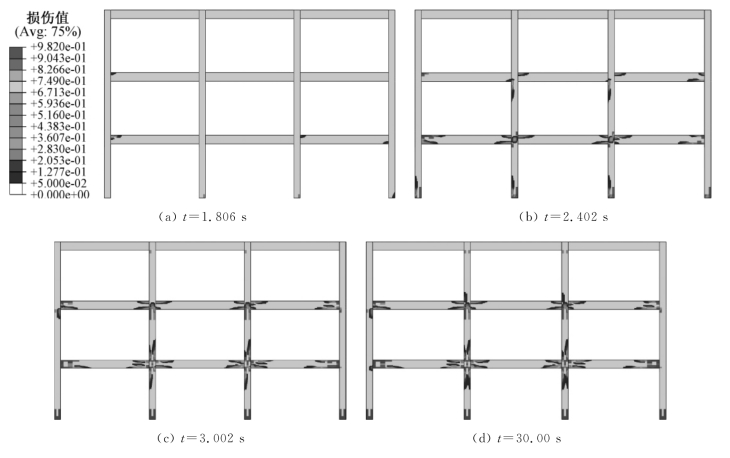
图3.30　地震作用（PGA＝0.2g）下结构损伤演化不同阶段材料损伤云图（彩图见附录）

计算结果表明，地震荷载下结构构件的损伤是一个逐步累积的过程，除了受地震加速度幅值的影响，还受到地震持时的影响。地震持时越长，结构损伤累积程度越高，同样幅值的加速度荷载越有可能引起结构宏观服役性能的变化。损伤耗能量变化趋势与框架结构底部材料损伤亦即框架结构柱底承载面积损失的变化趋势相一致，说明损伤耗能量化方法能够反映结构构件局部损伤的累积程度；同时该结果与之前对于结构整体层间位移的发展趋势相符合，同时也能反映结构整体服役性能的下降。损伤耗能量在t＝3s左右增长较快且增幅较大，反映了地震加速度幅值对于结构损伤的影响，同时损伤耗能在t＝15s及28s处有小幅度的增长，在一定程度反映了地震持时对结构损伤的影响。

结构耗能损伤量化分析结果与工程损伤指标的比较：

对该框架结构作用不同加速度峰值的El－Centro地震波作用，分别取PGA＝0.05g、0.10g、0.15g以及0.20g以模拟不同程度的结构地震损伤。计算所得该框架结构在不同加速度峰值的El－Centro地震波作用下震后结构损伤分布云图如3.31所示。

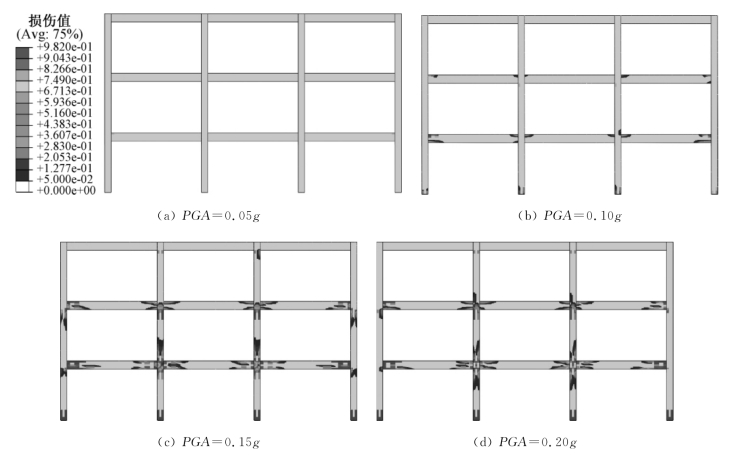
图3.31　不同强度地震震后结构损伤云图（彩图见附录）

将不同加速度峰值的地震作用下损伤耗能量化分析结果与工程损伤指标的计算结果进行分析比较，如图3.32所示。

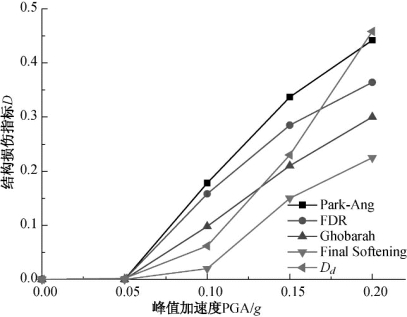
图3.32　不同加速度峰值的地震作用下结构损伤指标比较

从图3.32依然可以看出最终软化损伤指标与Ghobarah刚度指标变化趋势的相似性，这是由于在众多指标中两者概念的相似性决定的，同样的这两者用于表征结构整体的损伤时指示的损伤偏小。而由于FDR损伤指标在理想弹塑性下退化成Park－Ang指标中的位移项，两者相似的变化趋势在本算例中也得到了体现。在该算例中，损伤耗能量化结果能够体现结构中发生的小损伤，同时对于大的结构损伤的区别度较其他损伤指标更好，并且呈现非线性的变化趋势。

5.损伤耗能表征和量化方法用于结构损伤分析的优势与局限

从以上分析中可以看出，用于参考和比较的工程结构损伤指标的变化趋势可以分成两类：最终软化损伤指标及Ghobarah刚度损伤指标与构件底部材料受拉损伤指标DA的变化趋势相一致；基于刚度退化率的柔性损伤指标及考虑变形和能量共同影响的Park－Ang与损伤耗能量化指标变化趋势相一致。这种一致性的内在原因在于：最终软化损伤指标作为典型的基于结构动态响应的指标，反映的是结构整体刚度的下降，而Ghobarah的刚度损伤指标也是基于结构抗侧移刚度的下降，因此这两个指标在抗侧移框架结构和构件的损伤分析中变化趋势始终一致；对于混凝土材料损伤塑性本构中基于弹性模量的下降定义的损伤DA，由于结构加载机制的特殊性，而刚度可以看成是各点材料弹性模量在体域内的积分，所以DA与最终软化损伤指标及Ghobarah刚度指标在变化趋势上的一致性；基于刚度退化率的柔性损伤指标FDR在理想弹塑性情形下与Park－Ang指标中位移项相一致。根据有限元计算的该框架结构典型梁、柱构件的荷载位移曲线，该加载模式下的梁柱构件也可以非常粗略地近似为理想弹塑性，因此两者的变化趋势也相差不大。

这两类指标各有其优势和局限：在水平侧移加载模式下，由于柱底抗拉混凝土的失效导致结构损伤初期承载面积的丧失，考虑到刚度是构件局部刚度的累加，导致前一类指标在应用于构件层次损伤表征的效果较结构层次要好，且对于结构损伤初期局部材料损伤较为敏感，因此在构件局部产生损伤时便能给出预警与指示；这两个指标的优势还体现在其计算以及测量的便捷性上。

但同时根据对损伤过程的分析，在结构服役初期，只有很少局部发生损伤，结构整体还处于“线弹性”变形阶段，用这一类指标显然高估了结构整体的损伤程度，对于结构完整度的评估过于悲观；而对应于构件和结构损伤的演化过程，这两个指标在结构损伤演化后期变化平缓，在构件进入屈服阶段到构件失效的过程中仅从0.2左右变化到0.5左右，在损伤长期累积和发展的过程中变化范围仅为0.3左右，在构件失效时这类损伤指标指示损伤为0.5左右，而在结构失效时，更是只有0.1左右；说明这两个指标对于结构初期损伤的判断过于悲观，而对于结构中后期严重损伤的评估又过于乐观。显然对于整个损伤过程的评估来说是不利的，尤其是用于对损伤结构的预后分析更是致命的缺陷。

上述结论虽然很大程度上与案例分析中选择的加载模式相关，但是考虑到这两个指标在损伤到失效整个过程中变化范围小，在整个结构服役期内变化趋势平缓，因此这两个指标更适合作为构件局部的损伤指标。

第二类指标较第一类指标而言在结构损伤的初始阶段指示的损伤值虽然小，但是也能反映结构损伤的存在；这一类指标在整个过程中变化趋势比较平稳，在进入塑性阶段后损伤的累积相对于“线弹性”阶段加快，在结构失效时稳定在1左右；在结构服役到失效的过程中损伤指标的变化范围从0到1，能够表征结构损伤的各个阶段，适合用作结构整体损伤程度的评估和结构预后分析。其缺陷在于对于结构损伤初期的损伤判断有一定的可疑性。例如Park－Ang指标中由于考虑了位移的影响，在构件损伤初期的“线弹性”阶段里，损伤值并不为零；同时由于考虑了累积耗能的影响，在构件失效时的损伤值也大于1。除此之外，这一类损伤指标还依赖于各加载模式下结构失效模式及失效状态的判定。

损伤耗能量化指标便是属于第二类损伤指标。由于该指标是基于能量耗散的指标，所以在结构损伤初期该指标为0，克服了部分第二类损伤指标在结构未损伤的线弹性阶段不为0的缺陷；且由于能量耗散的不可逆性，该损伤指标符合损伤指标单调性要求；从案例计算分析可以看出，该损伤指标与第二类损伤指标的变化趋势相一致，且与结构构件局部的损伤指标变化有一定的相关性，应用于结构地震损伤分析时能够反映加速度幅值的对结构损伤的贡献，也能一定程度上体现地震持时的作用。该指标的局限在于其可靠性很大程度上依赖于结构失效模式及失效临界状态的准确判定，而对于结构失效模式及临界状态的判定本身其实是一个复杂的命题。此外，对于复杂的钢混结构，由于混凝土损伤本构关系的复杂性和损伤演化与结构响应的耦合作用，想要得到确定的损伤附加应变能的表达式是很困难的，需要通过数值方法去求解。