分形维数可对此类自相似现象的整体特性提供数学描述。分形研究的对象是具有不规则性和自相似性的无序系统，定量描述这种自相似性的参数是分形维数，分形维数的变化是连续的。可以用分形维数来表征广泛存在于自然界的一类无序、复杂、奇异客体。......
2025-09-30
结构损伤多尺度模拟：裂纹扩展准则3.4.2
【摘要】：图3.15疲劳裂纹扩展速率分区图3.15中I区的特性是存在一个“疲劳门槛”，即循环应力强度因子幅值ΔKth，在该区内应力强度因子幅值低于门槛值，疲劳裂纹基本不扩展。在高速率区，疲劳裂纹k扩展速率较快，出于简化计算和突出对II区的研究，认为裂纹扩展速率恒为，进入高速率区的判断准则为该裂纹的应力强度因子幅值ΔKth，J＞0.8 KC，J。
主要考虑两种工程中常见荷载工况下的裂纹扩展准则，一是准静态加载，另一是疲劳荷载。准静态加载导致的破坏是由材料达到强度后不能抵挡所施加的静态荷载而导致的；而疲劳是在低于或者远低于强度的荷载循环作用下，材料中的疲劳裂纹萌生和不断扩展导致的破坏，两种情况具有不同的损伤与失效机理。
1.准静态裂纹扩展准则
在准静态荷载下，裂纹扩展的驱动力为应力强度因子。根据线弹性断裂力学理论，当裂纹尖端的应力强度因子达到断裂韧度时发生裂纹扩展，即裂纹扩展的准则是：
这里KI为I型裂纹的应力强度因子，KI，C为I型断裂韧度。
基于上述准则，任意扩展步后计算得到所有裂纹尖端的应力强度因子，其中第J条裂纹的I型（拉伸）和II型（剪切）应力强度因子为
。那么第J条裂纹的等效应力强度因子可以计算为：
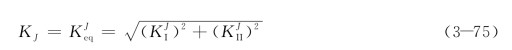
其裂纹扩展准则为：
这里KC，J为第J条裂纹尖端的断裂韧度（toughness），根据下面不同情况选取不同值：
（1）在界面上：KC，J＝KC，interface
（2）在砂浆中：KC，J＝KC，mortar
在每一步分析中，首先施加测试载荷F0或d0（分别对应于应力控制和位移控制的边界条件）。求解该问题可以获得所有裂纹尖端的应力强度因子KJ，然后确定“危险”（即处于扩展临界状态）的裂纹尖端，β为接近断裂韧度的裂纹，即
这里Ntips为所有裂纹尖端总数。
具有“危险”的裂纹J的扩展方向由以下方法确定：
（1）若尖端位于界面上，裂纹将沿着界面扩展，迅速地扩展到长轴的两端。在后面的计算步中，裂纹将被视为一般裂纹，即断裂韧度取为KC，mortar。
（2）若尖端位于砂浆，裂纹将往指定方向扩展Δl长度，扩展方向由最大周向拉应力原则确定，即
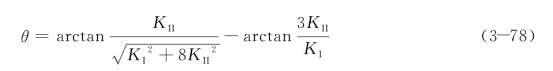(https://www.chuimin.cn)
2.疲劳裂纹扩展准则
疲劳荷载下的裂纹扩展规律由Paris提出，建立了应力强度因子和裂纹扩展速率之间的关系，是当今工程中应用广泛的疲劳裂纹扩展理论：
其中a为裂纹长度，da／dN为裂纹扩展速率，C、m为材料常数，可由实验数据拟合得到，ΔK为应力强度因子幅值。
疲劳裂纹扩展的三阶段理论引入了疲劳扩展的应力强度因子门槛值ΔKth，认为低于此门槛时裂纹不扩展。疲劳裂纹扩展的三个阶段（区）如图3.15所示。
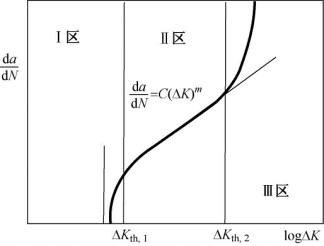
图3.15 疲劳裂纹扩展速率分区
图3.15中I区的特性是存在一个“疲劳门槛”，即循环应力强度因子幅值ΔKth，在该区内应力强度因子幅值低于门槛值，疲劳裂纹基本不扩展。II区为应力强度因子幅值大于ΔKth的疲劳裂纹扩展特性，在该区内的裂纹扩展速率da／dN与应力强度因子幅值ΔK的关系服从Paris公式。在III区，ΔKmax已经接近材料的断裂韧度KI，C，裂纹扩展速率将呈失稳状态急剧增快直至迅速断裂。
实验研究［17］表明，混凝土的裂纹扩展与加载的频率相关，当加载频率较低时，混凝土构件裂纹长度也会像金属材料那样随着疲劳荷载次数的增加而缓慢增加，并且扩展速率也服从Paris公式。根据上述理论，对于疲劳荷载，可引入以下的裂纹扩展率计算方式：
（1）在低速率区（I区），疲劳裂纹扩展速率很低，认为裂纹不发生扩展，该裂纹的扩展门槛值ΔKth，J＝0.2 KC，J。其中J表示不同的裂纹，KC，J为该条裂纹的断裂韧度。
（2）在中速率区（II区），认为裂纹扩展速率符合满足Paris公式：
其中混凝土材料参数C、m的选取参考文献［17］的实验数据，m取值一般为1.0～2.5之间，裂纹扩展速率一般在10－5 mm／c与10－2 mm／c之间。
（3）在高速率区（III区），疲劳裂纹k扩展速率较快，出于简化计算和突出对II区的研究，认为裂纹扩展速率恒为
，进入高速率区的判断准则为该裂纹的应力强度因子幅值ΔKth，J＞0.8 KC，J。
需要说明的是，实际计算过程中，一个计算步不等于一个荷载循环步。疲劳模拟中不会把每一次荷载循环都逐个计算，这会导致计算效率很低，实际上，荷载只有循环到一定次数之后，裂纹才出现明显的扩展。因此，计算中实行的是控制Δa策略，即
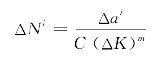
在每一个“计算步”（记为i上标，以区别于表示裂纹的下标J）中，控制裂纹扩展速率最大的那个裂纹（记为β）所扩展的长度为Δai，然后计算出ΔNi，然后遍历所有的裂纹，计算裂纹扩展量
。最后对ΔNi求和得到总寿命：
相关文章
- 详细阅读
-
结构损伤多尺度模拟-跨尺度演化规律详细阅读
目前对在疲劳损伤过程中微裂纹成核与扩展问题的研究，大都是在单一尺度下进行。疲劳损伤累积过程中的微裂纹成核与扩展阶段的疲劳损伤过程是一个跨尺度演化行为，在细观尺度下，表现为微裂纹的成核与扩展造成的微观缺陷的增长，在宏观尺度下，表现为微裂纹扩展的群体效应造成宏观疲劳损伤累积和寿命消耗。......
2025-09-30
-
结构损伤多尺度模拟与分析：混凝土损伤特征与演详细阅读
构件受力后，钢筋和混凝土之间有相对滑移趋势时，产生摩阻力。这个过程就是钢筋混凝土粘结界面的损伤演化过程。现行钢混结构设计理论大多是基于平截面假定进行的，这隐含着钢筋和混凝土这两种性质截然不同的材料粘结良好，以确保二者变形协调。保障钢筋和混凝土的粘结良好是确保钢混结构安全的重要条件之一。图2.44钢筋与混凝土粘结失效引发的结构破坏......
2025-09-30
- 详细阅读
-
桁架结构多尺度损伤观测方法详细阅读
图2.24桁架局部损伤程度示意图实验中采用扫频试验、电测与光测相结合的方法同步采集结构动力响应与局部损伤过程的信息，实时观测裂纹尖端应变集中、热点应力分布和裂纹萌生与扩展情况，以及结构动力响应参数的变化规律。图2.25桁架结构局部与整体测区位置图2.26局部损伤区测试方案采用上述实验方案在加载的实时同步观测与分析了桁架结构的响应及其焊缝损伤区域的疲劳损伤演化过程。......
2025-09-30
-
疲劳裂纹出现过程中的损伤多尺度分析详细阅读
根据前述疲劳裂纹的萌生与演化机制的分析，演化过程可分为斜腹杆内部疲劳微裂纹萌生、扩展至表面可见裂纹与表面裂纹扩展这样三个阶段。由此可见，尽管损伤从材料层次到构件层次的演化并非跨尺度过程，其材料层次特征响应演化规律的变化也预示着构件层次特征响应的演变，材料层次损伤演化即疲劳微裂纹加速扩展的阶段同样可视为构件损伤跨层次演化的特征。......
2025-09-30
-
细观孔洞演化过程的分形维数-结构损伤多尺度模详细阅读
对于随机分布的孔洞的损伤量化问题，同样可使用分形概念进行描述，只不过这里的分形维数所表达的意义与2.2.2节中裂纹扩展的分形量化方法有所不同。图2.21ε＝59.1×10－3时孔洞体积－数量分形维数计算图2.21的计算结果表明，不同尺度细观孔洞体积与数量的分布关系可以以直线进行拟合，表明焊接细节处细观孔洞体积与数量之间具有统计意义上的分形特征。图2.22孔洞缺陷体积－数量分形维数随塑性变形的变化趋势......
2025-09-30
-
焊接区域中分形损伤的多尺度模拟与分析详细阅读
对于含多个细观孔洞的焊接损伤区域，细观孔洞体积变化趋势与反映构件宏观损伤的变化趋势一致，而且构件损伤演化很大程度上取决于细观孔洞体积演化过程。......
2025-09-30
相关推荐