金属表面总是存在着氧化物,而金属氧化物本身的表面张力比金属的表面张力要低得多。如Fe2O3、CuO、Al2O3的表面张力分别为σSV=0.35N/m、0.76N/m、0.56N/m。例如,含铝、钛沉淀强化的高温合金,虽然铝、钛含量较少,但加热时的表面氧化膜几乎都是Al2O3;含镁的铝合金尽管镁含量很少,在表面膜中也明显出现MgAlO3相。不同的氧化膜对钎料的润湿性的影响不同。......
2025-09-29
1.单个微裂纹的影响
首先分析图3.9的子问题2的余能,来推导S*的表达式。含裂纹材料的形变余能为与路径无关的M保守积分:

即含裂纹介质的余能等于准静态裂纹半径从0到a的自相似扩展过程中的能量累积。这里M定义为

将(3-38)代入(3-37),得

这里J积分等于能量释放率G

或者写成求和形式:
![]()
这里
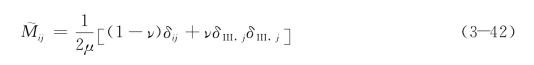
由此,式(3-39)可以转化为由应力强度因子K计算得到:

现在考虑一个含任意方向裂纹的体元,推演由于裂纹的作用导致体元力学性能的改变。如图3.11所示含一个裂纹的体元,裂纹面的方向为m。图中还显示了局部坐标的定义方式。在后面的推演中,所有符号后面加“′”标记的均为在此局部坐标系中张量或向量,整体坐标中的变量则无此标记。
已知在各向同性弹性材料中钱币状裂纹的三种类型的应力强度因子为:

对式(3-44)中的应力分量求导,可得:

图3.11 含裂纹的体元及其局部坐标系
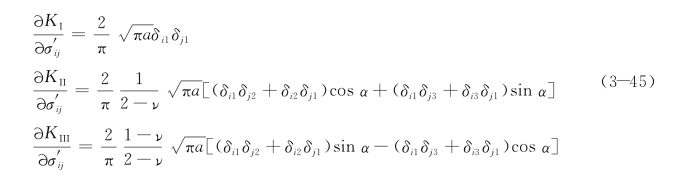
余能对应力求导可以得到柔度张量:
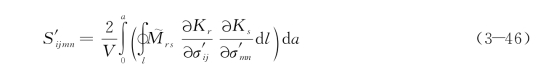
由于
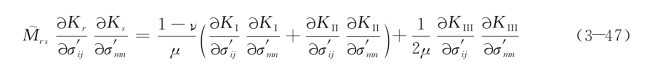
最终得到材料中存在裂纹时的柔度表达式如下:
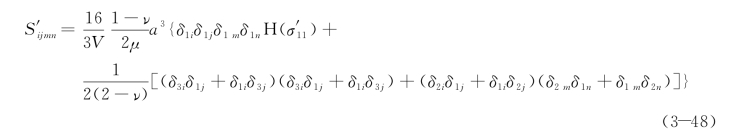
由于方向1′垂直于裂纹平面,定义向量m,使得在局部坐标系表示为:
![]()
此时式(3-48)可以重新写成:

写成更简单的形式为:
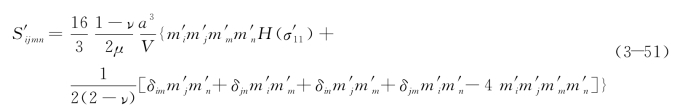
为简化上式的表达形式,定义几个四阶张量如下:

这里n为1方向的单位向量。式(3-51)于是可以写成:

此处符号![]() 表示是在局部坐标系下的表达。如果是裂纹处于张开期,则
表示是在局部坐标系下的表达。如果是裂纹处于张开期,则![]() ,此时式(3-53)可简化成:
,此时式(3-53)可简化成:
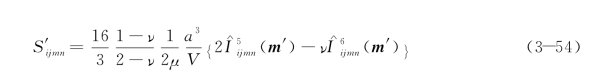 (https://www.chuimin.cn)
(https://www.chuimin.cn)
整体坐标系下的柔度可以通过坐标转换得到:
![]()
因此得到整体坐标系下的柔度为:
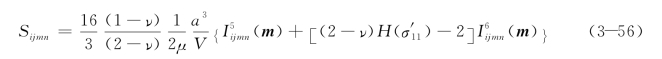
单位向量m为:
![]()
如果裂纹表面法向为拉应力![]() ,式(3-56)可以简化为:
,式(3-56)可以简化为:
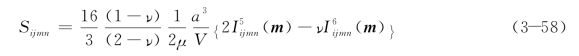
式(3-58)中的![]() 与单位向量m有关,它们可用矩阵表示为:
与单位向量m有关,它们可用矩阵表示为:
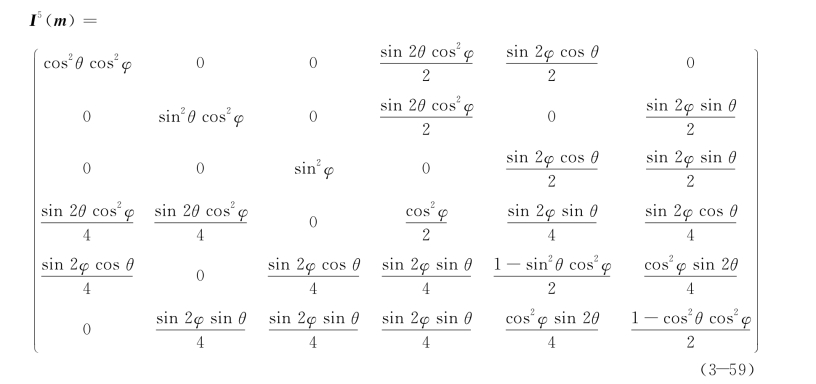
和
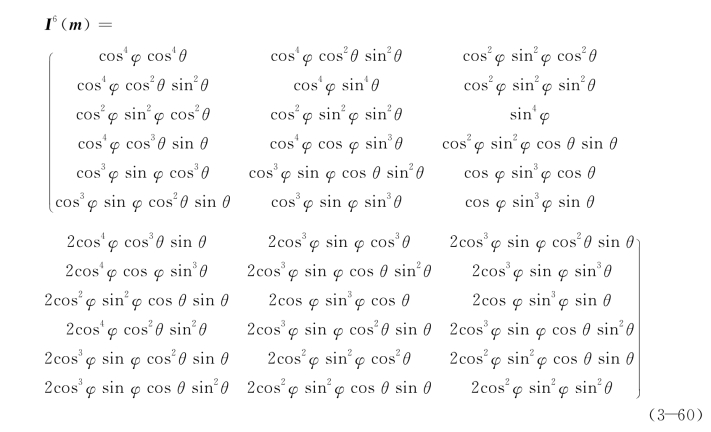
上述公式的推导参考了文献[15]中的相关思路,对此推导过程有兴趣的读者可参阅该文献。
2.大量分布微裂纹的影响
定义单位体积内裂纹密度函数w(a,θ,φ),则在(a,a+da)半径范围内,在[(φ,φ+dφ),(θ,θ+dθ)]方位范围内的单位体积裂纹数为![]() 。区域内总的裂纹数为:
。区域内总的裂纹数为:
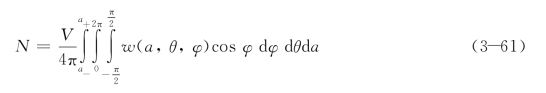
如裂纹方向与半径互不关联,则有w(a,θ,φ)=ϑ(a)ρ(θ,φ),此时有 ,
,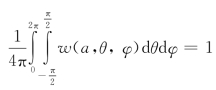 。由此,式(3-36)可以写成:
。由此,式(3-36)可以写成:
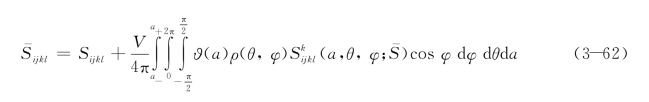
根据式(3-58),将其中的m转换成θ与φ的形式:
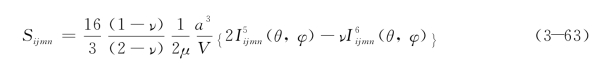
因此,式(3-62)可以写成:
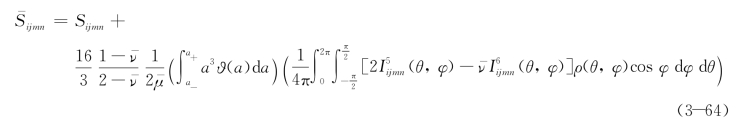
![]() 见式(3-59)和式(3-60)。定义裂纹密度的三阶矩:
见式(3-59)和式(3-60)。定义裂纹密度的三阶矩:

由于ϑ(a)的量纲为[长度]-4,因此ω为无量纲量。考虑到混凝土材料中的微裂纹方位是随机的,可取ρ(θ,φ)=1,式(3-64)化简为:
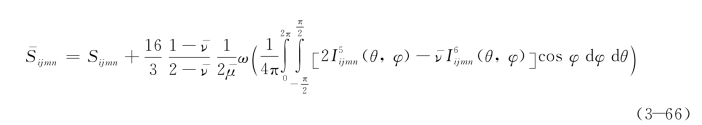
通过积分可以得到:
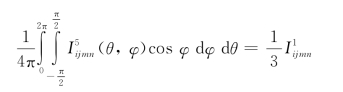
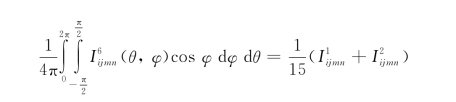
代入得到:
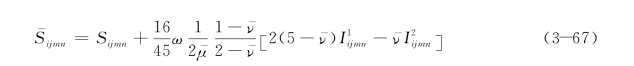
由于裂纹方位是随机的,含大量分布微裂纹材料在宏观上也呈现为各向同性。因而![]() 可表示成:
可表示成:
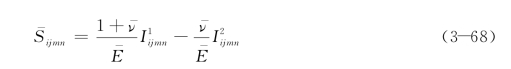
无损材料的柔度为

上式代入式(3-67),再根据![]() 的线性无关性可得到:
的线性无关性可得到:

求解得到:
相关文章

金属表面总是存在着氧化物,而金属氧化物本身的表面张力比金属的表面张力要低得多。如Fe2O3、CuO、Al2O3的表面张力分别为σSV=0.35N/m、0.76N/m、0.56N/m。例如,含铝、钛沉淀强化的高温合金,虽然铝、钛含量较少,但加热时的表面氧化膜几乎都是Al2O3;含镁的铝合金尽管镁含量很少,在表面膜中也明显出现MgAlO3相。不同的氧化膜对钎料的润湿性的影响不同。......
2025-09-29

对于船舶的阴极保护,要求牺牲阳极每单位质量的电容量和每单位体积的电容量尽可能大,这样可以减少所安装的阳极的体积。在某些情况下,例如锌牺牲阳极在温度较高的海水中,会发生晶间腐蚀,导致阳极材料性能下降。......
2025-09-29

工件表层同时渗入氮和碳,并以渗氮为主的化学热处理工艺称为氮碳共渗。根据渗剂不同,可以分为固体氮碳共渗、液体氮碳共渗、气体氮碳共渗。氮碳共渗温度 氮碳共渗温度一般为570℃。对于高速钢刀具,氮碳共渗时间一般不要超出1.5h,目的是减少脆性。渗后冷却 氮碳共渗后工件一般应快冷。图2-41 氨气分解率与白亮层厚度的关系注:渗剂为氨+酒精,氮碳共渗工艺为570℃×3h。表2-26 常用材料气体氮碳共渗后渗层深度和表面硬度(续)......
2025-09-29

本小节进一步评估了不同网络规模下DAON网络的性能,因此分别建立了包含8个、32个和64个OFBS-ONU的3个仿真场景,对应的OFBS-WSS数量分别是2、4和8,对应的OFBS-AGR数量均为2。因此,时敏业务的QoS可以得到有效保障且避免了网络规模对其产生的不利影响。图4-13不同网络规模下CN与DAON的上行平均时延图4-14不同网络规模下CN与DAON的下行平均时延图4-15和图4-16对比了分别具有8个、32个和16个OFBS-ONU的DAON网络的标准化最大吞吐量与丢包率。......
2025-09-29

混凝土的运输系统有:两条真空溜槽、两台缆机、TB1、TB2及高速供料线。高程236.00m 以下混凝土入仓方式调整为以自卸汽车为主、供料线为辅;高程236.00~280.00m 之间左岸6~9号坝段采用自卸汽车为主、供料线为辅,10~18号坝段采用供料线,19~21号坝段采用溜槽、自卸汽车与供料线结合的入仓方式;高程280.00m 以上全部采用供料线入仓。6~9号坝段仓面最大面积在高程290.00m 以上为7000m2,混凝土入仓强度为250m3/h,3号供料线加自卸汽车入仓可以满足入仓强度要求。......
2025-09-29

由于材料微观结构会影响微裂纹的扩展,即晶界严重阻碍微裂纹的扩展,绝大多数微裂纹尖端扩展到晶界处即停止。研究金属材料疲劳微裂纹扩展行为时发现,微裂纹在低应力水平下大都在0.1mm左右的长度就停止扩展,据此晶粒尺寸d0可取为0.1mm。......
2025-09-30

工艺性能是指材料适应加工工艺要求的能力。在设计零件和选择工艺方法时,都要考虑材料的工艺性能,以降低成本,获得质量优良的零件。对于金属材料而言,评价铸造性好坏的主要指标有金属液体的流动性、收缩率、偏析倾向等。材料的工艺性能往往也会影响到材料的选择,故在选材时要综合考虑。......
2025-09-29

添加剂对树脂性能的影响是多方面的,对性能的改善幅度往往很大,甚至能彻底改变原树脂的性能。常规粒度添加剂都会使复合材料的强度下降。(三)添加剂对阻燃性的影响大部分无机添加剂都会提高复合材料的阻燃性能,而有机添加剂只有少部分阻燃剂具有阻燃功能,大部分不但没有反而会助燃。(四)添加剂对导电性的影响能显......
2025-09-29
相关推荐