首页理论教育结构损伤多尺度模拟：含裂纹的脆性固体模型

结构损伤多尺度模拟：含裂纹的脆性固体模型

2023-08-26 理论教育版权反馈

【摘要】：为了简化起见，假设混凝土中的微裂纹是三维钱币状的。在建立内含大量分布微观裂纹固体的细观力学模型以前，需要首先讨论孤立裂纹的情况，然后再拓展到含大量分布微裂纹的无限大固体。

为了简化起见，假设混凝土中的微裂纹是三维钱币状的。在建立内含大量分布微观裂纹固体的细观力学模型以前，需要首先讨论孤立裂纹的情况，然后再拓展到含大量分布微裂纹的无限大固体。

1.含孤立微裂纹的无限大固体

无限大平面内的存在单个裂纹时的应力、应变场σij（x），εij（x），（x＝（x，y，z））可以分解为如图3.9所示的子问题1和子问题2的叠加，即

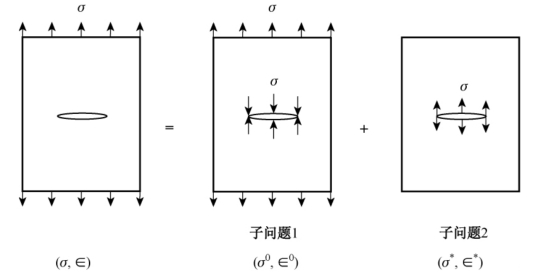
显然，对于图3.9中的子问题2，因为应力自平衡因而σ＊满足〈σ＊（x）〉＝0，此处的符号〈·〉或 pagenumber_ebook=67,pagenumber_book=57 定义为

pagenumber_ebook=67,pagenumber_book=57

图3.9　含单个裂纹的无限大固体受力状态分解

pagenumber_ebook=67,pagenumber_book=57

因此：

问题1为均匀应力场，有

定义问题2的平均应变为，同时定义映射，于是

这里为等效柔度。

2.含大量分布微裂纹的无限大固体

对于分布裂纹的问题可以参照图3.9将问题分解为如图3.10所示。类似于单个裂纹的问题，这里的应力场有，因而平均（等效）应力为：

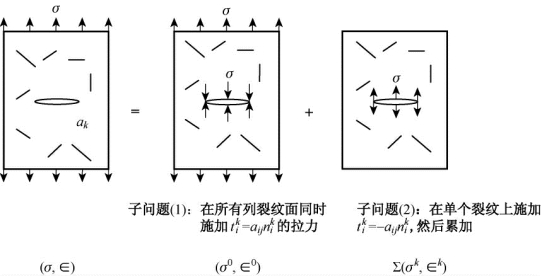
pagenumber_ebook=68,pagenumber_book=58

图3.10　含多个裂纹的无限大固体受力状态分解

而平均（等效）应变为：

pagenumber_ebook=68,pagenumber_book=58

定义 pagenumber_ebook=68,pagenumber_book=58 ，有

pagenumber_ebook=68,pagenumber_book=58

显然，如果定义映射，可以得到

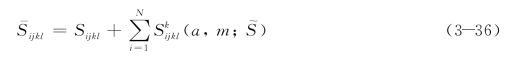
pagenumber_ebook=68,pagenumber_book=58

因而等效刚度为：

pagenumber_ebook=68,pagenumber_book=58

这里与第k个裂纹的长度及其方向向量m有关，也与基体材料参数有关。而基体材料参数的选取与所采用的细观力学分析方法有关系，如果假设裂纹是存在于原始材料中，即采用的细观力学中的Taylor模型，则选取；如果采取细观力学中的自洽（self consistent）模型，即认为裂纹是存在于性质变化后的材料中，就选取。