对于含多个细观孔洞的焊接损伤区域，细观孔洞体积变化趋势与反映构件宏观损伤的变化趋势一致，而且构件损伤演化很大程度上取决于细观孔洞体积演化过程。......
2023-08-26
焊接区域细观裂纹损伤的多尺度表征
【摘要】：同时裂纹的分布及扩展特性对损伤的影响亦不容忽视。
在含有分布细观裂纹的损伤区域，损伤程度主要取决于裂纹的数量及长度；一般裂纹长度越长，数量越多，则损伤就越严重。同时裂纹的分布及扩展特性对损伤的影响亦不容忽视。但是，由于细观裂纹萌生及扩展的不规则和随机性，现有的损伤理论不能很好地描述这种细观裂纹导致的损伤演化过程。
1.焊接裂纹型分形损伤变量定义
此前在2.2节的论述已经证明，焊接区域中的裂纹扩展形态具有很好的分形特征，而分形维数可以将裂纹导致的损伤“集中程度”量化。此外，焊接构件损伤区域的损伤程度大小还和受损区域的面积有关，对于确定的裂纹长度和分形维数而言，受损区域分布面积越大，则意味着单位面积的损伤程度越小，反之，则损伤值越大。综上所述，对于确定的具有分形特征的细观裂纹损伤区域，可定义如下损伤度量：
式中，d为裂纹分布分形维数，A为损伤区域面积，∑l为区域内所有分布裂纹总长度，随着载荷的增加，∑l会逐渐增加，表征裂纹“集中程度”的分形维数d也不断发生变化；此分形损伤度量的定义在细观裂纹几何形态的基础上，综合考虑了所有细观裂纹总长度以及裂纹扩展过程所表现出的整体分形特征，是焊接构件损伤区域内所有细观裂纹表现出的整体损伤特性。
损伤唯象理论中认为在初始无损状态时，损伤变量为0，完全损伤时，损伤变量为1；借鉴此概念，对式（3－1）所表达的损伤度量进行归一化处理，其归一化表达式如下：
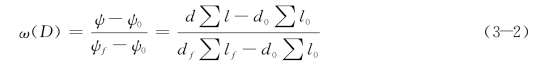
式中，ψ0为初始状态时的损伤度量，ψf为构件断裂时的损伤度量，ψ为损伤演化过程中的损伤度量，ω（D）为归一化后的损伤表征量，ω（D）的变化范围为：0＜ω（D）＜1。
式（3－2）表明，初始状态时：ψ＝ψ0，ω（D）＝0；因此，初始状态时多尺度损伤表征量ω（D）的值为0，随着塑性变形的增加，构件内部细观裂纹长度与其分布特征不断演化，因此，ψ的值逐渐趋于构件最终断裂时的值ψf，ω（D）的值也从0逐渐增加，随着细观裂纹的扩展，当ψ的值达到ψf时，构件断裂，此时ω（D）＝1。材料变形过程中，随着裂纹萌生与扩展：ψ0＜ψ＜ψf，0＜ω（D）＜1。
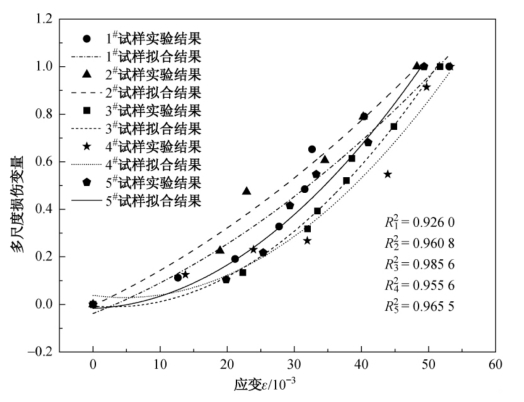
图3.1 多尺度损伤变量与塑性变形的关系
结合实验过程中的应力应变数据和裂纹扩展图像，用式（3－2）对焊接试样加载过程的裂纹扩展几何形态的变化过程进行计算，结果表明损伤表征量ω（D）随塑性变形ε的增加呈线性增加趋势，如图3.1所示。结合试验现象分析该图可知，在损伤演化初期，ω（D）较小，此时材料损伤主要表现为细观裂纹的随机扩展及萌生；随着材料损伤演化，细观裂纹逐渐扩展和贯通，局部区域开始出现集中细观裂纹，并最终发展为宏观可见裂纹，此时远离宏观裂纹的区域细观裂纹扩展缓慢或停止，损伤演化以宏观裂纹扩展和贯通为主，裂纹扩展形态仍具分形特征，ω（D）此刻同时描述了宏观和细观裂纹扩展过程。综上所述，ω（D）在整个破坏过程中既描述了裂纹从细观发展到宏观的演化过程，又反映了损伤区域的所有裂纹所表现出来的整体特性，是一个多尺度损伤表征量。
2.多尺度损伤表征方法的验证
目前损伤力学理论主要分为宏观损伤力学和细观损伤力学两个分支，其中损伤宏观唯象理论中的连续损伤变量主要是以有效承载面积来定义，但是从细观上对每一种缺陷形式和损伤机制进行分析以确定有效承载面积是很困难的，为了能间接地测定损伤，Lemaitre提出了应变等效假设。因为受损后材料的弹性模量下降，可以通过测量卸载弹性模量来标定损伤变量，根据应变等效原理，可以得到：
式中，
为受损后的弹性模量。
对于由微细观裂纹扩展导致的损伤描述，Murakami和Ohno发展了一种三维各向异性损伤理论。他们认为损伤是由微细观裂纹的群体效应造成的，损伤变量可以用一个二阶对称张量来表示：
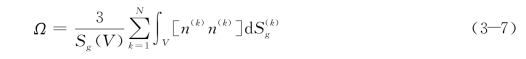
式中，
和n（k）表示第k个裂纹的长度及其单位法向量，Sg（V）为断裂时裂纹总长度。
以上两种损伤变量的定义分别描述了宏观与细观尺度下的损伤程度，仅适用于在其定义的单一尺度下的损伤问题。但焊接构件损伤演化导致破坏的过程是一个从细观到宏观的多尺度损伤演化过程，单纯用单一尺度的损伤变量难以描述损伤跨尺度演化导致破坏的完整过程。因此，需要所提出的多尺度损伤表征综合考虑裂纹从微细观到宏观扩展过程。
为了验证所提出的多尺度损伤表征方法，这里基于裂纹扩展过程中的细观裂纹量化结果以及与之同步发生的试样变形过程中有效模量的变化，分别用式（3－6）给出的宏观损伤变量和式（3－7）描述的细观损伤变量分别进行计算，并对计算结果做规格化处理，其中，设初始状态时损伤变量为0，试样断裂时损伤为1。将如上分别计算得到的结果与式（3－2）给出的多尺度损伤表征结果进行对比，对比验证的结果如图3.2所示。
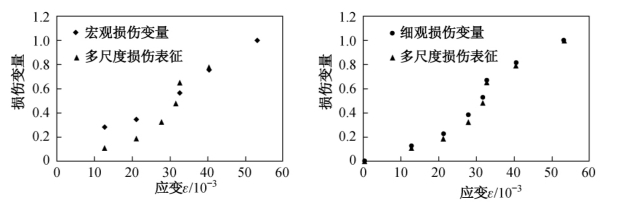
图3.2 多尺度损伤表征方法的验证
上述验证结果表明，焊接构件损伤区的微裂纹扩展过程中的多尺度损伤表征不仅物理意义明确，而且在宏观和细观两个尺度下都能够与现有的损伤表征方法可以较好地吻合。
以上的研究结果表明：基于焊接构件损伤区的分形损伤特性提出的全新的多尺度损伤表征方法具有跨尺度的物理意义；分别用现有的宏观损伤和细观损伤表征方法对其验证，结果表明新的多尺度损伤表征方法与现有的单一细观和单一宏观尺度下的损伤表征方法各自吻合较好，但所表达的物理意义比传统的损伤表征方法更为明确。这表明新的多尺度损伤表征方法能够很好地描述焊接构件中的损伤从细观裂纹萌生、扩展、聚合，发展到宏观损伤导致失效的多尺度演化过程。
有关结构损伤多尺度模拟与分析的文章
- 详细阅读
-
结构损伤多尺度模拟：细观损伤演化对连接抗震性详细阅读
从图4.22和图4.23可以看出，损伤演化的速度随着构件截面的减小而加速。图4.22加载过程中梁腹板上的损伤演化过程图4.23加载过程中梁翼缘上的损伤演化过程3.易损区域损伤演化对框架节点地震响应的影响基于上述关于易损局部损伤分布的分析，进一步研究分布损伤的演化过程对构件地震行为和承载能力的影响，其中对动态应力和抗震性能的影响是通过考虑局部损伤演化计算的结果与忽略损伤演化的计算结果之间的比较来考察。......
2023-08-26
-
混凝土材料细观损伤演化过程模拟的基本方程在结详细阅读
在基于材料细观构造图像建立了混凝土细观模型以后，还需要确定计算混凝土材料细观损伤演化过程的基本方程，包括由混凝土各细观组分材料性能决定的材料刚度矩阵计算、各细观组分材料的损伤演化率等。对于大尺寸的混凝土土木工程结构，则必须发展损伤跨尺度演化过程的自适应模拟与分析方法。......
2023-08-26
-
结构损伤多尺度模拟：含裂纹的脆性固体模型详细阅读
为了简化起见，假设混凝土中的微裂纹是三维钱币状的。在建立内含大量分布微观裂纹固体的细观力学模型以前，需要首先讨论孤立裂纹的情况，然后再拓展到含大量分布微裂纹的无限大固体。......
2023-08-26
-
焊接损伤区域裂纹扩展的分形特征简介详细阅读
分形维数是定量表示自相似形状和现象的基本量。由此可见，虽然裂纹分布及扩展形态表面上具有不规则性，但是可以通过分形维数来定量描述这种裂纹扩展形态的变化规律。图2.18ε＝0.297×10－3状态下的裂纹形态分形维数计算图2.19试样分形维数与塑性变形的关系图2.20为损伤区域细观裂纹总长度∑l 随塑性变形的变化过程，由此可见，随着塑性变形的增加，裂纹总长度呈现出线性增加的变化趋势。......
2023-08-26
-
高聚物黏结炸药的细观尺度损伤破坏模拟详细阅读
PBX 中颗粒与黏结剂之间的脱黏预测是非常重要的，因为更复杂的应力分布与脱黏破坏有关。他们认为，随着HMX 颗粒体积分数的增加，PBX 断裂阈值降低。Wang等［70］进一步发展了HMX 晶体及其黏合剂和界面的损伤模型，研究了PBX 9501 的动态力学行为和细观损伤演化机理。图1－5PBX 细观破坏模式1—界面脱黏；2—穿晶断裂；3—颗粒挤压升温......
2023-06-27
-
结构损伤多尺度模拟-结构损伤多尺度模拟与分析详细阅读
结构损伤一致多尺度分析的关键是在不同尺度的模型衔接起来进行计算，为此首先需要将前述跨尺度界面单元衔接方法引入ABAQUS，按软件指定的格式引入跨尺度界面上须满足的位移约束方程。但是由于K2本身是奇异的，同时计算机有效位数是有限的，α过大会导致系统方程病态而使计算失效。根据所建立的结构一致多尺度模型并通过宏细观变量的跨尺度关联，便可实现结构损伤的并发多尺度计算。......
2023-08-26
-
结构损伤多尺度模拟：裂纹扩展准则3.4.2详细阅读
图3.15疲劳裂纹扩展速率分区图3.15中I区的特性是存在一个“疲劳门槛”，即循环应力强度因子幅值ΔKth，在该区内应力强度因子幅值低于门槛值，疲劳裂纹基本不扩展。在高速率区，疲劳裂纹k扩展速率较快，出于简化计算和突出对II区的研究，认为裂纹扩展速率恒为，进入高速率区的判断准则为该裂纹的应力强度因子幅值ΔKth，J＞0.8 KC，J。......
2023-08-26
相关推荐