焊接损伤区域裂纹扩展的分形特征简介

2023-08-26 理论教育版权反馈

【摘要】：分形维数是定量表示自相似形状和现象的基本量。由此可见，虽然裂纹分布及扩展形态表面上具有不规则性，但是可以通过分形维数来定量描述这种裂纹扩展形态的变化规律。图2.18ε＝0.297×10－3状态下的裂纹形态分形维数计算图2.19试样分形维数与塑性变形的关系图2.20为损伤区域细观裂纹总长度∑l 随塑性变形的变化过程，由此可见，随着塑性变形的增加，裂纹总长度呈现出线性增加的变化趋势。

分形维数是定量表示自相似形状和现象的基本量。分形维数定义中的盒维数法又称覆盖法，由于易于程序化计算，应用最为广泛。

盒维数法的定义为：用正方形格子（δ×δ）去覆盖分形图形，对于给定的尺码δ，可以算出盒子数目N（δ），随着格子尺寸大小δ的变化，有一系列对应的N（δ），则盒维数计算公式为：

pagenumber_ebook=31,pagenumber_book=21

求解盒维数的具体步骤为：

（1）用边长为δ的正方形对试验照片或模拟图形进行网络化分割，计算出其中包含有裂纹的格子数目N（δ）；

（2）改变δ值，重复（1）的过程，可以得到多组δ和N（δ），对δ和N（δ）进行分析，判断其是否满足N（δ）∝δ－D，如果满足，则说明裂纹分布具有分形特征，d即为其分形维数。

编制分形维数的计算的MATLAB程序，对裂纹的二值化图像进行分形维数计算。用分形维数的网格法计算出所需的数据点，再用最小二乘法拟合分形维数值。以图2.12（a）中ε＝0.297×10－3状态下的细观裂纹图像为例，用编制的程序对其进行分形维数计算，计算结果如图2.18所示。结果表明，细观裂纹扩展过程中的分布形式满足分形规律。

用同样方法对所有试样裂纹扩展过程的全部图像分别进行分形维数计算，获得的分形维数随塑性变形的变化趋势如图2.19所示。计算结果表明所有拟合直线的线性相关系数R2均大于0.998，这说明计算得到的分形维数具有足够的可信度，也表明试样变形过程中记录的细观裂纹扩展形态确实是具有显著的分形特征，能够用分形维数去度量。

由图2.19可以看出，随着构件中塑性变形的增加，焊缝区裂纹扩展过程的分形维数呈线性增加趋势。构件中的初始裂纹分布是随机的，且随着塑性变形的增加裂纹演化模式主要表现为扩展和贯通，由于损伤在细观尺度上的不均匀性，裂纹演化的结果将会出现一个或几个裂纹分布相对密集的区域，“相对密集”的裂纹分布造成其分形维数增加，同时更有利于裂纹密集区域的损伤演化，从而使分形维数进一步增加。由此可见，虽然裂纹分布及扩展形态表面上具有不规则性，但是可以通过分形维数来定量描述这种裂纹扩展形态的变化规律。

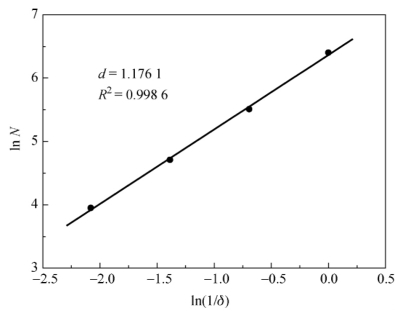
pagenumber_ebook=32,pagenumber_book=22

图2.18　ε＝0.297×10－3状态下的裂纹形态分形维数计算

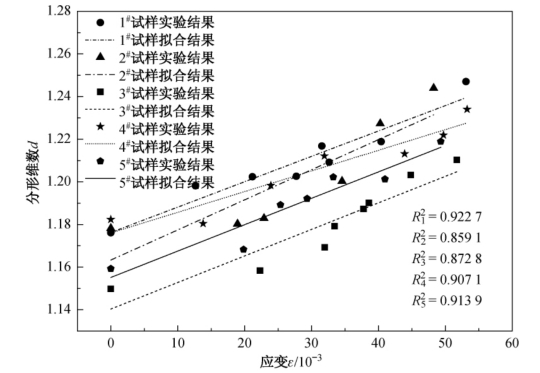
pagenumber_ebook=32,pagenumber_book=22

图2.19　试样分形维数与塑性变形的关系

图2.20为损伤区域细观裂纹总长度∑l 随塑性变形的变化过程，由此可见，随着塑性变形的增加，裂纹总长度呈现出线性增加的变化趋势。细观裂纹演化的结果造成了结构有效截面积的减小，这是造成结构宏观力学性能劣化的主要原因。虽然细观裂纹不断演化，但是构件仍保持着一定的承载能力；这是因为细观裂纹为随机分布裂纹，且每个裂纹的尺寸相对构件尺寸来讲非常小，当细观裂纹演化到一定程度，多个细观裂纹就会演化成一条主裂纹，从而导致构件有效承载面积迅速减小以致发生断裂。

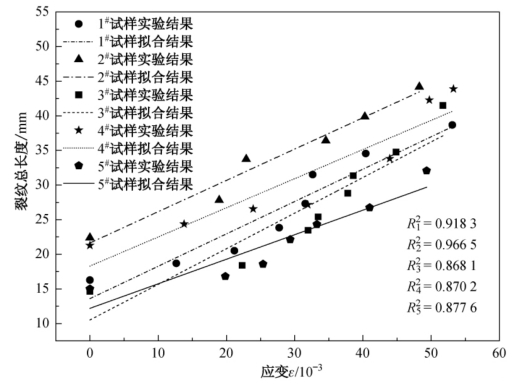
pagenumber_ebook=33,pagenumber_book=23

图2.20　细观裂纹总长度随塑性变形的变化趋势

焊接损伤区域裂纹扩展的分形特征简介

相关推荐