图9-4求内力仍采用截面法。力Q和力偶矩M就是梁弯曲时横截面上产生的两种不同形式的内力，力Q称为剪力，力偶矩M称为弯矩。简支梁受载如图9-7所示，试用截面法求截面1—1上的内力。......
2023-08-26
荷载位置固定求量值-建筑力学第3版
【摘要】：，yn，则在这组集中荷载共同作用下，量值S为应用式时，需注意竖标yi的正、负号。式表明，均布荷载引起的量值等于荷载集度乘以荷载作用段对应的影响线面积。
1.集中荷载作用
图16-8（a）所示的外伸梁上，作用一组位置确定的集中荷载P1、P2、P3。现拟求截面C的弯矩MC。为此，首先作出MC影响线，如图16-8（b）所示，并计算出对应各荷载作用点的竖标y1、y2、y3。根据叠加原理可知，在P1、P2、P3共同作用下，MC值为
一般情况下，若有一系列集中荷载P1，P2，…，Pn作用在结构上，而结构的某一量值S的影响线在各荷载作用点处的竖标为y1，y2，…，yn，则在这组集中荷载共同作用下，量值S为
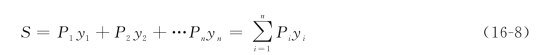
应用式（16-8）时，需注意竖标yi的正、负号。
2.分布荷载作用
如果结构在AB承受均布荷载q，如图16-9（a）所示，可将微段上的荷载qdx看作集中荷载，所引起的量值为xqdx，整个AB段均布荷载引起的量值为
式中，ω为分布荷载作用范围内影响线图形的面积。
式（16-9）表明，均布荷载引起的量值等于荷载集度乘以荷载作用段对应的影响线面积。在应用中，要注意面积ω的正负，上部面积取为正，下部取为负。
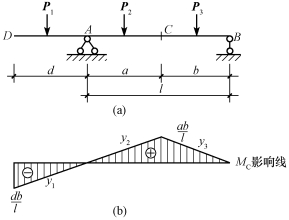
图16-8
图16-9
【例16-2】 试利用QC影响线求图16-10（a）所示简支梁C截面的剪力值。
【解】 （1）作梁的QC影响线，如图16-10（b）所示。
（2）求出力P作用点和均布荷载所对应的影响线上的纵坐标数值及面积。
（3）求简支梁C截面的剪力值。
图16-10
【例16-3】 利用影响线求图16-11（a）所示多跨静定梁的K点的弯矩MK。
【解】 先作出MK的影响线，如图16-11（b）所示。各项荷载分别计算后叠加得到：
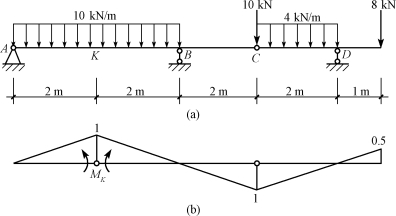
图16-11
有关建筑力学（第3版）的文章
- 详细阅读
-
建筑力学第3版：荷载分类及计算详细阅读
2）活荷载是指在施工或建成后使用期间可能作用在结构上的可变荷载。如果分布荷载在一定的范围内连续作用且其大小在各处都相同，这种荷载称为均布荷载。例如，上面所述梁的自重按每米长度均匀分布，称为线均布荷载；又如上面所述的楼面荷载，按每单位面积均匀分布，称为面均布荷载。静力荷载的特点是该荷载作用在结构上时，不会引起结构振动。......
2023-08-26
-
《建筑力学（第3版）》-叠加法求梁变形详细阅读
在小变形条件下，当梁内的应力不超过材料的比例极限时，梁的挠曲线近似微分方程是一个线性微分方程，因此可用叠加法求梁的变形，即梁在几个简单荷载共同作用下某截面的挠度和转角等于各个简单荷载单独作用时该截面挠度或转角的代数和。表9-2梁在简单荷载作用下的挠度和转角续表试用叠加法计算图9-38所示简支梁的跨中挠度yC及A截面的转角θA。......
2023-08-26
-
建筑力学（第3版）中荷载作用下位移计算的通用详细阅读
利用虚功原理推导结构在荷载作用下位移计算的一般公式，首先要确定力状态和位移状态。利用式计算结构位移时，应根据结构的具体情况，只考虑其中一项或两项。这种用虚设单位荷载产生的内力，在实际状态荷载所引起的位移上做虚功，而利用虚功原理计算结构位移的方法，称为单位荷载法。单位荷载法计算位移公式适用于弹性材料和非弹性材料，可以用于计算静定结构的位移，也可以用于计算超静定结构的位移。......
2023-08-26
-
建筑力学研究任务和内容，建筑力学第3版详细阅读
建筑力学的任务是研究结构的几何组成规律，以及在荷载作用下结构和构件的强度、刚度和稳定性问题。具体来说，建筑力学将讨论下列几个方面的内容：力系的简化和力系平衡问题。......
2023-08-26
-
建筑力学中荷载的概念及分类详细阅读
根据荷载的分布范围分类。由于这种荷载的分布面积较集中，因此，在计算简图上可将这种荷载作用于结构上的某一点处。若荷载连续作用各处大小相同，这种荷载称为均布荷载。根据荷载的作用性质分类。动力荷载的特点是该荷载作用在结构上时，会产生惯性力，从而引起结构显著的振动或冲击。......
2023-08-26
-
建筑力学（第3版）-结构的计算简图详细阅读
在选取其计算简图时，可根据实际构造和约束情况进行。在计算简图中，通常可将结点分为铰结点和刚结点两种。事实上，结构在荷载作用下，杆件之间所产生的转动也相当小，所以，该结点应视为铰结点。因而，刚结点对杆端有阻止相对转动的约束力存在，既除产生杆端轴力和剪力外，还引起杆端弯矩。计算时这种结点应视为刚结点，其计算简图如图1-23所示。......
2023-08-26
- 详细阅读
相关推荐