位移法计算连续梁及超静定刚架一般步骤如下：确定基本未知量和基本结构。用位移法计算时，只有节点转角基本未知量，故仅需建立刚节点处的力矩平衡方程，即可求解出全部未知量，进而计算杆端弯矩，绘制出内力图。此连续梁只有一个刚节点B的转角位移θB，如图15-32所示。列各杆杆端弯矩计算式。用位移法计算图15-34所示的超静定刚架，并作出弯矩图。......
2025-09-30
用力矩分配法计算连续梁与无侧移刚架（第3版）
【摘要】：对于近端，用固端弯矩叠加分配弯矩；对于远端，用固端弯矩叠加传递弯矩。用力矩分配法计算图15-40所示的连续梁，并作出M图。悬臂杆DF去掉后，节点D成为铰节点，不需进行力矩分配，简化了计算。
1.单节点力矩分配法（只有一个节点转角结构的计算）
单节点力矩分配法的计算步骤如下：
（1）确定刚节点处各杆的分配系数，并用
＝1验算。
（2）以附加刚臂固定刚节点，得到固定状态，查表15-1得到各杆端的固端弯矩MF。
（3）计算各杆近端分配弯矩。
（4）计算各杆远端传递弯矩。
（5）叠加计算出最后的各杆端弯矩。对于近端，用固端弯矩叠加分配弯矩；对于远端，用固端弯矩叠加传递弯矩。
现结合具体例子加以说明。
【例15-9】 用力矩分配法分析图15-39（a）所示的连续梁，绘制弯矩图。
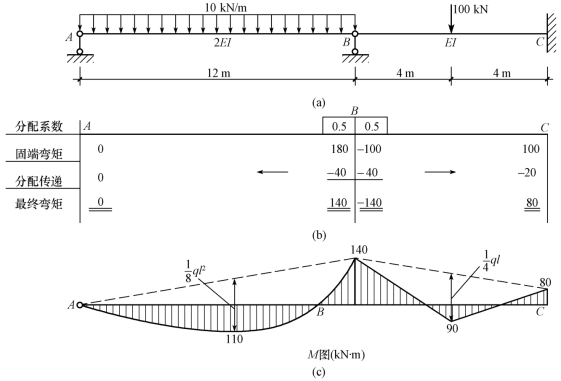
图15-39
【解】 （1）计算分配系数。两杆在节点B刚性连接，A端为链杆支座，C端为固定，两杆的转动刚度分别为
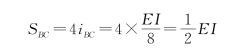
因此可得：
证明计算无误。
（2）计算固端弯矩和约束力矩。由表15-1查得各固端弯矩为
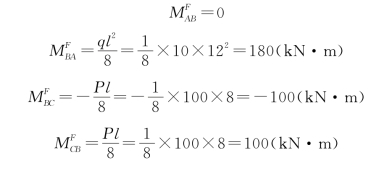
连接于节点B的各固端弯矩之和等于约束力矩MB：
（3）计算分配弯矩、传递弯矩。将分配系数乘以约束力矩的负值即得分配弯矩：
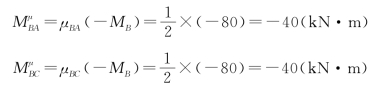
将传递系数乘以分配弯矩即得传递弯矩：
（4）计算各杆端的最终弯矩。
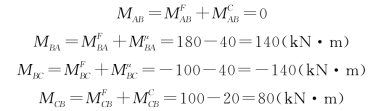
（5）画弯矩图。根据各杆端的最终弯矩和已知荷载，用叠加法画弯矩图，如图15-39（c）所示。
2.多节点力矩分配法
对于具有多个刚节点的连续梁和无侧移的刚架，只要逐次对每一个节点应用基本运算，就可计算出各杆端弯矩。下面通过具体例题说明计算步骤和格式。
【例15-10】 用力矩分配法计算图15-40所示的连续梁，并作出M图。(https://www.chuimin.cn)
【解】 （1）计算分配系数。
图15-40
（2）计算固端弯矩。DE相当于悬臂梁，截面D的弯矩作为固端弯矩作用于CD跨D端，并传递给C端作为固端弯矩。
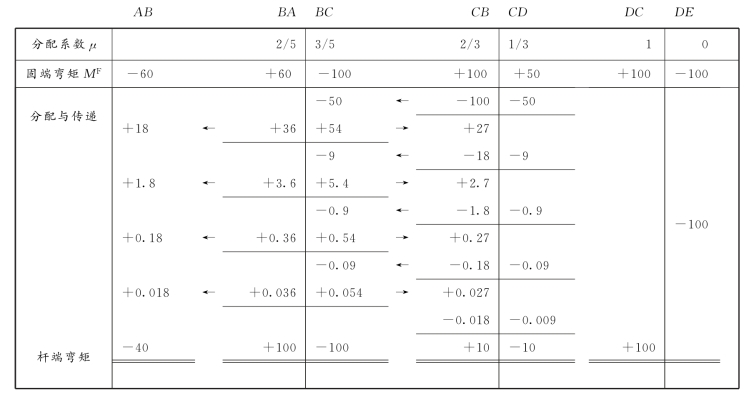
（3）列表分配传递弯矩，计算杆端弯矩，见表15-2。
表15-2 杆端弯矩计算表
（4）作弯矩图，如图15-41所示。
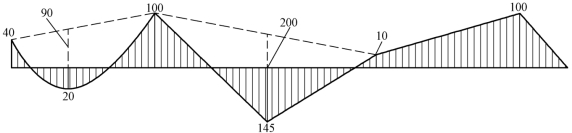
图15-41
【例15-11】 用力矩分配法计算图15-42（a）所示的刚架，绘制出弯矩图（EI为常数）。
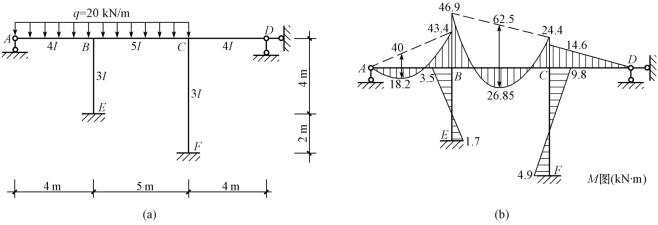
图15-42
【解】 （1）确定刚节点处各杆的分配系数，为了计算简便，令EI＝1。
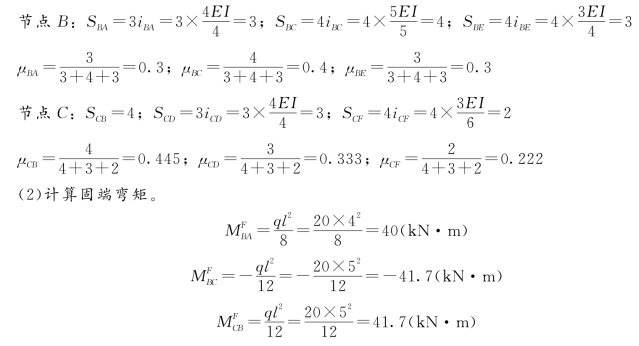
（3）分配弯矩、传递弯矩计算及最后弯矩的叠加，见表15-3。
表15-3 分配弯矩、传递弯矩计算及最后的弯矩
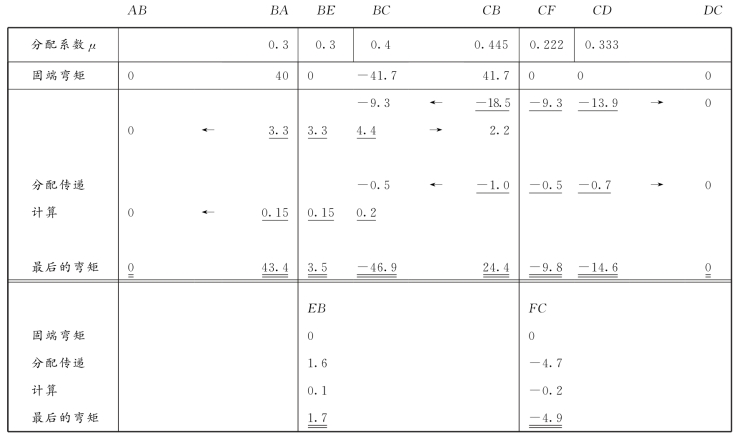
显然，刚节点B满足节点平衡条件
＝0，刚节点C满足节点平衡条件
＝0。弯矩图如图15-42（b）所示。
【例15-12】 用力矩分配法计算图15-43（a）所示的刚架，作弯矩图。
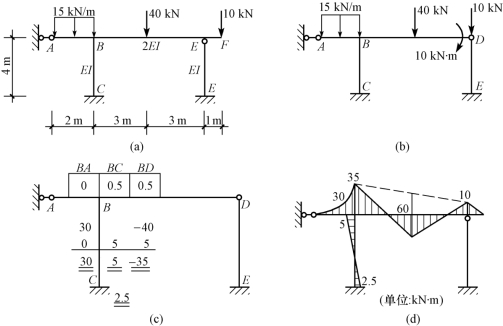
图15-43
【解】 A处虽有水平支杆，但其水平反力对AB杆的弯矩无影响，AB杆仍相当于悬臂梁。但若将悬臂杆AB去掉，并不能简化计算过程。因为在节点B处还有BC、BD两杆的刚结，仍需在节点B附加刚臂，所以AB杆不去掉。悬臂杆DF去掉后，节点D成为铰节点，不需进行力矩分配，简化了计算。原结构变成图15-43（b）所示结构进行计算。
分配系数为
固端弯矩为
力矩分配及传递如图15-43（c）所示。作原结构的弯矩图，如图15-43（d）所示。
相关文章
- 详细阅读
-
无侧移结构的位移法计算与弯矩图绘制详细阅读
只有结点角位移而无结点线位移的结构称为无侧移结构。因为只有角位移，只需建立刚结点的力矩平衡方程就可以求解出基本未知量，进而计算杆端弯矩绘制内力图。用位移法计算图15-8所示刚架，并作其弯矩图。对于具有多个结点角位移未知量的结构，可利用每个刚性结点列出一个力矩平衡方程，由于刚性结点的数目与结点角位移的数目是相同的，则所列出的位移法方程的个数与基本未知量的个数恰好相等，解联立方程即可求解出所有的基本未知量。......
2025-09-29
- 详细阅读
-
力矩分配法：建筑力学第3版直击基本概念详细阅读
图15-352.分配系数、分配弯矩图15-36所示的刚架，由于刚结点上力偶矩mA的作用而发生变形，刚结点A发生转角θA而达到平衡。杆件AB在刚结点A的分配系数μAB等于杆体AB的转动刚度与交于A点的各杆转动刚度之和的比值。同一刚结点各杆分配系数之间存在下列关系：以上的计算可简单表述为：将作用在刚结点A上的力偶矩按各杆的分配系数直接分配于各杆的A端。远端为自由端时，近端力矩、远端力矩均等于零。故将远端弯矩称为传递弯矩。......
2025-09-30
-
静定平面刚架内力计算方法(建筑力学第3版)详细阅读
静定平面刚架的内力包括弯矩、剪力与轴力。根据前述内力图绘制法逐杆绘制刚架的内力图，并进行校核。求支座反力时要根据支座的性质定出支座反力未知量的个数，然后假定反力方向，由平衡方程确定其数值。求图13-9所示刚架的支座反力。（二）刚架杆截面内力的计算1.刚架内力正负号的规定刚架的内力有弯矩、剪力和轴力。如杆端截面C1、C2的弯矩分别用MCA、MCD表示，剪力和轴力分别用QCA、QCD和NCA、NCD表示。......
2025-09-30
-
无铅钎焊用钎剂简介详细阅读
如松香在285℃将分解、碳化，失去钎剂的作用。一般希望钎剂具有不小于100℃的热稳定温度范围。活性温度范围 在活性温度范围，钎剂去除氧化物的能力最强，超出活性温度范围，钎剂将失去作用。一般来说，钎剂的活性温度范围低于钎料熔化温度10～30℃，活性温度范围上限要高于钎料的熔化温度，因此在钎焊温度下，钎剂都处于活性状态。......
2025-09-29
-
力矩分配法的基本原理简介详细阅读
现以图16-5所示只有一个刚结点的两跨连续梁为例，来说明力矩分配法的基本原理。同时在附加刚臂上产生了约束力矩，此约束力矩可以用刚结点B的力矩平衡条件求得图16-5力矩分配法基本原理即附加刚臂上的约束力矩等于刚结点B处各杆近端固端弯矩之和。用力矩分配法做题时，不必绘制图16-5、，而是按一定的格式进行计算，即可十分清晰地说明整个计算过程。......
2025-09-29
-
建筑力学第3版-悬臂梁弯矩图计算方法详细阅读
图14-15所示的在集中力及均布荷载作用下悬臂梁的弯矩图，其形状虽与图14-14相似，但不能采用其面积和形心位置公式，因为B处的剪力不为零。这时应采用图形叠加的方法解决。存在以下几种具体情况：1）如果在两个图形都是直线，则标距yC可取自其中任一图形。2）如果在两个图形中，一个是曲线，一个是直线，曲线图形只能取面积，直线图形取yC。......
2025-09-30
相关推荐