首页理论教育力矩分配法：建筑力学第3版直击基本概念

力矩分配法：建筑力学第3版直击基本概念

2023-08-26 理论教育版权反馈

【摘要】：图15-352.分配系数、分配弯矩图15-36所示的刚架，由于刚结点上力偶矩mA的作用而发生变形，刚结点A发生转角θA而达到平衡。杆件AB在刚结点A的分配系数μAB等于杆体AB的转动刚度与交于A点的各杆转动刚度之和的比值。同一刚结点各杆分配系数之间存在下列关系：以上的计算可简单表述为：将作用在刚结点A上的力偶矩按各杆的分配系数直接分配于各杆的A端。远端为自由端时，近端力矩、远端力矩均等于零。故将远端弯矩称为传递弯矩。

1.转动刚度S

转动刚度表示杆端对转动的抵抗能力，在数值上等于使杆端（或称近端）发生单位转角时需在杆端施加的力矩，用S表示。如图15-35所示，转动刚度SAB与AB杆的线刚度及远端支承有关，而与近端支承无关。

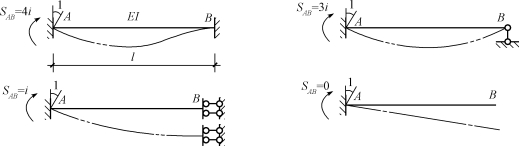
pagenumber_ebook=269,pagenumber_book=257

图15-35

2.分配系数、分配弯矩

图15-36（a）所示的刚架，由于刚结点上力偶矩mA的作用而发生变形，刚结点A发生转角θA而达到平衡。此时各杆在A端都发生了相同的转角θA，由转动刚度的定义可知：

pagenumber_ebook=269,pagenumber_book=257

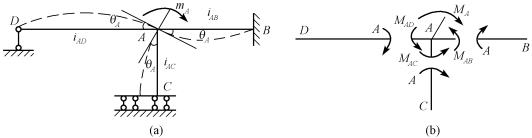
pagenumber_ebook=270,pagenumber_book=258

图15-36

取结点A为隔离体，如图15-36（b）所示，由平衡方程＝0得

整理得

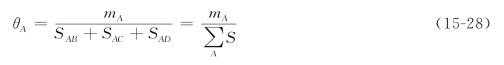
pagenumber_ebook=270,pagenumber_book=258

式中，为刚结点A所连接的各杆件转动刚度之和。

将θA值代入式（15-26）得

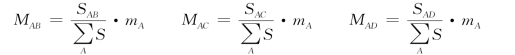
pagenumber_ebook=270,pagenumber_book=258

由此得出，各杆A端的弯矩与各杆的转动刚度成正比。可以用下列公式表示计算结果：

式中，μAi称为分配系数，μAi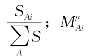＝ pagenumber_ebook=270,pagenumber_book=258 称为分配弯矩。其中i可以是B、C或D，如μAB称为杆件AB在A端的分配系数。杆件AB在刚结点A的分配系数μAB等于杆体AB的转动刚度与交于A点的各杆转动刚度之和的比值。

同一刚结点各杆分配系数之间存在下列关系：

以上的计算可简单表述为：将作用在刚结点A上的力偶矩按各杆的分配系数直接分配于各杆的A端。

3.传递系数、传递弯矩

传递系数表示近端发生转角时，杆件的远端力矩与近端力矩的比值，即

如图15-37所示，当转动端A（近端）转动某个转角θ时，A端发生近端力矩MAB，同时B端发生远端力矩MBA。以CAB表示A端转动时向B端的传递系数，以CBA表示B端转动时向A端的传递系数。

如图15-37所示，传递系数的值取决于远端的支承情况。常见杆件远端支承形式及其传递系数如下：

远端固定时[图15-37（a）]：

pagenumber_ebook=270,pagenumber_book=258

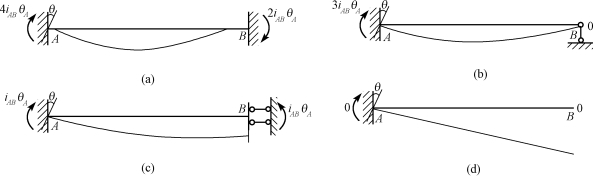
pagenumber_ebook=271,pagenumber_book=259

图15-37

远端铰支时[图15-37（b）]：

pagenumber_ebook=271,pagenumber_book=259

远端为定向支承时[图15-37（c）]：

弯矩为一常数，两端杆端弯矩正负号相反，故C为负数。

远端为自由端时，近端力矩、远端力矩均等于零。其比值传递系数可取为任意值，计算中用不到它。

根据传递系数的定义可知：远端弯矩等于近端弯矩乘以传递系数。故将远端弯矩称为传递弯矩。