位移法以结点位移作为基本未知量，结点位移包括结点角位移和结点线位移。图15-251.结点角位移的确定结点角位移比较容易确定，根据刚架的性质，同一刚结点处各杆的转角是相等的，因此，每一个刚结点只有一个独立的角位移。至于铰结点和铰支座处的角位移，结构容许自由转动，其角位移是不独立的，也不能作为基本未知量。图15-27结点角位移和结点线位移符号规定顺时针转动为正，侧移是以整个杆轴线相对于原位置顺时针转动为正。......
2023-08-26
建筑力学第3版-位移法基本结构确定
【摘要】：基本未知量确定以后，在相应的节点位移处增设相应的约束，所得的结构称为位移法基本结构。与此同时，也确定了位移法的基本未知量。由此可见，在位移法中基本未知量的数目就等于基本结构上所应具有的附加约束的数目。确定图15-29所示结构的位移法基本结构。
基本未知量确定以后，在相应的节点位移处增设相应的约束（刚节点处增加刚臂，线位移处增加相应的链杆），所得的结构称为位移法基本结构。
下面举例说明如何将原结构化为基本结构。
如图15-28（a）所示的刚架，在荷载作用下结构发生了变形，节点C、D发生了转动和移动。
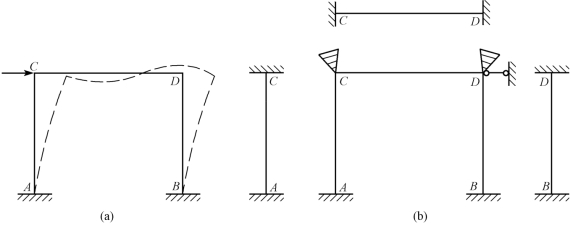
图15-28
为了阻止节点移动，向节点D（或节点C）上加一附加支杆（其作用是阻止节点线位移而不限制节点转动），如图15-28（b）所示。对于以弯矩为主要内力的受弯直杆，可略去轴向变形和剪切变形的影响，且由于弯曲变形是微小的，杆处于微弯状态。因此，假定受弯直杆两端之间的距离在变形前后保持不变，这样，节点D就不移动了。由于节点D、节点A不移动，节点C也不移动了。故该结构只需加一个附加支杆，所有节点就不能移动而只能转动了。
为了阻止节点转动，在节点C、D上各加一个刚臂（其作用是阻止节点转动而不限制节点的线位移）。此时，节点C、节点D均不能移动和转动，成为周围各杆的固定支座。于是杆AC、杆CD、杆DB均化为两端固定梁，图15-28（b）所示的梁即为图15-28（a）所示原结构的位移法基本结构。
与此同时，也确定了位移法的基本未知量。因为在选定位移法基本结构时，为了使各杆都化为单跨超静定梁应在每一个刚节点上加入附加刚臂以阻止其转动，显然，附加刚臂的数目恰好等于结构中刚节点的数目；另外，还需加入一定数量的附加支杆以阻止各节点发生线位移，附加支杆的数目显然与原结构各节点的独立线位移数目相等。由此可见，在位移法中基本未知量的数目就等于基本结构上所应具有的附加约束的数目。因此，在选定基本结构的同时，基本未知量的数目也就确定了。
顺便指出，为了得到基本结构，有些情况并不需要将所有节点都变成不动节点。因为虽然结构中某些节点也有角位移或线位移，但由于分析内力时可以不需要先计算出该位移，因而不必将它列入基本未知量内，以减少计算工作量。
【例15-5】 确定图15-29（a）所示结构的位移法基本结构。
【解】 化为铰接体系（未画出）不难看出，需加入两根附加支杆才能使其形成几何不变体系。
在刚节点B、C、D处加入三个附加刚臂。
图15-29
位移法基本结构如图15-29（b）所示。
有关建筑力学（第3版）的文章
- 详细阅读
-
建筑力学（第3版）：位移法的基本原理和解题思详细阅读
为了说明位移法的基本思路，下面用位移法分析图15-25所示的简单刚架。分析这两个单跨超静定梁，建立其杆端转角和杆端内力的函数关系。利用结构结点B的力矩平衡条件[图15-25]建立位移法方程：即由此解得θB＝，代入式，计算出各杆杆端弯矩，作弯矩图，如图15-25所示。由位移法的解题思路可见，位移法分析需要解决以下几个问题：确定结构的独立结点位移，即位移法的基本未知量。......
2023-08-26
-
结构力学：位移法概念简介详细阅读
位移法是以结构的结点位移作为基本未知量，取超静定的单个杆件及其组成的体系作为基本结构，通过平衡条件建立位移法方程，求出位移后，即可利用位移和内力之间的关系，求出杆件和结构的内力。通过下面简单例子具体说明位移法的基本原理和计算方法。综上所述，位移法的基本思路是“先固定后复原”。......
2023-08-30
-
结构力学：线位移法数目确定详细阅读
在确定结点线位移的数目时，由于不计受弯直杆的轴向变形，并且假设弯曲变形是微小的，即认为直杆在受弯前后其投影长度保持不变。由于在确定结点线位移数目时，不计及杆件的轴向变形和弯曲变形，因此，可以先把所有的刚性结点和固定支座全部改成铰接，使结构变成一个铰接体系。结构基本未知量的总数等于结点的角位移数和线位移数之和。......
2023-08-30
-
力法基本原理-建筑力学（第3版）详细阅读
力法是计算超静定结构最基本的方法，下面先用一个例子说明力法的基本原理。这个静定梁称为原超静定梁的基本结构。若用Δ1q和Δ11分别表示荷载q和多余未知力X1单独作用下基本结构在X1作用处沿X1方向产生的位移，则由叠加原理根据位移条件可得下列方程：若X1＝1，在X1方向产生的位移为δ11，则有Δ11＝δ11X1，于是式可以写成这就是求解多余未知力的补充方程，称为力法方程。......
2023-08-26
-
建筑力学：支座移动时位移计算，第3版详细阅读
图14-21所示的刚架，支座移动为C1、C2、C3，致使整个结构移动到了虚线位置。将支座反力和对应的位移代入式，计算位移。由于A支座无位移，故只需计算B支座反力即可。计算结果为正，说明ΔCV与虚设单位力的方向一致。......
2023-08-26
-
建筑力学（第3版）-结构的计算简图详细阅读
在选取其计算简图时，可根据实际构造和约束情况进行。在计算简图中，通常可将结点分为铰结点和刚结点两种。事实上，结构在荷载作用下，杆件之间所产生的转动也相当小，所以，该结点应视为铰结点。因而，刚结点对杆端有阻止相对转动的约束力存在，既除产生杆端轴力和剪力外，还引起杆端弯矩。计算时这种结点应视为刚结点，其计算简图如图1-23所示。......
2023-08-26
-
截面法求内力-建筑力学（第3版）详细阅读
图9-4求内力仍采用截面法。力Q和力偶矩M就是梁弯曲时横截面上产生的两种不同形式的内力，力Q称为剪力，力偶矩M称为弯矩。简支梁受载如图9-7所示，试用截面法求截面1—1上的内力。......
2023-08-26
相关推荐