静定平面刚架的内力包括弯矩、剪力与轴力。根据前述内力图绘制法逐杆绘制刚架的内力图，并进行校核。求支座反力时要根据支座的性质定出支座反力未知量的个数，然后假定反力方向，由平衡方程确定其数值。求图13-9所示刚架的支座反力。（二）刚架杆截面内力的计算1.刚架内力正负号的规定刚架的内力有弯矩、剪力和轴力。如杆端截面C1、C2的弯矩分别用MCA、MCD表示，剪力和轴力分别用QCA、QCD和NCA、NCD表示。......
2025-09-30
力法应用：建筑力学（第3版）计算超静定梁内力、绘制弯矩图
【摘要】：根据上述力法原理，用力法计算超静定结构内力的计算步骤如下：去掉原结构的多余约束并代之以多余未知力，选取基本体系。试用力法计算图15-12所示超静定梁的内力，并绘制出弯矩图。由基本体系在多余未知力X1及荷载的共同作用下，B点处沿X1方向上的位移等于零的变形条件，建立力法方程为计算方程中的系数和自由项。因此，它的弯矩图与同跨度、同荷载的简支梁相比较，最大弯矩峰值较小，使整个梁上内力分布得以改善。
根据上述力法原理，用力法计算超静定结构内力的计算步骤如下：
（1）去掉原结构的多余约束并代之以多余未知力，选取基本体系。
（2）根据基本结构在多余未知力和原荷载的共同作用下，在去掉多余约束处的位移应与原结构中相应的位移相同的位移条件，建立力法典型方程。
（3）作出基本结构的单位内力图和荷载内力图，或写出内力表达式，按计算静定结构位移的方法，计算系数和自由项。
（4）解力法方程，求解多余未知力。
（5）作内力图。
【例15-1】 试用力法计算图15-12（a）所示超静定梁的内力，并绘制出弯矩图。
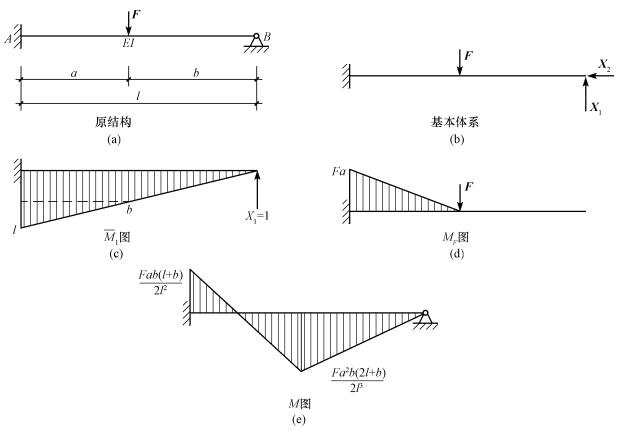
图15-12
【解】 （1）选取基本体系。此梁为二次超静定结构，现去掉B端的固定铰支座，代之以多余未知力X1、X2，得到一悬臂梁基本体系，如图15-12（b）所示。在竖向荷载作用下，当不计梁中轴向变形时，X2＝0（对于其他支承形式的单跨梁，同样可认为轴向约束力为零）。故只需计算多余未知力X1。
（2）建立力法方程。由基本体系在多余未知力X1及荷载的共同作用下，B点处沿X1方向上的位移等于零的变形条件，建立力法方程为
（3）计算方程中的系数和自由项。分别绘制出基本体系在单位多余未知力X1＝1作用下的弯矩图
，如图15-12（c）所示，以及荷载作用下的弯矩图MF，如图15-12（d）所示。由图乘法有：
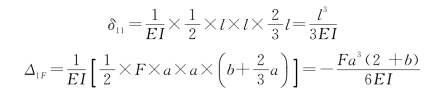
（4）解方程求多余未知力。将求得的系数和自由项代入力法方程，有：
解得
（5）绘制弯矩图。由M＝
绘制出的弯矩图如图15-12（e）所示。
由以上计算可知，由于超静定梁受多余约束限制，在固定端不能产生转角位移而使梁上侧纤维受拉。因此，它的弯矩图与同跨度、同荷载的简支梁相比较，最大弯矩峰值较小，使整个梁上内力分布得以改善。
【例15-2】 试用力法计算如图15-13（a）所示刚架的内力，并绘制内力图。
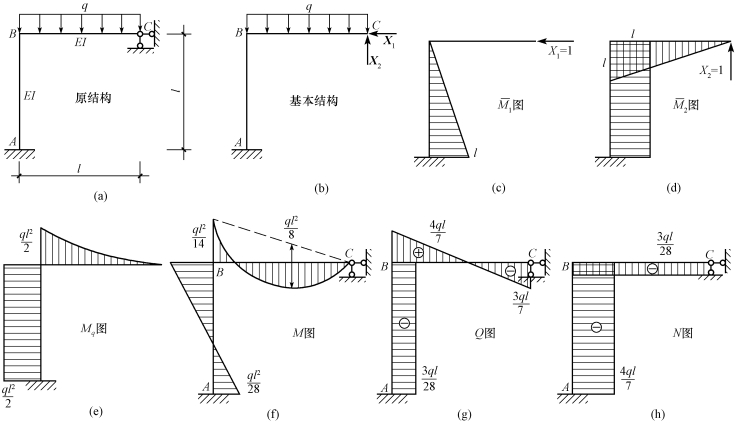
图15-13(https://www.chuimin.cn)
【解】 （1）选取基本结构。本题为二次超静定结构，去掉C处的两个多余约束，得基本结构，如图15-13（b）所示。
（2）建立力法典型方程。
（3）绘制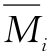
和Mq图，如图15-13（c）、（d）、（e）所示，计算系数和自由项。
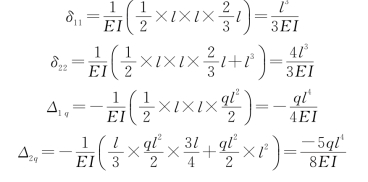
（4）求解多余未知力。
（5）根据叠加原理绘制M图，如图15-13（f）所示。
（6）根据静力平衡条件绘制Q图和N图，分别如图15-13（g）、（h）所示。
【例15-3】 计算图15-14（a）所示排架柱的内力，并作出弯矩图。
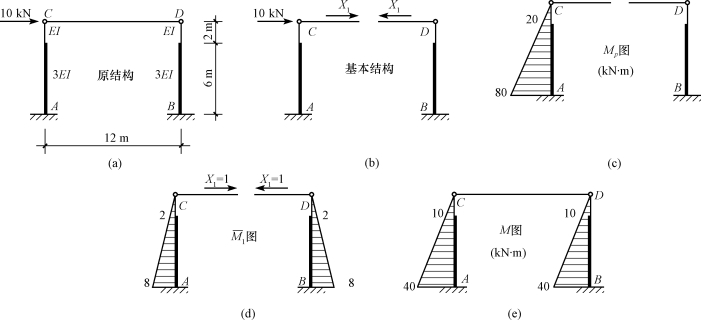
图15-14
【解】 （1）选取基本结构。此排架是一次超静定结构，切断横梁代之以多余未知力X1得到基本结构，如图15-14（b）所示。
（2）建立力法方程。
（3）计算系数和自由项。分别作基本结构的荷载弯矩图MP图和单位弯矩图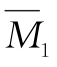
图，如图15-14（c）、（d）所示。
利用图乘法计算系数和自由项分别如下：
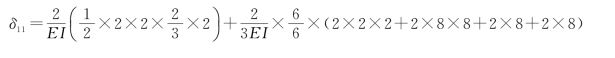
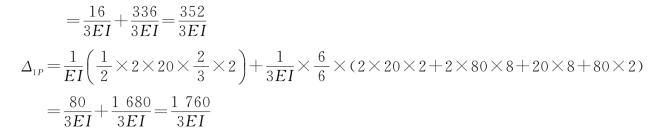
（4）计算多余未知力。将系数和自由项代入力法方程，得
解得
（5）作弯矩图。按公式M＝
即可作出排架最后的弯矩图，如图15-14（e）所示。
相关文章
- 详细阅读
-
建筑力学（第3版）-叠加法梁内力图详细阅读
在小变形条件下，梁的内力、支座反力、应力和变形等参数均与荷载呈线性关系，每一荷载单独作用时引起的某一参数不受其他荷载的影响。为了便于应用叠加法绘制内力图，表9-1中给出了梁在简单荷载作用下的弯矩图，可供查用。由上例可以看出，用分段叠加法作外伸梁的弯矩图时，不需要求支座反力，就可以画出其弯矩图。......
2025-09-30
-
截面法求内力-建筑力学（第3版）详细阅读
图9-4求内力仍采用截面法。力Q和力偶矩M就是梁弯曲时横截面上产生的两种不同形式的内力，力Q称为剪力，力偶矩M称为弯矩。简支梁受载如图9-7所示，试用截面法求截面1—1上的内力。......
2025-09-30
-
《建筑力学（第3版）》探索简易法作梁的内力图详细阅读
在集中力偶作用处，剪力图无变化；弯矩图有突变，其突变值等于该集中力偶的大小。某外伸梁如图9-15所示，已知l＝4m，试用简易法绘制此梁的剪力图和弯矩图。AB段梁上有均布荷载，该段梁的剪力图为斜直线，通过画出该斜直线。该段梁的弯矩图为二次曲线。......
2025-09-30
-
建筑力学（第3版）：轴向拉杆内力-轴力详细阅读
现分析其任一截面m—m上的内力。内力的作用线与杆轴线重合，称为轴向内力，简称轴力，用符号N表示。背离截面的轴力，称为拉力；而指向截面的轴力，称为压力。在求轴力时，通常将轴力假设为拉力方向，这样由平衡条件求出结果的正负号，就可直接代表轴力本身的正负号。根据平衡条件列平衡方程：截面2—2处的杆件轴力N2。......
2025-09-30
-
单跨静定梁内力分析方法及其应用详细阅读
单跨静定梁在实际工程中应用较多，例如一般钢筋混凝土过梁、起重机梁等，其内力分析方法已在第六章中作了详细介绍。作内力图时，轴力图、剪力图要注明正负号，弯矩图规定画在杆件受拉的一侧，不用注明正负号。由于图12-7所示两个微段荷载应为等值，故有qdx＝q′ds由此可得图12-7斜梁上荷载沿轴线方向分布单跨斜梁的内力除了弯矩和剪力之外，还有轴向力。......
2025-09-29
-
用力法求解超静定梁的方法和步骤详细阅读
计算超静定梁的位移时，通常忽略轴力和剪力的影响，只考虑弯矩的影响。因而系数及自由项按照下列公式计算：试用力法作图14-13所示单跨超静定梁的弯矩图。此梁具有三个多余约束，为三次超静定。将以上各值代入力法方程，而在前两式中消去后，得解以上方程组求得由力法方程的第三式求解X3时，可以看出，按不同的假设有不同的结果。......
2025-09-29
-
力法基本原理-建筑力学（第3版）详细阅读
力法是计算超静定结构最基本的方法，下面先用一个例子说明力法的基本原理。这个静定梁称为原超静定梁的基本结构。若用Δ1q和Δ11分别表示荷载q和多余未知力X1单独作用下基本结构在X1作用处沿X1方向产生的位移，则由叠加原理根据位移条件可得下列方程：若X1＝1，在X1方向产生的位移为δ11，则有Δ11＝δ11X1，于是式可以写成这就是求解多余未知力的补充方程，称为力法方程。......
2025-09-30
相关推荐