在第一章中，已对几何法进行了介绍，知道了两个汇交于一点的力F1和F2如何应用力的平行四边形法则和三角形法则求它们的合力R。设作用于物体上A点的力F1、F2、F3、F4组成平面汇交力系，现求其合力，如图2-2所示。这种由各分力和合力构成的多边形abcde称为力多边形。这种求合力矢的几何作图法被称为力多边形法。拉力F1、F2、F3的作用力汇交于O点，构成平面汇交力系。......
2023-08-26
力法基本原理-建筑力学（第3版）
【摘要】：力法是计算超静定结构最基本的方法，下面先用一个例子说明力法的基本原理。这个静定梁称为原超静定梁的基本结构。若用Δ1q和Δ11分别表示荷载q和多余未知力X1单独作用下基本结构在X1作用处沿X1方向产生的位移，则由叠加原理根据位移条件可得下列方程：若X1＝1，在X1方向产生的位移为δ11，则有Δ11＝δ11X1，于是式可以写成这就是求解多余未知力的补充方程，称为力法方程。
力法是计算超静定结构最基本的方法，下面先用一个例子说明力法的基本原理。
图15-9（a）所示的一次超静定梁，EI为常数。如果撤去B处支座链杆并以多余未知力X1代替，便成为图15-9（b）所示的静定梁。这个静定梁称为原超静定梁的基本结构。原超静定梁称为原结构。只要能设法求出多余未知力X1，则其余支座反力和内力的计算就与静定结构相同。
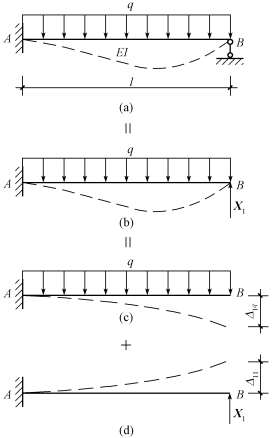
图15-9
基本结构在B端不再受约束限制，因此在荷载q作用下B点竖向位移向下[图15-9（c）]，在X1作用下B点竖向位移向上[图15-9（d）]。显然在二者共同作用下，B点竖向位移将随X1的大小不同而异，由于X1是取代了被拆去约束对原结构的作用，因此，基本结构的变形位移状态应与原结构完全一致，即B点的竖向位移Δ1必须为零，也就是说基本结构在已知荷载与多余未知力X1共同作用下，在拆除约束处沿多余未知力X1作用方向产生的位移应与原结构在X1方向的位移相等。即Δ1＝0就是基本结构应满足的变形谐调条件，又称位移条件。
若用Δ1q和Δ11分别表示荷载q和多余未知力X1单独作用下基本结构在X1作用处沿X1方向产生的位移（符号Δ1q和Δ11中第一个下标表示位移发生的地点与方向，第二个下标表示引起位移的原因），则由叠加原理根据位移条件可得下列方程：
若X1＝1，在X1方向产生的位移为δ11，则有Δ11＝δ11X1，于是式（15-1）可以写成
这就是求解多余未知力的补充方程，称为力法方程。式中δ11和Δ1q都是静定结构在已知荷载作用下产生的位移，因而可用第十四章介绍的计算位移的方法求得，将其代入式（15-2）即可解得多余未知力X1。
为了计算δ11和Δ1q，分别作基本结构在荷载q作用下的弯矩图Mq[图15-10（a）]和在单位力X1＝1作用下的单位弯矩图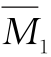
[图15-10（b）]，应用图乘法可得
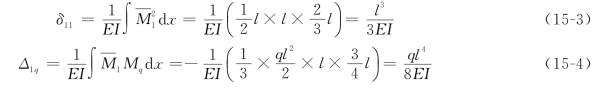
代入力法方程式（15-2）得
由此解得
X1为正，表示所设的X1方向与实际方向相同。
多余未知力X1求得后，即可由静力平衡条件求得其余的约束反力和内力。最后，弯矩图也可以利用已经绘制出的基本结构的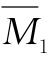
图[图15-10（c）]和Mq图由叠加原理按下式求得：
也就是将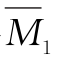
图的竖标乘以X1倍，再与Mq图中的对应竖标相加，计算出控制截面的弯矩值后，绘制出超静定结构的M图，如图15-10（d）所示。
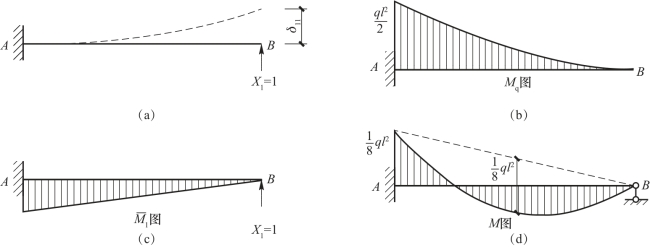
图15-10
有关建筑力学（第3版）的文章
- 详细阅读
-
建筑力学（第3版）：位移法的基本原理和解题思详细阅读
为了说明位移法的基本思路，下面用位移法分析图15-25所示的简单刚架。分析这两个单跨超静定梁，建立其杆端转角和杆端内力的函数关系。利用结构结点B的力矩平衡条件[图15-25]建立位移法方程：即由此解得θB＝，代入式，计算出各杆杆端弯矩，作弯矩图，如图15-25所示。由位移法的解题思路可见，位移法分析需要解决以下几个问题：确定结构的独立结点位移，即位移法的基本未知量。......
2023-08-26
-
结构力学,力法基本原理解析详细阅读
如图 6-8所示，X1表示被去掉的多余约束的反力，暂时是未知的，故称为多余约束未知力或力法的基本未知量。由于 δ11和 Δ1F是静定结构在已知力作用下的位移，均可按前章所述计算位移的方法求得，因此，解上述方程，可求得多余未知力X1。......
2023-08-30
-
力法应用：建筑力学（第3版）计算超静定梁内力详细阅读
根据上述力法原理，用力法计算超静定结构内力的计算步骤如下：去掉原结构的多余约束并代之以多余未知力，选取基本体系。试用力法计算图15-12所示超静定梁的内力，并绘制出弯矩图。由基本体系在多余未知力X1及荷载的共同作用下，B点处沿X1方向上的位移等于零的变形条件，建立力法方程为计算方程中的系数和自由项。因此，它的弯矩图与同跨度、同荷载的简支梁相比较，最大弯矩峰值较小，使整个梁上内力分布得以改善。......
2023-08-26
-
截面法求内力-建筑力学（第3版）详细阅读
图9-4求内力仍采用截面法。力Q和力偶矩M就是梁弯曲时横截面上产生的两种不同形式的内力，力Q称为剪力，力偶矩M称为弯矩。简支梁受载如图9-7所示，试用截面法求截面1—1上的内力。......
2023-08-26
-
《建筑力学第3版》-细长压杆临界力计算详细阅读
以上讨论的是两端铰支的细长压杆的临界力计算。对于其他支承形式的压杆，也可用同样方法导出其临界力的计算公式。因此，可将两端铰支约束压杆的挠曲线形状取为基本情况，而将其他杆端约束条件下压杆的挠曲线形状与之进行对比，从而得到相应杆端约束条件下压杆临界力的计算公式。表11-1各种支承约束条件下等截面压杆临界力的欧拉公式以上讨论的都是理想的支承情况。现分别计算两种截面杆的临界力。......
2023-08-26
-
建筑力学（第3版）：轴向拉杆内力-轴力详细阅读
现分析其任一截面m—m上的内力。内力的作用线与杆轴线重合，称为轴向内力，简称轴力，用符号N表示。背离截面的轴力，称为拉力；而指向截面的轴力，称为压力。在求轴力时，通常将轴力假设为拉力方向，这样由平衡条件求出结果的正负号，就可直接代表轴力本身的正负号。根据平衡条件列平衡方程：截面2—2处的杆件轴力N2。......
2023-08-26
-
力对点的矩及其作用-建筑力学第3版详细阅读
力对点的矩是一个代数量，其绝对值等于力的大小与力臂之积，其正负可作如下规定：力使物体绕矩心逆时针转动时取正号；反之取负号。力F对O点的矩，以符号mO表示，即O点称为转动中心，简称矩心。试求两个力对A点的力矩。图3-3二力对A点的力矩分别为计算结果表明，力F2使物体绕A点转动的效果大于力F1所产生的转动效果，板将绕A点顺时针方向转动。......
2023-08-26
相关推荐