建筑力学第3版-悬臂梁弯矩图计算方法

2023-08-26 理论教育版权反馈

【摘要】：图14-15所示的在集中力及均布荷载作用下悬臂梁的弯矩图，其形状虽与图14-14相似，但不能采用其面积和形心位置公式，因为B处的剪力不为零。这时应采用图形叠加的方法解决。存在以下几种具体情况：1）如果在两个图形都是直线，则标距yC可取自其中任一图形。2）如果在两个图形中，一个是曲线，一个是直线，曲线图形只能取面积，直线图形取yC。

（1）图中标准抛物线图形顶点位置的确定。顶点是指该点的切线平行于基线的点，即顶点处截面的剪力应等于零。图14-15所示的在集中力及均布荷载作用下悬臂梁的弯矩图，其形状虽与图14-14（c）相似，但不能采用其面积和形心位置公式，因为B处的剪力不为零。这时应采用图形叠加的方法解决。

pagenumber_ebook=234,pagenumber_book=222

图14-15

（2）若遇较复杂的图形不便确定形心位置，则应运用叠加原理，将图形分解后分别图乘，然后求其结果的代数和。存在以下几种具体情况：

1）如果在两个图形都是直线，则标距yC可取自其中任一图形。

2）如果在两个图形中，一个是曲线，一个是直线，曲线图形只能取面积，直线图形取yC。

3）如果两个都是梯形[图14-16（a）]，则可以将它分解成两个三角形，分别图乘后再叠加，即

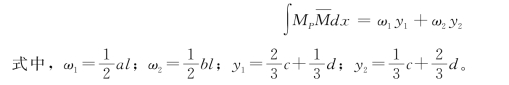
pagenumber_ebook=234,pagenumber_book=222

4）若MP图和 pagenumber_ebook=234,pagenumber_book=222 图均有正、负两部分[图14-16（b）]，则可将MP图看作是两个三角形的叠

加，三角形ABC在基线的上边为正值，高度为a；三角形ABD在基线的下边为负值，高度为b。然后，将两个三角形面积各乘以相应的图的竖标（注意乘积结果的正负）再叠加。即

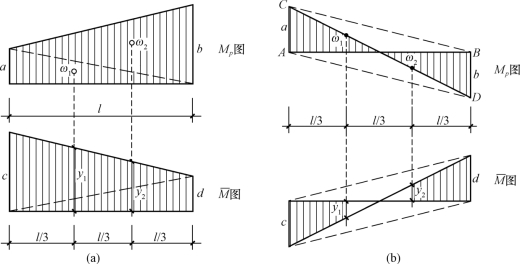
pagenumber_ebook=234,pagenumber_book=222

图14-16

5）如果一个图形是曲线，另一个图形是由几段直线组成的折线，如图14-17（a）所示，或者各杆段的EI不相等时，则应分段考虑，如图14-17（b）所示。即

6）对于图14-18所示由于均布荷载q所引起的MP图，可以将它看作是两端弯矩竖标所连成的梯形ABDC与相应简支梁在均布荷载作用下的弯矩图叠加而成，后者即虚线CD与曲线之间所围部分。将MP图分解成上述两个简单图形后，分别与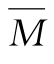 pagenumber_ebook=234,pagenumber_book=222 图作图乘运算，再相叠加，即得所求结果。

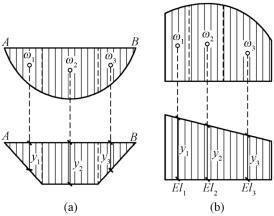
pagenumber_ebook=235,pagenumber_book=223

图14-17

pagenumber_ebook=235,pagenumber_book=223

图14-18

建筑力学第3版-悬臂梁弯矩图计算方法

相关推荐