根据力的平移定理，将各力平移到O点，其结果得到一个作用于O点的平面汇交力系，，…附加的平面力偶系可以合成一合力偶，其力偶矩MO称为原力系向O点简化的主矩。这个力作用在简化中心，它的矢量称为原力系的主矢，并等于原力系中各力的矢量和；这个力偶的力偶矩称为原力系对简化中心的主矩，并等于原力系中各力对简化中心之矩的代数和。......
2025-09-30
建筑力学第3版：弹性体系的互等定理
【摘要】：线性变形体系的功的互等定理和位移互等定理在位移计算及分析超静定结构时将会用到。代入功的互等定理式，则有：即式即弹性结构的位移互等定理表达式。
线性变形体系的功的互等定理和位移互等定理在位移计算及分析超静定结构时将会用到。
1.功的互等定理
功的互等定理是指同一弹性结构在两种不同状态下的虚功相等。如图14-4所示的简支梁，分别作用两组外力P1与P2，并分别称为第一状态[图14-4（a）]和第二状态[图14-4（b）]。计算第一状态的外力及其所引起的内力在第二状态的相应位移和变形上所做的虚功T12和W12时，据虚功原理有T12＝W12，即
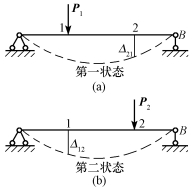
图14-4
式中 Δ12——由P2力引起的在P1力作用点沿P1力方向的位移。
反之，计算第二状态的外力及其所引起的内力在第一状态的相应位移和变形上所做的虚功T21和W21时，据虚功原理有T21＝W21，即
式中 Δ21——由P1力引起的在P2力作用点沿P2力方向的位移。
比较式（14-8）和式（14-9），有：
也可写为
式（14-11）表明，第一状态的外力在第二状态的位移上所做的虚功，等于第二状态的外力在第一状态的位移上所做的虚功。这就是功的互等定理。
功的互等定理可以推广到任何弹性结构。
2.位移互等定理
在功的互等定理中，假如两个状态中的荷载是单位力时（P1＝1，P2＝1），为了明显起见，由单位力所引起的位移，用小写字母δ12、δ21表示，如图14-5所示。代入功的互等定理式（14-10），则有：
即
式（14-12）即弹性结构的位移互等定理表达式。该定理表明：对任何弹性结构，单位力P2＝1在单位力P1作用点的截面产生的位移δ12（沿P1方向），等于单位力P1＝1在单位力P2作用点的截面产生的位移δ21（沿P2方向）。
这里的单位力是广义单位力，位移是相应的广义位移。例如，在图14-6的两个状态中，根据位移互等定理，应有φA＝fC。实际上，由材料力学可知：
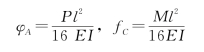(https://www.chuimin.cn)
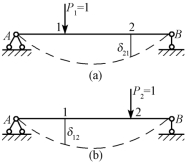
图14-5
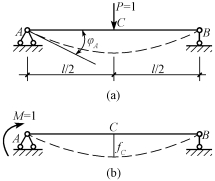
图14-6
现在P＝1、M＝1（这里的1都是不带单位的，即都是无量纲量），故有
。可见，虽然φA代表单位力引起的角位移，fC代表单位力偶引起的线位移，含义不同，但此时二者在数值上是相等的，量纲也相同。
3.反力互等定理
反力互等定理也是功的互等定理的一个特殊情况，并且只适用于超静定结构。该定理将在用位移法计算结构中得到应用。
在一个结构的诸约束中任取两个约束——约束1及约束2。在图14-7（a）所示结构中约束1是固定端中限制转角的约束，约束2是右端支杆。
考察两种状态：令约束1发生单位位移，即Δ1＝1，在支座2引起支座反力R21，此为状态1，如图14-7（a）所示；令约束2发生单位位移，即Δ2＝1，在支座1引起支座反力R12，此为状态2，如图14-7（b）所示（这里R表示单位位移引起的支座反力，第一个角标表示发生反力的地点和方向，第二个角标表示引起反力的原因）。
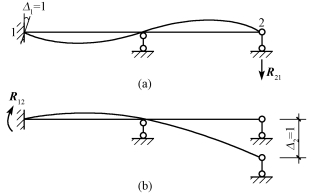
图14-7
由功的互等定理可得：
因为Δ1＝Δ2＝1，故：
式（14-13）称为反力互等定理，即支座1发生单位位移时在支座2处引起的反力（R21），等于支座2发生单位位移时在支座1处引起的反力（R12）。
需要指出的是，这里R21与R12拥有相同的量纲。这是因为它们并非一个是支杆反力，一个是反力偶，而都是约束反力与引起此反力的位移的比值，它们是反力系数，乘以位移后得反力，不拥有反力的量纲。
反力互等定理对结构上任何两个支座都适用，但应注意反力与位移在做功的关系上应相适应。力对应于线位移，力偶对应于角位移。
图14-8（a）、（b）所示为一个反力互等的例子。应用上述定理可知反力R12与反力偶R21相等，虽然它们一个代表力，一个代表力偶，两者含义不同，但在数值上是相等的。
图14-8
最后需要指出的是，上述几个互等定理，与叠加法一样，仅适用于线性弹性体系，即
（1）应力在弹性范围内，且应力与应变成正比。
（2）结构变形微小，内力可在未变形位置上计算。
相关文章
- 详细阅读
-
虚铰与瞬变体系：建筑力学第3版摘要详细阅读
图12-7所示的体系中，刚片Ⅰ在平面上本来有3个自由度，用两根不共线链杆1和2将它与基础相连接，则此体系仍有1个自由度。O点称为瞬时转动中心。这个铰称为虚铰。图12-72.瞬变体系如图12-8所示，在点A加一根水平的支座链杆1后，A点还可以移动，是几何可变体系。这种本来是几何可变的，经微小位移后又成为几何不变的体系，称为瞬变体系。瞬变体系是约束数目够用，但由于约束的布置不恰当而形成的体系。瞬变体系在工程中不能采用。......
2025-09-30
-
建筑力学研究任务和内容，建筑力学第3版详细阅读
建筑力学的任务是研究结构的几何组成规律，以及在荷载作用下结构和构件的强度、刚度和稳定性问题。具体来说，建筑力学将讨论下列几个方面的内容：力系的简化和力系平衡问题。......
2025-09-30
-
几何不变体系基本规则|建筑力学第3版详细阅读
工程结构必须采用几何不变体系，本节讨论无多余的几何不变体系的基本组成规则。无多余约束是指体系内的约束恰好使该体系称为几何不变体系。只要去掉任何一个约束就会使体系变成几何可变体系。这个几何不变体系的基本规则称为铰接三角形规则。在原体系上增加或减少若干个二元体不改变原体系的几何组成性质。由此可见，两刚片用一个铰和一根链杆相连，且链杆与此铰不共线，组成几何不变体系，且无多余约束。......
2025-09-30
-
建筑力学（第3版）：轴力图制作详细阅读
当杆件受到多于两个轴向外力的作用时，在杆件的不同横截面上轴力不尽相同。将描述沿杆长各个横截面上轴力变化规律的图形，称为轴力图。画轴力图时，将正的轴力画在轴线上方，负的轴力画在轴线下方。根据上面求出的各段杆轴力的大小及其正负号画出轴力图，如图7-6所示。画轴力图时应注意以下几点：轴力图要与计算简图对齐。标明正负号和数值。在画轴力图时，也可用一条基线表示横截面位置。......
2025-09-30
-
建筑力学第3版-平面体系几何组成分析技巧详细阅读
由基本规则分析可知，平面体系几何组成规则本身是非常简单容易理解的，都是三角形法则。那么，如何灵活利用平面结构体系几何组成基本规则，对所有纷繁复杂的平面体系进行几何组成分析，关键在于要掌握分析技巧。（二）合理选择和扩大平面杆件体系中的刚片对简化后杆件体系进行几何组成分析时，刚片的选择尤为重要，一般应遵循以下原则：首先要看简化后体系是否还存在地基，若存在直接将地基看成一个刚片，依次根据规则扩大刚片。......
2025-09-30
-
截面法求内力-建筑力学（第3版）详细阅读
图9-4求内力仍采用截面法。力Q和力偶矩M就是梁弯曲时横截面上产生的两种不同形式的内力，力Q称为剪力，力偶矩M称为弯矩。简支梁受载如图9-7所示，试用截面法求截面1—1上的内力。......
2025-09-30
- 详细阅读
相关推荐