建筑力学的任务是研究结构的几何组成规律，以及在荷载作用下结构和构件的强度、刚度和稳定性问题。具体来说，建筑力学将讨论下列几个方面的内容：力系的简化和力系平衡问题。......
2023-08-26
建筑力学（第3版）：变形体虚功原理
【摘要】：（二）变形体的虚功原理前面所讲到的简支梁，在力P1作用下会引起内力，那么，内力在其本身引起的变形上所做的功，称为内力实功，用表示；P1所做的功W11称为外力实功。计算结构位移时，需要用到的是虚力原理，不过习惯上仍称它为虚功原理，以下仍沿用这一称呼。
（一）基本概念
1.功、广义力和广义位移
由物理学可知，功与力和位移两个因素有关，功的大小等于力和位移的乘积，即
式中 P——力或力偶，称为广义力；
Δ——与广义力相应的线位移或角位移，称为广义位移。
如广义力是集中力时，广义位移为线位移；若广义力是力偶时，广义位移为转角。
功可以为正，也可以为负，还可以为零。当P与Δ方向相同时，为正；反之，则为负。若P与Δ方向相互垂直时，功为零。
2.实功与虚功
实功是指外力或内力在自身引起的位移上所做的功。如图14-2（a）所示的简支梁，设其在P1作用下达到平衡时，P1作用点沿P1方向上产生的位移为Δ11。这里Δ11用了两个角标，第一个角标“1”代表位移发生的地点和方向，即此位移是P1作用点沿P1方向上的位移；第二个角标“1”表示引起位移的原因，即此位移是由于P1作用而引起的。荷载P1在位移Δ11上所做的功W11即为实功，则
式（14-2）中含系数“
”是因为当荷载从零逐渐增大到最后值P1时，由它引起的位移从零逐渐增大到最后值Δ11，两者成线性函数关系。
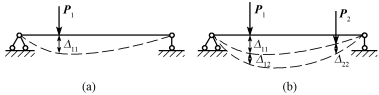
图14-2
外力（内力）在其他原因引起的位移上所做的功则称为虚功。如图14-2（b）所示，当第一组荷载P1作用于结构达到稳定平衡后，再加上第二组荷载P2，这时结构将继续变形，而引起P1作用点沿P1方向产生新的位移Δ12，因而P1将在Δ12位移上做功，这时所做的功即为虚功。由于位移Δ12由零增加至最终值的过程中，P1保持不变是常力，因此P1沿Δ12做的功为
所谓虚功并非是不存在的意思，“虚”字强调做功过程中位移与力相互独立且无关的特点。
应该指出，当其他因素引起的位移与力的方向一致时虚功为正值；反之则为负值。而实功由于力自身所引起的相应位移总是与力的作用方向相一致，故总为正值。
3.实功原理
结构受到外力作用而发生变形，则外力在发生变形过程中做了功。如果结构处于弹性阶段范围，当外力去掉后，该结构将能恢复到原来变形前的位置，这是由于弹性变形使结构积蓄了做功的能量，这种能量称为变形能。由此可见，结构之所以有这种变形，实际上是结构受到外力做功的结果，也就是功与能的转化。根据能量守恒定律可知，在加载过程中外力所做的实功W将全部转化为结构的变形能，用U表示，即
从另一个角度讲，结构在荷载作用下产生内力和变形，那么内力也将在其相应的变形上做功，而结构的变形能又可用内力所做的功来度量。这个功能原理，称为弹性结构的实功原理。
（二）变形体的虚功原理
前面所讲到的简支梁，在力P1作用下会引起内力，那么，内力在其本身引起的变形上所做的功，称为内力实功，用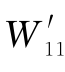
表示；P1所做的功W11称为外力实功。力P1作用下引起的内力在其他原因（如P2）引起的变形上所做的功，称为内力虚功；用
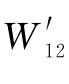表示。P1所做的功W12称为外力虚功。在该系统中，外力P1和P2所做的总功为
而P1和P2引起的内力所做的总功为
根据能量守恒定律，应有W外＝W内，即
根据实功原理，可知：
由此可得
式（14-7）又称为虚功方程。
在上述情况中，P1和P2是彼此独立无关的。P1视为第一组力先加在结构上；P2视为第二组力后加在结构上。其表明，结构的第一组外力在第二组外力所引起的位移上所做的外力虚功，等于第一组内力在第二组内力所引起的变形上所做的内力虚功。
为了便于应用，现将图14-2（b）中的平衡状态分为图14-3（a）和图14-3（b）两个状态。图14-3（a）的平衡状态称为第一状态（力状态）；图14-3（b）的平衡状态称为第二状态（位移状态）。此时，虚功原理又可以描述为：第一状态（力状态）下的外力在第二状态（位移状态）下相应的位移上所做的外力虚功，等于第一状态（力状态）下的内力在第二状态（位移状态）下相应的变形上所做的内力虚功。
图14-3
必须指出，力状态和位移状态是同一体系的两种彼此无关的状态，因此，不仅可以将位移状态看作是虚设的，也可以将力状态看作是虚设的，它们各有不同的应用。若取第一状态为实际状态，第二状态为虚拟状态，也就是虚功中力状态是实际的，位移状态是虚拟的，这时，虚功原理也称为虚位移原理；反之，若取第一状态为虚拟状态，第二状态为实际状态，也就是虚功中的力状态是虚拟的，位移状态是实际的，这时，虚功原理也称为虚力原理。计算结构位移时，需要用到的是虚力原理，不过习惯上仍称它为虚功原理，以下仍沿用这一称呼。
虚功原理既适用于静定结构，也适用于超静定结构。
有关建筑力学（第3版）的文章
- 详细阅读
-
建筑力学（第3版）-结构的计算简图详细阅读
在选取其计算简图时，可根据实际构造和约束情况进行。在计算简图中，通常可将结点分为铰结点和刚结点两种。事实上，结构在荷载作用下，杆件之间所产生的转动也相当小，所以，该结点应视为铰结点。因而，刚结点对杆端有阻止相对转动的约束力存在，既除产生杆端轴力和剪力外，还引起杆端弯矩。计算时这种结点应视为刚结点，其计算简图如图1-23所示。......
2023-08-26
- 详细阅读
-
建筑力学（第3版）：轴力图制作详细阅读
当杆件受到多于两个轴向外力的作用时，在杆件的不同横截面上轴力不尽相同。将描述沿杆长各个横截面上轴力变化规律的图形，称为轴力图。画轴力图时，将正的轴力画在轴线上方，负的轴力画在轴线下方。根据上面求出的各段杆轴力的大小及其正负号画出轴力图，如图7-6所示。画轴力图时应注意以下几点：轴力图要与计算简图对齐。标明正负号和数值。在画轴力图时，也可用一条基线表示横截面位置。......
2023-08-26
- 详细阅读
-
截面法求内力-建筑力学（第3版）详细阅读
图9-4求内力仍采用截面法。力Q和力偶矩M就是梁弯曲时横截面上产生的两种不同形式的内力，力Q称为剪力，力偶矩M称为弯矩。简支梁受载如图9-7所示，试用截面法求截面1—1上的内力。......
2023-08-26
-
荷载位置固定求量值-建筑力学第3版详细阅读
，yn，则在这组集中荷载共同作用下，量值S为应用式时，需注意竖标yi的正、负号。式表明，均布荷载引起的量值等于荷载集度乘以荷载作用段对应的影响线面积。......
2023-08-26
-
《建筑力学（第3版）》强度条件及校核详细阅读
根据以上分析，为了保证拉（压）杆在工作时不致因强度不够而破坏，杆内的最大工作应力σmax不得超过材料的许用应力[σ]，即式即拉（压）杆的强度条件。已知荷载、构件尺寸及材料的许用应力，根据强度条件校核是否满足强度要求。已知构件的横截面面积及材料的许用应力，根据强度条件可以确定杆能承受的最大轴力，即从而即可求出承载力。......
2023-08-26
相关推荐