静定平面刚架的内力计算同梁一样，仍是用截面法截取隔离体，然后用平衡条件求解。根据荷载情况，将刚架分解成若干杆段，由平衡条件求出杆端内力。该杆上作用有一集中荷载，可以分为CE和EB两个无荷载区段，用截面法求出下列控制截面的弯矩：便可以绘制出该杆弯矩图。根据荷载和已经求出的反力，可以用截面法求出杆件各个控制截面的剪力和轴力，从而绘制出整个钢架的剪力图和轴力图，如图12-18、所示。......
2025-09-29
桁架内力计算方法及应用案例
【摘要】：桁架的内力计算方法有节点法、截面法、联合法。桁架中某杆的轴力为零时，此杆称为零杆。图13-16试用节点法计算图13-17所示桁架的各杆内力。求图13-19所示桁架1、2、3杆的内力N1、N2、N3。如图13-20所示，欲求图中a杆的内力，如果只用节点法计算，无论取哪个节点为隔离体，都有三个以上的未知力，无法直接求解；如果只用截面法计算，也需要解联立方程。宜联合应用节点法和截面法，求所需反力和指定杆件内力。
桁架的内力计算方法有节点法、截面法、联合法。计算桁架内力的基本方法仍然是先取隔离体，然后根据平衡方程求解，即所求内力。当所取隔离体仅包含一个节点时，这种方法称为节点法；当所取隔离体包含两个或两个以上节点时，这种方法称为截面法；节点法与截面法联合应用的方法，称为联合法。
1.节点法计算桁架杆件内力
节点法是以桁架节点为研究对象（也称隔离体），由节点平衡条件求杆件内力的方法。每一个平面桁架的节点受平面汇交力系的作用，可以并且只能列两个独立的平衡方程。因此，在所取节点上，未知内力的个数不能超过两个。在求解时，应先截取只有两个未知力的节点，依次逐点计算，即可求得所有杆件的内力。计算时，通常先假设未知杆件内力为拉力（拉力的指向是离开节点），若计算结果为正即为拉力；反之，表示轴力为压力。
桁架中某杆的轴力为零时，此杆称为零杆。计算时宜先判断出零杆，使计算得以简化。常见的零杆有以下几种情况：
（1）不共线的两杆节点，若无外力作用，则此两杆轴力必为零，如图13-16（a）所示。
（2）不共线的两杆节点，若外力与其中一杆共线，则另一杆轴力必为零，如图13-16（b）所示。
（3）三杆节点，无外力作用，若其中两杆共线，则另一杆轴力必为零，如图13-16（c）所示。
图13-16
【例13-6】 试用节点法计算图13-17（a）所示桁架的各杆内力。
【解】 （1）求支座反力。由于无水平外力作用，故水平反力RAx＝0。可由对称性判断RAy＝RB＝2P（↑）
（2）求内力。由对称性判断
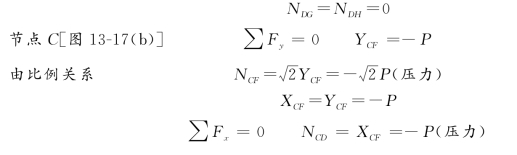
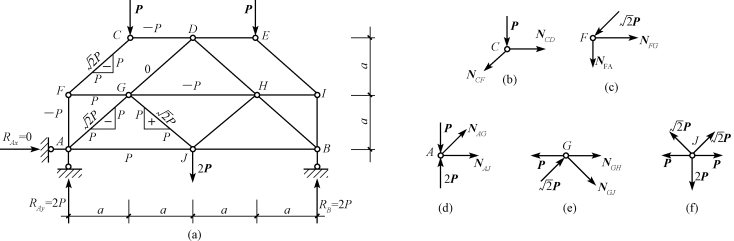
图13-17
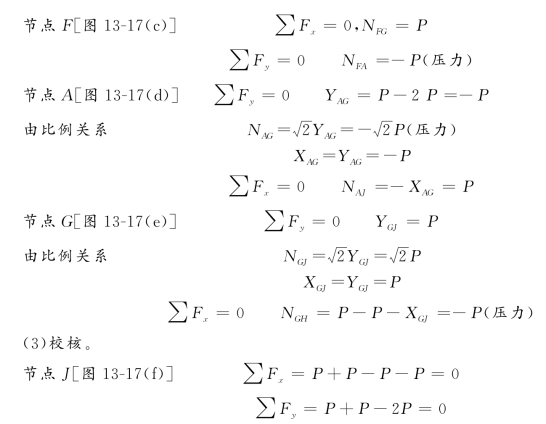
节点J满足平衡条件，故知计算正确。
在图示荷载作用下，内力为对称分布，只需计算半个桁架，各杆轴力示于图13-17（a）中。
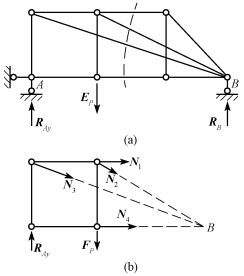
图13-18
2.截面法计算桁架杆件内力
截面法就是假想用一个截面将桁架分成两部分，取其中一部分为隔离体。隔离体受平面一般力系的作用，由三个独立的平衡方程可求得所切各杆的未知轴力。通常，截面所切断的杆件个数不应超过三个。有时，被截杆件虽然超过三个，但某些杆件的轴力仍能由此隔离体求出。图13-18所示的截面，虽然截了四根杆，但除第一根杆外，均交于点B，由
＝0可求出N1。
【例13-7】 求图13-19（a）所示桁架1、2、3杆的内力N1、N2、N3。
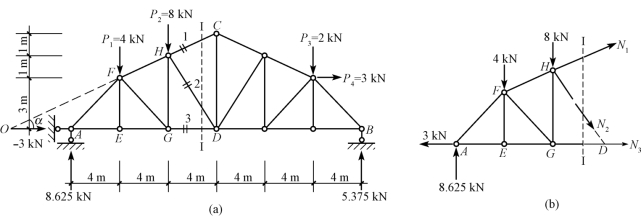
图13-19(https://www.chuimin.cn)
【解】 （1）求支座反力：
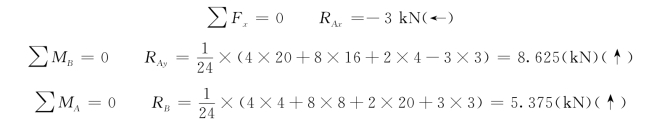
（2）求内力。利用截面Ⅰ—Ⅰ将桁架截断，以左段为研究对象，受力图如图13-19（b）所示。则由
得
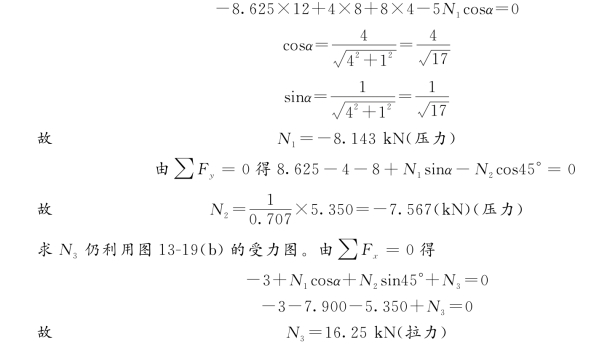
（3）校核。用图13-19（b）中未用过的力矩方程
＝0进行校核。
3.联合法计算桁架杆件内力
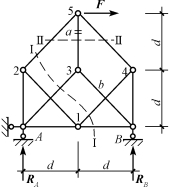
图13-20
对于一些简单桁架，单独使用节点法或截面法求解各杆内力是可行的，但是对于一些复杂桁架和联合桁架，将节点法和截面法联合起来使用则更方便。如图13-20所示，欲求图中a杆的内力，如果只用节点法计算，无论取哪个节点为隔离体，都有三个以上的未知力，无法直接求解；如果只用截面法计算，也需要解联立方程。为简化计算，可以先作截面Ⅰ—Ⅰ，取右半部分为隔离体，由于被截的四杆中，有三杆平行，故可先求1B杆的内力；然后，以节点B为隔离体，可较方便地求出3B杆的内力；再以节点3为隔离体，即可求得a杆的内力。
【例13-8】 试计算图13-21（a）所示桁架指定杆件的内力。
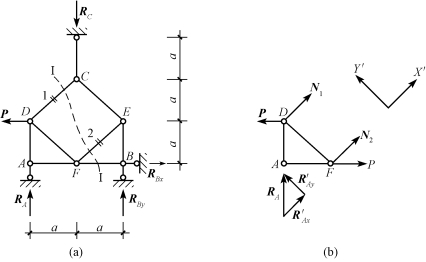
图13-21
【解】 本例为联合桁架，属于三刚片结构，不能由整体平衡条件求得全部反力。宜联合应用节点法和截面法，求所需反力和指定杆件内力。
在截面Ⅰ—Ⅰ以左的隔离体上，包含RA、N1、N2三个未知力。其中，N1和N2为两平行力。选择垂直于N1和N2的投影轴，建立独立的投影方程，求得R′Ax和R′Ay后，则易求解N1和N2。
（1）求水平反力。由整体平衡条件：
（2）求内力。
节点B
截面Ⅰ－Ⅰ左[图13-21（b）]
故
相关文章
- 详细阅读
-
图形面积计算方法及应用详细阅读
我们如果只凭直观感受进行判断,那么很可能产生错觉或错误的判断,我们把看上去的情况和实际有偏差的图形,称之为错视图形．知能概述面积是平面几何中一个重要概念,计算图形面积是平面几何中最基本的问题之一,常用的计算方法有:和差法、运动法、等积变形法．面积的计算主要是求一些非常规图形的面积,非常规图形面积的计算往往可转化为常规图形面积的计算．在转化的过程中,常用到恰当连线、图形割补、等积变形、线段比与面积比......
2025-09-29
-
常用的位逻辑指令及应用案例分析详细阅读
表5-1 常用的位逻辑指令1.基本逻辑指令常开触点对应的存储器地址位为1状态时，该触点闭合。当I0.2=1，I0.3=1时，Q4.0～Q4.7被复位为零。图5-4 置位域复位域指令图5-5 触发器的置位复位指令触发器指令上的M0.0和M0.1称为标志位，R、S输入端首先对标志位进行复位和置位，然后再将标志位的状态送到输出端。编写程序如图5-12所示，其中M1.5为CPU时钟存储器MB1的第5位，其时钟频率为1 Hz。......
2025-09-29
-
变频器在实际应用中的作用及应用案例详细阅读
可编程序控制器、变频器、伺服电机、人机界面是驱动控制系统中不可缺少的组成部分。通常，纺织机械系统中的电动机普遍采用通用变频器控制，所有的变频器则统一由PLC控制。图解演示例如，图11-35所示变频器在电梯智能控制中的应用。图11-35 变频器在电梯智能控制中的应用5.变频器在民用改善环境中的应用随着人们对生活质量和环境的要求不断提高......
2025-09-29
-
弧长和扇形面积的计算方法及应用详细阅读
在半径为R的圆中，n°的圆心角所对的弧长的计算公式为l＝________；如果扇形的半径为R，圆心角为n°，那么扇形面积的计算公式为S扇形＝_________；如果扇形的半径为R，所对的弧长为l，那么扇形面积的计算公式为S扇形＝________．（第2题）（第3题）3．扇子是引风用品，夏令营必备之物，纸扇在DE与BC之间糊有纸（扇面），可以题字或者作画．如图，竹条AD的长为5cm，贴纸的部分BD的......
2025-09-29
-
常用工控机简介及应用案例详细阅读
PC总线工业电脑据2000年IPC统计，目前工控机已占到通用计算机的95%以上，因其价格低、质量高、产量大、软／硬件资源丰富，已被广大的技术人员所熟悉和认可，这正是工业电脑热的基础。如图5－18所示，工控机主要的组成部分为工业机箱、无源底板及可插入其上的各种板卡组成，如CPU卡、I／O卡等。图5－19两种不同的PLC实物图图5－20所示为PLC应用于逻辑控制的简单例子。......
2025-09-29
-
兴利调节计算方法应用指南详细阅读
G4.7.1.1列表法调节计算调节计算时一般不用日历年，而采用水利年，即以水库蓄泄过程的循环作为一年的起讫点。表G4.7列表法年调节计算单位：万m3当余、亏水段多于两个时，称为多回运用。兴利调节计算中，把最大累积亏水量对应的时期称为集中供水期，简称供水期。［例G4.3］中供水期为12月至次年6月共7个月；［例G4.4］供水期为11月至次年6月共8个月。......
2025-09-29
-
配置计算方法与应用详解详细阅读
不少学者结合当前发展需求和新技术研究了水资源系统配置的一些理论和方法。甘泓等结合新疆水资源配置研究，给出了水资源配置的目标量度和分配机制，提出了水资源配置动态模拟模型，开发了相应的决策支持系统，研制出可适用于巨型水资源系统的智能型模拟模型。从计算方法分析，随着数值分析与计算机应用水平的提高，水资源配置中逐渐引入了优化和模拟两种计算方法。......
2025-09-29
相关推荐