在实际的建筑工程中，多跨静定梁常用来跨越几个相连的跨度。图12-9桥梁在房屋建筑结构中的木檩条[图12-10]，也是多跨静定梁的结构形式。图12-10木檩条从几何组成来看，多跨静定梁可分为基本部分和附属部分。但是从整体看，多跨静定梁是几何不变的，也是静定的。因此，一般来说，多跨静定梁的弯矩比一列简支梁的弯矩小，所用材料较为节省。但是，多跨静定梁的构造较为复杂。......
2023-06-16
多跨静定梁在建筑工程中的应用及优势
【摘要】：在实际的建筑工程中，多跨静定梁常用来跨越几个相连的跨度。图13-1所示为在公路或城市桥梁中常采用的多跨静定梁结构形式之一。因而，系列简支梁虽然结构较简单，但多跨静定梁的承载能力大于系列简支梁，在同样荷载的情况下可节省材料，但其构造要复杂些。
1.多跨静定梁的几何组成
多跨静定梁是由若干根伸臂梁和简支梁用铰连接而成的，并用来跨越几个相连跨度的静定梁。在实际的建筑工程中，多跨静定梁常用来跨越几个相连的跨度。图13-1（a）所示为在公路或城市桥梁中常采用的多跨静定梁结构形式之一。其计算简图如图13-1（b）所示。
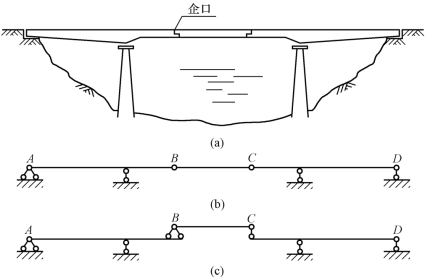
图13-1
在房屋建筑结构中的木檩条，也是多跨静定梁的结构形式。连接单跨梁的一些中间铰，在钢筋混凝土结构中，其主要形式常采用企口结合[图13-1（a）]，而在木结构中常采用斜搭接并用螺栓连接。
从几何组成分析可知，图13-1（b）中AB梁直接由链杆支座与地基相连，是几何不变的，且梁AB本身不依赖梁BC和CD就可以独立承受荷载，称为基本部分。如果仅受竖向荷载作用，CD梁也能独立承受荷载维持平衡，同样可视为基本部分。短梁BC依靠基本部分的支承才能承受荷载并保持平衡，所以称为附属部分。为了更清楚地表示各部分之间的支承关系，将基本部分画在下层，将附属部分画在上层，如图13-1（c）所示，称为关系图或层次图。
多跨静定梁按其几何组成特点可分为两种基本形式，第一种基本形式如图13-2（b）所示，其中第一、三、五跨为基本部分，第二、四等跨为附属部分，它通过铰与两侧相邻的基本部分相连；第二种基本形式如图13-2（c）所示，第一跨为基本部分，而第二、三、四等跨分别为其左边各跨的附属部分，即各附属部分的附属程度由左至右逐渐增高。其层次图如图13-2（d）所示。
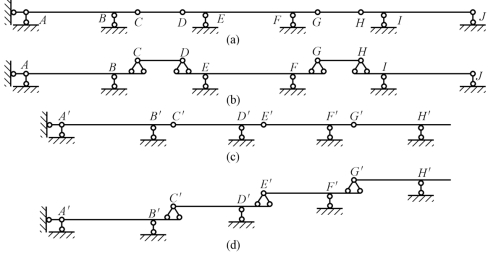
图13-2
2.多跨静定梁的内力计算
由层次图可见，作用于基本部分上的荷载，并不影响附属部分，而作用于附属部分上的荷载，会以支座反力的形式影响基本部分，因此，在多跨静定梁的内力计算时，应先计算高层次的附属部分，后计算低层次的附属部分；然后，将附属部分的支座反力反向作用于基本部分，计算其内力；最后，将各单跨梁的内力图连成一体，即为多跨静定梁的内力图。
【例13-1】 作图13-3（a）所示梁的弯矩图。
【解】 切断铰C、F即可以看出中间部分CDEF是基本部分，两侧部分是附属部分，层次图如图13-3（b）所示。
先计算附属梁[图13-3（c）]。这是一个单跨梁计算问题，求得支座反力及弯矩图如图13-3（c）所示。
将附属梁的相应支座反力反其方向作用于基本梁上[图13-3（d）]，算得基本梁的支座反力如图13-3（d）所示。绘得弯矩图如图13-3（e）所示。弯矩图是用叠加法绘制的：先计算出MDC＝ql·
，下拉；
，上拉。引基线，再叠加上分布荷载在简支梁上引起的弯矩图。
将各梁的弯矩图合并，即得全梁的弯矩图[图13-3（f）]；铰C、F处弯矩应为零。BCD段上弯矩图应为一条直线，因为在此段上无外载作用。同理，EFH段上弯矩图也应为一条直线。
同样，可先绘制各梁的剪力图，然后合并成全梁的剪力图[图13-3（g）]。在BCD段上剪力图为一常数，因为在此段上无外载作用。铰C处有剪力。EFH段也类似。
在图13-3（c）上未画出水平支杆，是为了表明轴力是静定的，而且等于零。
3.多跨静定梁的受力特征
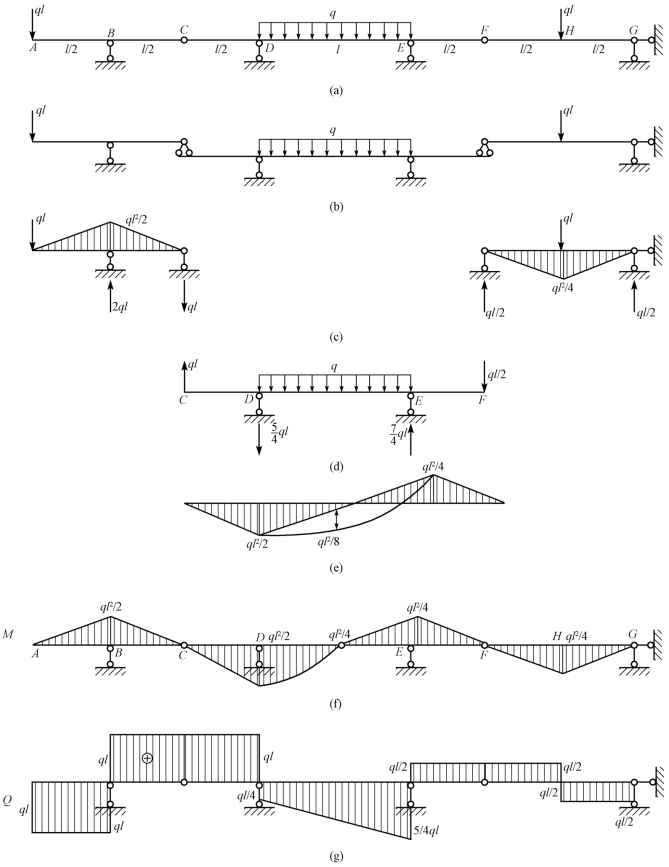
图13-3
图13-4是多跨静定梁及其在均布荷载q的作用下的弯矩图，图13-5是一相同支座间距、相同荷载作用下的系列简支梁及其弯矩图。比较两个弯矩图可以看出，系列简支梁的最大弯矩大于多跨静定梁的最大弯矩，多跨静定梁的弯矩分布比较均匀，中间支座处有负弯矩，由于支座负弯矩的存在，减少了跨中的正弯矩。因而，系列简支梁虽然结构较简单，但多跨静定梁的承载能力大于系列简支梁，在同样荷载的情况下可节省材料，但其构造要复杂些。
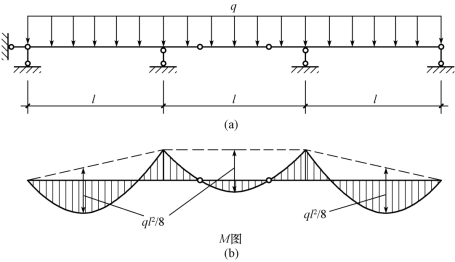
图13-4
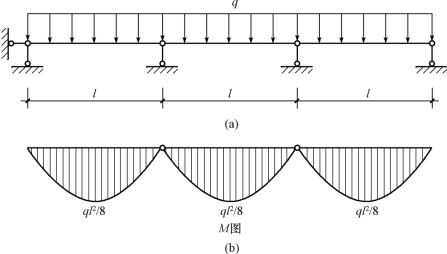
图13-5
有关建筑力学（第3版）的文章
- 详细阅读
-
3.2结构力学：多跨静定梁的内力计算详细阅读
图3-6多跨静定梁是由若干单跨静定梁相互用铰连接起来的，通常有两种基本形式。图3-82.多跨静定梁的内力计算从受力分析来看，由于基本部分直接与地基组成几何不变体系，因此它能独立承受荷载而维持平衡。......
2023-08-30
-
单跨静定梁内力分析方法及其应用详细阅读
单跨静定梁在实际工程中应用较多，例如一般钢筋混凝土过梁、起重机梁等，其内力分析方法已在第六章中作了详细介绍。作内力图时，轴力图、剪力图要注明正负号，弯矩图规定画在杆件受拉的一侧，不用注明正负号。由于图12-7所示两个微段荷载应为等值，故有qdx＝q′ds由此可得图12-7斜梁上荷载沿轴线方向分布单跨斜梁的内力除了弯矩和剪力之外，还有轴向力。......
2023-06-16
-
MATLAB在时域分析中的优势及应用案例介绍详细阅读
本节将主要介绍如何利用MATLAB软件来分析线性控制系统的稳定性、输入响应及性能指标。下面给出时域分析时常用的MATLAB命令。例3-11 已知闭环系统传递函数为试用MATLAB判断系统的稳定性。图3-30例3-12系统的阶跃响应曲线图3-31例3-12系统的脉冲响应曲线例3-13 已知单位负反馈控制系统的开环传递函数为，试用MATLAB计算系统在单位阶跃信号作用下的tr、tp、ts、σ%。......
2023-06-28
-
梁的强度条件在实际工程中的应用详细阅读
在梁的强度计算中，必须同时满足正应力和剪应力两个强度条件。通常先按正应力强度条件设计出截面尺寸，然后按剪应力强度条件进行校核。但在以下几种情况下，需校核梁的剪应力：①最大弯矩很小而最大剪力很大的梁；②焊接或铆接的组合截面梁；③木梁，因为木材在顺纹方向的剪切强度较低，所以木梁有可能沿中性层发生剪切破坏。按强度条件求许用荷载[F]。......
2023-06-16
-
纳米压痕技术在应用中的优势和挑战详细阅读
近十几年来，在微观力学方面，纳米压痕技术受到越来越广泛的应用，主要体现在以下几个方面。图6-27为采用纳米压痕技术在硅表面施加50mN压力后形成的压痕阵列。图6-30为利用纳米压痕和显微成像技术相结合的一个典型例子。图6-31为采用材料纳米压痕技术测量Al多晶材料中一个晶粒性能的过程及力—位移曲线。Bahr［88］利用纳米压痕实验完成了低于50 nm深度的硬度测量；Adams［89］用纳米压痕实验研究了颗粒薄膜凝聚体的断裂机制。......
2023-06-20
-
CAE在推广和应用设计中的优势详细阅读
可是，事实上，却很少在国内发现有推广设计CAE的优秀事例。不从认识上消除这些担心，就难以在设计现场推广应用CAE，这也是没有引进设计CAE的一个原因。现在本田大量地采用了设计CAE，实现了从KKD设计到设计CAE的转变。在领导人员认识和理解了设计CAE的重要性和优越性以后，问题就成功了一半。特别要注意采用那些设计人员易于熟悉的工具，如与CAD系统集成的CAE工具。......
2023-06-21
-
专业化在信息处理中的优势及应用详细阅读
专业化大脑的功能就是用来处理信息，所以我们需要考虑信息处理系统中特异化的权衡和优势。没有任何关于专业化的信息来源能说明这些信息对于建造一个能正确运行的机器是必需的。不仅仅是计算机科学家，我认为苹果公司iPhone手机的成功很大程度上就是来自于iPhone手机上运行了大量专业化的小程序。iPhone手机被广泛地使用，就是因为它可以运行很多和模块类似的实用性应用程序。......
2024-03-04
相关推荐