在第一章中，已对几何法进行了介绍，知道了两个汇交于一点的力F1和F2如何应用力的平行四边形法则和三角形法则求它们的合力R。设作用于物体上A点的力F1、F2、F3、F4组成平面汇交力系，现求其合力，如图2-2所示。这种由各分力和合力构成的多边形abcde称为力多边形。这种求合力矢的几何作图法被称为力多边形法。拉力F1、F2、F3的作用力汇交于O点，构成平面汇交力系。......
2025-09-30
平面体系几何组成分析在建筑力学中的应用
【摘要】：根据组成几何不变体系的基本规则对体系进行几何组成分析。作几何组成分析时，为了使分析过程简化，应注意以下两点：可将体系中的几何不变部分当作一个刚片来处理。则连接三刚片的三个铰A、B、O不在一直线上，符合三刚片规则，故体系为几何不变且无多余约束。CDE和基础视为两刚片，两刚片用三根链杆1、链杆2、链杆3相连，此三根链杆汇交于同一点，所以体系为几何可变体系。
根据组成几何不变体系的基本规则对体系进行几何组成分析。作几何组成分析时，为了使分析过程简化，应注意以下两点：
（1）可将体系中的几何不变部分当作一个刚片来处理。
（2）逐步拆去二杆结点，这样做并不影响原体系的几何组成性质。
下面举例说明如何应用组成几何不变体系的基本规则对体系进行几何组成分析。
【例12-1】 试对图12-16所示的体系进行几何组成分析。
图12-16
【解】 AB杆与基础之间用铰A和链杆1相连，组成几何不变体系，可看作是一个扩大了的刚片。将BC杆看作链杆，则CD杆用不交于一点的三根链杆BC、2、3和扩大刚片相连，组成无多余约束的几何不变体系。
【例12-2】 对图12-17所示的体系进行几何组成分析。
(https://www.chuimin.cn)
图12-17
【解】 以三角形ABC和BDE分别为大刚片Ⅰ和刚片Ⅱ，链杆1与链杆2相当于瞬铰F，链杆3与链杆4相当于瞬铰G，如果F、B、G三铰不共线，则体系为无多余约束的几何不变体系。
【例12-3】 对图12-18所示的体系进行几何组成分析。
【解】 将图12-18中的AC、BD、基础分别视为刚片Ⅰ、刚片Ⅱ、刚片Ⅲ，刚片Ⅰ和刚片Ⅲ以铰A相连，刚片Ⅱ和刚片Ⅲ用铰B连接，刚片Ⅰ和刚片Ⅱ是用CD、EF两链杆相连，相当于一个虚铰O。则连接三刚片的三个铰A、B、O不在一直线上，符合三刚片规则，故体系为几何不变且无多余约束。
图12-18
【例12-4】 分析图12-19所示体系的几何组成。
【解】 将折杆AC和BD分别用虚线表示的链杆2、链杆3来替换。CDE和基础视为两刚片，两刚片用三根链杆1、链杆2、链杆3相连，此三根链杆汇交于同一点，所以体系为几何可变体系。
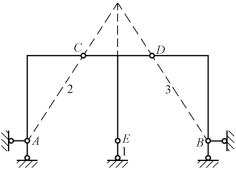
图12-19
相关文章
- 详细阅读
-
建筑力学：平面平行力系平衡方程详细阅读
如前所述，力系中各力的作用线在同一平面内且相互平行，这样的力系称为平面平行力系。平面汇交力系、平面力偶系、平面平行力系都是平面任意力系的特殊情况。下面导出平面平行力系的平衡方程。于是，平面平行力系只有两个独立的平衡方程，即图4-8平面平行力系的平衡方程，也可以写成二力矩式的形式，即式中，A、B两点的连线不与力线平行。利用平面平行力系的平衡方程，可求解两个未知量。......
2025-09-30
-
力的等效平移原理及其在建筑力学中的应用详细阅读
由此可得力的平移定理：作用在刚体上A点的力F可以等效地平移到此刚体上的任意一点B，但必须附加一个力偶，附加力偶的力偶矩等于原来的力F对新的作用点B的矩。力P与柱轴线的距离为e，称为偏心距。按力的平移定理，可将力P等效地平移到立柱的轴线上，同时附加一力偶矩m＝－Pe，如图4-2所示。说明力P所引起的变形是压缩和弯曲两种变形的组合。......
2025-09-30
-
建筑力学中荷载的概念及分类详细阅读
根据荷载的分布范围分类。由于这种荷载的分布面积较集中，因此，在计算简图上可将这种荷载作用于结构上的某一点处。若荷载连续作用各处大小相同，这种荷载称为均布荷载。根据荷载的作用性质分类。动力荷载的特点是该荷载作用在结构上时，会产生惯性力，从而引起结构显著的振动或冲击。......
2025-09-30
-
建筑力学第五节：物体系统的平衡详细阅读
图4-13求解物体系统的平衡问题具有重要的实际意义。当物体系统处于平衡状态时，该体系中的每一个物体也必定处于平衡状态。对由n个物体组成的物体系统，则共有3n个独立的平衡方程。假如物体系统中有受平面汇交力系或平面平行力系作用的物体，独立的平衡方程数目相应减少。按照上述方法求解物体系统的平衡问题，在理论上并不困难。求解物体系统的平衡问题，关键在于恰当地选取研究对象，正确地选取投影轴和矩心，列出适当的平衡方程。......
2025-09-30
-
水力学法在水文分析中的应用及原理详细阅读
水力学法包括湿周法、R2-Cross法等，其原理主要通过水力学现场数据，分析河流流量与鱼类栖息地指示因子的关系。表4.2采用R2-Cross单断面法确定最小流量的标准......
2025-09-30
-
虚铰与瞬变体系：建筑力学第3版摘要详细阅读
图12-7所示的体系中，刚片Ⅰ在平面上本来有3个自由度，用两根不共线链杆1和2将它与基础相连接，则此体系仍有1个自由度。O点称为瞬时转动中心。这个铰称为虚铰。图12-72.瞬变体系如图12-8所示，在点A加一根水平的支座链杆1后，A点还可以移动，是几何可变体系。这种本来是几何可变的，经微小位移后又成为几何不变的体系，称为瞬变体系。瞬变体系是约束数目够用，但由于约束的布置不恰当而形成的体系。瞬变体系在工程中不能采用。......
2025-09-30
-
平面几何分析的组成结构详细阅读
对一个平面体系进行几何组成分析时，其可能的最终结果共有四种情况：几何不变体系，且无多余约束；几何不变体系，且有多余约束；常变体系；瞬变体系。在进行平面体系的几何组成分析时，一定要注意每根杆件使用且只能使用一次。由三刚片规则可知，它们所组成的体系是几何不变体系，并且没有多余约束。试对图11-24所示的体系进行几何组成分析。......
2025-09-29
相关推荐