根据组成几何不变体系的基本规则对体系进行几何组成分析。作几何组成分析时，为了使分析过程简化，应注意以下两点：可将体系中的几何不变部分当作一个刚片来处理。则连接三刚片的三个铰A、B、O不在一直线上，符合三刚片规则，故体系为几何不变且无多余约束。CDE和基础视为两刚片，两刚片用三根链杆1、链杆2、链杆3相连，此三根链杆汇交于同一点，所以体系为几何可变体系。......
2023-08-26
建筑力学第3版-平面体系几何组成分析技巧
【摘要】：由基本规则分析可知，平面体系几何组成规则本身是非常简单容易理解的，都是三角形法则。那么，如何灵活利用平面结构体系几何组成基本规则，对所有纷繁复杂的平面体系进行几何组成分析，关键在于要掌握分析技巧。（二）合理选择和扩大平面杆件体系中的刚片对简化后杆件体系进行几何组成分析时，刚片的选择尤为重要，一般应遵循以下原则：首先要看简化后体系是否还存在地基，若存在直接将地基看成一个刚片，依次根据规则扩大刚片。
由基本规则分析可知，平面体系几何组成规则本身是非常简单容易理解的，都是三角形法则。但由于实际中的结构体系是千变万化的，每个体系的组成形式也各不相同。那么，如何灵活利用平面结构体系几何组成基本规则，对所有纷繁复杂的平面体系进行几何组成分析，关键在于要掌握分析技巧。
几何不变体系判定规则的缺陷探讨
（一）对平面杆件体系进行简化分析
简化体系，可使体系简单明了，为进一步分析排除干扰，但不改变体系的几何性质，对平面杆件体系进行简化分析，常用以下三种简化方法：
（1）结构的等效替换，其包括折杆、曲杆等效替换成直杆，内部没有多余约束的几何不变体等效成直杆，支座等效替换。在图12-12（a）所示平面体系中，折杆AB可用直杆AB等效替代，曲杆CD可以用直杆CD来等效替代。图12-12（b）所示体系内部没有多余约束的几何不变体BCDEF部分，等效替换成直杆BC，很容易利用平面体系几何组成规则判断图12-12（a）和图12-12（b）所示体系都为无多余约束的几何不变体。图12-12（c）所示体系几何组成分析时很不容易分析出结果，但是将A支座进行等效替换后，取体系中几何不变体EFC为刚片Ⅰ，取杆DB为刚片Ⅱ，地基为刚片Ⅲ，体系符合三角形刚片的组成原则，为无多余约束的几何不变体系。
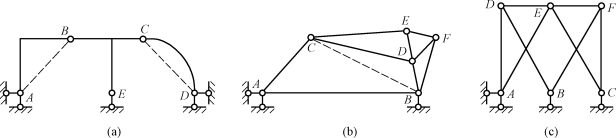
图12-12
（2）拆除体系中的独立二元体或连续拆除体系中的二元体。如图12-13（a）所示，将暴露的二元体GHE，FGE，DFE，DEC，ADC，ACB依次去掉后，就剩余梁AB（杆AB和地基），很容易判断平面体系为有一个多余约束的几何不变体系，同理可以判定图12-13（b）所示为无多余约束的几何不变体系。
图12-13
（3）若地基与体系只由一铰一链杆相连，且链杆不过铰（简支支承），则可将地基拆除掉；若地基约束超过3个，可将地基直接看成一个刚片，如图12-13（c）所示，去掉地基约束（由一铰一链杆相连，且链杆不过铰之后），一次去掉暴露的二元体ACB，CFG，CDE，DBH，EDH，EHG后，很容易判断其无多余约束的几何不变体系。
（二）合理选择和扩大平面杆件体系中的刚片
对简化后杆件体系进行几何组成分析时，刚片的选择尤为重要，一般应遵循以下原则：
（1）首先要看简化后体系是否还存在地基（大于3个约束），若存在直接将地基看成一个刚片，依次根据规则扩大刚片。
（2）对体系中的杆件或几何不变体看作一个刚片，依次扩大刚片。如图12-14（a）所示，去掉基础，将几何不变体ADC作为刚片Ⅰ，几何不变体CEB当作刚片Ⅱ，刚片Ⅱ和刚片Ⅲ通过杆DE和铰C连接。因此，体系为无多余约束的几何不变体系。图12-14（b）中，将地基看成刚片Ⅰ，ACD当作刚片Ⅱ，DEB当作刚片Ⅲ，三刚片用三个铰A、B、D连接，符合三角形规则，组成无多余约束的几何不变体Ⅰ，继续依次加二元体CFG、GHD、HIE、IJK，因此，体系为无多余约束的几何不变体。
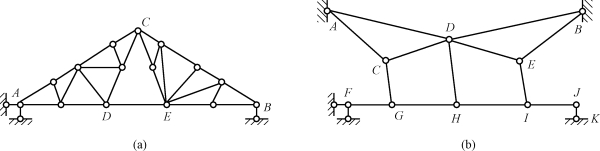
图12-14
（3）对称结构（含有部分对称结构）分散选择刚片，图12-15（a）所示为对称结构，去掉地基后，分散选取刚片，取杆AE为刚片Ⅰ，杆DF为刚片Ⅱ，杆CB为刚片Ⅲ，刚片Ⅰ和刚片Ⅱ通过杆ED和杆AF连接交于G点，刚片Ⅱ和刚片Ⅲ通过杆CD和杆FB连接交于K点，刚片Ⅰ和刚片Ⅲ通过杆AC和杆EB连接交于L点，可以判定该体系为无多余约束的几何不变体。图12-15（b）体系去掉二元体CED，先分析体系中对称结构FGHKIJ部分，依据上述分散取干片法可以判定为无多余约束的几何不变体——刚片Ⅰ，地基为刚片Ⅱ，几何不变体AECD为刚片Ⅲ，刚片Ⅰ和刚片Ⅱ通过杆CD和杆EF连接交于无穷远处一点为M，刚片Ⅰ和刚片Ⅲ通过杆1和杆2连接交于J点，刚片Ⅱ和刚片Ⅲ通过铰A连接，可以判定体系为无多余约束的几何不变体。
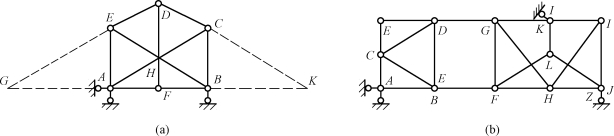
图12-15
有关建筑力学（第3版）的文章
- 详细阅读
-
结构力学：平面体系几何组成分析实例详细阅读
利用组成几何不变体系的基本规则，可以组成各种各样的几何不变体系，也可以利用这些规则对已有的体系进行几何组成分析。下面将通过具体的例子来说明平面体系的几何组成分析。两刚片由铰 C 和杆 IJ 连接，根据规则 2 可知，体系为几何不变体，且无多余约束，作为一个大刚片。 试对图 2-16所示体系做几何组成分析。如果铰B 和虚铰O1、O2不在同一条直线上，则此体系为无多余约束的几何不变体系；如果此三铰在同一条直线上，则为瞬变体系。......
2023-08-30
-
建筑力学第3版：平面汇交力合成几何法详细阅读
在第一章中，已对几何法进行了介绍，知道了两个汇交于一点的力F1和F2如何应用力的平行四边形法则和三角形法则求它们的合力R。设作用于物体上A点的力F1、F2、F3、F4组成平面汇交力系，现求其合力，如图2-2所示。这种由各分力和合力构成的多边形abcde称为力多边形。这种求合力矢的几何作图法被称为力多边形法。拉力F1、F2、F3的作用力汇交于O点，构成平面汇交力系。......
2023-08-26
-
几何不变体系基本规则|建筑力学第3版详细阅读
工程结构必须采用几何不变体系，本节讨论无多余的几何不变体系的基本组成规则。无多余约束是指体系内的约束恰好使该体系称为几何不变体系。只要去掉任何一个约束就会使体系变成几何可变体系。这个几何不变体系的基本规则称为铰接三角形规则。在原体系上增加或减少若干个二元体不改变原体系的几何组成性质。由此可见，两刚片用一个铰和一根链杆相连，且链杆与此铰不共线，组成几何不变体系，且无多余约束。......
2023-08-26
-
建筑力学第3版：平面汇交力系平衡条件解析详细阅读
几何法求解平面汇交力系的合力具有直观、明了、简捷的优点，但其精确度较差，在力学计算时多用解析法。物体在平面汇交力系作用下处于平衡的充分必要条件是：合力R的大小等于零。即要使式（2-8）成立，则：式（2-9）表明平面汇交力系平衡的解析条件是：力系中各分力在任意两个坐标轴上投影的代数和分别等于零。式（2-9）称为平面汇交力系的平衡方程。代入相应数据解得负号表示受力图中的方向与实际相反，在斜杆中实为压力。......
2023-08-26
-
建筑力学研究任务和内容，建筑力学第3版详细阅读
建筑力学的任务是研究结构的几何组成规律，以及在荷载作用下结构和构件的强度、刚度和稳定性问题。具体来说，建筑力学将讨论下列几个方面的内容：力系的简化和力系平衡问题。......
2023-08-26
-
静定平面刚架内力计算方法(建筑力学第3版)详细阅读
静定平面刚架的内力包括弯矩、剪力与轴力。根据前述内力图绘制法逐杆绘制刚架的内力图，并进行校核。求支座反力时要根据支座的性质定出支座反力未知量的个数，然后假定反力方向，由平衡方程确定其数值。求图13-9所示刚架的支座反力。（二）刚架杆截面内力的计算1.刚架内力正负号的规定刚架的内力有弯矩、剪力和轴力。如杆端截面C1、C2的弯矩分别用MCA、MCD表示，剪力和轴力分别用QCA、QCD和NCA、NCD表示。......
2023-08-26
-
虚铰与瞬变体系：建筑力学第3版摘要详细阅读
图12-7所示的体系中，刚片Ⅰ在平面上本来有3个自由度，用两根不共线链杆1和2将它与基础相连接，则此体系仍有1个自由度。O点称为瞬时转动中心。这个铰称为虚铰。图12-72.瞬变体系如图12-8所示，在点A加一根水平的支座链杆1后，A点还可以移动，是几何可变体系。这种本来是几何可变的，经微小位移后又成为几何不变的体系，称为瞬变体系。瞬变体系是约束数目够用，但由于约束的布置不恰当而形成的体系。瞬变体系在工程中不能采用。......
2023-08-26
相关推荐