欧拉公式的适用范围。欧拉公式是根据曲线近似微分方程导出的，应用此微分方程时，材料必须服从胡克定律。因此，欧拉公式的适用范围应当是压杆的临界应力σcr，不超过材料的比例极限σP，即λP为压杆的临界应力达到材料的比例极限时的柔度值，即则欧拉公式的适用范围为式（9-5）表明，当压杆的柔度λ 不小于λP 时，才可以应用欧拉公式计算临界力或临界应力。这类压杆称为大柔度杆或细长杆，欧拉公式只适用于较细长的大柔度杆。......
2023-06-19
欧拉公式适用范围-建筑力学（第3版）
【摘要】：由于欧拉公式是假设材料在线弹性范围内的条件下，根据挠曲线近似微分方程导出的，而应用此微分方程时，材料必须适用胡克定律。故欧拉公式的适用范围是：临界应力σcr不超过材料的比例极限。即有若设λP为压杆的临界应力达到材料的比例极限σP时的柔度值，则故欧拉公式的适用范围为式表明，当压杆的柔度不小于λP时，才可以应用欧拉公式计算临界力或临界应力。这类压杆称为大柔度杆或细长杆，欧拉公式只适用于大柔度杆。
由于欧拉公式是假设材料在线弹性范围内的条件下，根据挠曲线近似微分方程导出的，而应用此微分方程时，材料必须适用胡克定律。当压杆的临界应力σcr超过材料的比例极限时，胡克定律不再适用，欧拉公式也就不适用了。故欧拉公式的适用范围是：临界应力σcr不超过材料的比例极限。即
有
若设λP为压杆的临界应力达到材料的比例极限σP时的柔度值，则
故欧拉公式的适用范围为
式（11-13）表明，当压杆的柔度不小于λP时，才可以应用欧拉公式计算临界力或临界应力。这类压杆称为大柔度杆或细长杆，欧拉公式只适用于大柔度杆。从式（11-12）中可知，λP的值取决于材料性质，不同的材料都有自己的E值和σP值，所以不同材料制成的压杆，其λP值不同，欧拉公式的适用范围也不同。
对于用Q235钢制成的压杆，E＝200GPa，σP＝200MPa，其判别柔度λP为
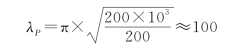
若压杆的柔度λ小于λP，则这类杆称为小柔度杆或非细长杆。小柔度杆的临界应力大于材料的比例极限，这时的压杆将产生塑性变形，称为弹塑性稳定问题。
【例11-2】 图11-8所示的矩形截面压杆，其支承情况为：在平面（纸面平面）内，两端固定；出平面（与纸面垂直的平面）内，下端固定，上端自由。已知l＝3m，b＝0.1m，材料的弹性模量E＝200GPa，比例极限σP＝200MPa，试计算该压杆的临界力。
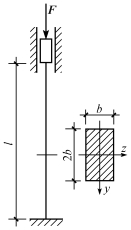
图11-8
【解】 （1）判断失稳方向。由于杆的上端在两个平面（在平面与出平面）内的支承情况不同，因此压杆在两个平面内的长细比也不同，压杆将首先在λ值大的平面内失稳。两种情况下的λ值分别为
平面内：
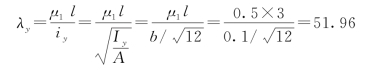
平面外：
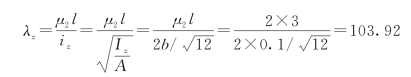
因λz＞λy，所以杆若失稳，将发生在出平面内。
（2）判定该压杆是否可用欧拉公式求临界力。
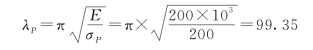
因λz＞λP，故可用欧拉公式求临界力，其值为
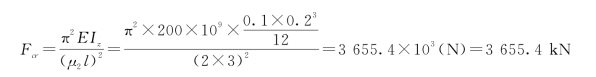
有关建筑力学（第3版）的文章
- 详细阅读
-
建筑力学第3版：轴向拉（压）杆斜截面应力详细阅读
由式（7-6）、式（7-7）可知，轴向拉压杆在斜截面上有正应力和剪应力，它们的大小随截面的方位α角的变化而变化。当α＝0°时，正应力达到最大值：由此可见，拉压杆的最大正应力发生在横截面上。当α＝90°时，σα＝τα＝0，这表明在平行于杆轴线的纵向截面上无任何应力。......
2023-08-26
-
建筑力学第3版-临界应力总图-压杆计算公式详细阅读
如果将压杆的临界应力根据其柔度不同而分别计算的情况用一个简图来表示，该图形就称为压杆的临界应力总图。图11-9与图11-10即某塑性材料的临界应力总图。由临界应力总图可以看出，Q235钢应在λ＝0～123时用抛物线形经验公式计算临界应力，在λ＞123时用欧拉公式计算临界应力。......
2023-08-26
-
欧拉公式：细长压杆临界力计算方法详细阅读
下面介绍不同约束条件下压杆的临界力计算公式。两端铰支细长杆的临界力计算公式——欧拉公式。从欧拉公式可以看出，细长压杆的临界力Fcr与压杆的弯曲刚度成正比，而与杆长l的平方成反比。杆端为其他约束的细长压杆，其临界力计算公式可参考前面的方法导出，也可以采用类比的方法得到。经验表明，具有相同挠曲线形状的压杆，其临界力计算公式也相同。......
2023-06-16
-
建筑力学研究任务和内容，建筑力学第3版详细阅读
建筑力学的任务是研究结构的几何组成规律，以及在荷载作用下结构和构件的强度、刚度和稳定性问题。具体来说，建筑力学将讨论下列几个方面的内容：力系的简化和力系平衡问题。......
2023-08-26
-
建筑力学（第3版）中荷载作用下位移计算的通用详细阅读
利用虚功原理推导结构在荷载作用下位移计算的一般公式，首先要确定力状态和位移状态。利用式计算结构位移时，应根据结构的具体情况，只考虑其中一项或两项。这种用虚设单位荷载产生的内力，在实际状态荷载所引起的位移上做虚功，而利用虚功原理计算结构位移的方法，称为单位荷载法。单位荷载法计算位移公式适用于弹性材料和非弹性材料，可以用于计算静定结构的位移，也可以用于计算超静定结构的位移。......
2023-08-26
-
压杆柔度与临界应力的欧拉公式计算方法详细阅读
于是临界应力可写为令则上式为计算压杆临界应力的欧拉公式，式中λ称为压杆的柔度。从式（9-3）还可以看出，压杆的柔度值越大，则其临界应力越小，压杆就越容易失稳。因此，欧拉公式的适用范围应当是压杆的临界应力σcr不超过材料的比例极限σP，即有若设λP为压杆的临界应力达到材料的比例极限σP时的柔度值，则故欧拉公式的适用范围为上式表明，当压杆的柔度不小于λP时，才可以应用欧拉公式计算临界力或临界应力。......
2023-06-16
-
大力士马迪夫与欧拉公式：趣味物理学续篇详细阅读
凡尔纳描写过一个叫马迪夫的大力士：“他的脑袋硕大无比，身材高大挺拔，胸膛像铁匠的风囊一样壮，腿和木头柱子差不多粗，胳膊像起重机，拳头就像是个铁锤……”凡尔纳对大力士马迪夫这一壮举的描述如下：已经把支撑船身的物体移走了，船随时都可以下水。一位大力士用手抓住“特拉波克罗”号船身上的缆索，身子几乎贴在了地面上。快艇被大力士拯救了！这位了不起的大英雄，就是马迪夫。......
2023-11-18
相关推荐