如果将压杆的临界应力根据其柔度不同而分别计算的情况用一个简图来表示，该图形就称为压杆的临界应力总图。图11-9与图11-10即某塑性材料的临界应力总图。由临界应力总图可以看出，Q235钢应在λ＝0～123时用抛物线形经验公式计算临界应力，在λ＞123时用欧拉公式计算临界应力。......
2023-08-26
《建筑力学第3版》-细长压杆临界力计算
【摘要】：以上讨论的是两端铰支的细长压杆的临界力计算。对于其他支承形式的压杆，也可用同样方法导出其临界力的计算公式。因此，可将两端铰支约束压杆的挠曲线形状取为基本情况，而将其他杆端约束条件下压杆的挠曲线形状与之进行对比，从而得到相应杆端约束条件下压杆临界力的计算公式。表11-1各种支承约束条件下等截面压杆临界力的欧拉公式以上讨论的都是理想的支承情况。现分别计算两种截面杆的临界力。
以上讨论的是两端铰支的细长压杆的临界力计算。对于其他支承形式的压杆，也可用同样方法导出其临界力的计算公式。经验表明，具有相同挠曲线形状的压杆，其临界力计算公式也相同。因此，可将两端铰支约束压杆的挠曲线形状取为基本情况，而将其他杆端约束条件下压杆的挠曲线形状与之进行对比，从而得到相应杆端约束条件下压杆临界力的计算公式。为此，可将欧拉公式写成统一的形式，即
式中 E——材料的弹性模量；
I——压杆横截面对形心轴的与μ对应的最小惯性矩；
μ——长度系数，它反映了不同杆端约束对临界力的影响，其值可按表11-1确定；
l——压杆长度；
μl——压杆计算长度。
表11-1 各种支承约束条件下等截面压杆临界力的欧拉公式
以上讨论的都是理想的支承情况。工程中压杆的实际支承情况比较复杂，有时很难简单地将其归结为哪一种理想情况，需要做具体分析。下面通过几个实例来说明杆端支承情况的简化。
（1）柱形铰支承。图11-5所示的连杆，两端为柱形铰支承。若连杆在较大刚度平面（水平面xy平面）内弯曲时，两端可简化为铰支，如图11-5（a）所示；若在较小刚度平面（铅垂面xz平面）内弯曲时，如图11-5（b）所示，则应根据两端的实际固结程度而定。如接头的刚性较好，使其不能转动，就可简化为固定端；如果有可能发生微小转动，则应简化为铰支，这样处理比较安全。
（2）焊接或铆接。对于杆端与支承处焊接或铆接的压杆，如图11-6所示，桁架的AC杆受力后，两端连接处仍可能产生微小转动，故不能认为是固定端，而应按铰支端考虑。
（3）固定端。例如，与坚实基础固结成一体的柱脚可简化为固定端。
总之，理想的固定端和铰支端是不多见的，实际杆端的支承情况往往介于固定端和铰支端之间。一般来说，只要杆端截面稍有转动的可能，就不应当作理想的固定端处理。
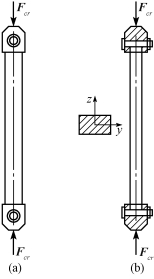
图11-5
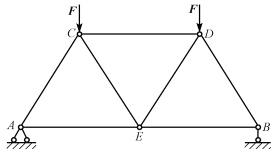
图11-6
【例11-1】 图11-7所示细长压杆的两端为球形铰，弹性模量E＝200GPa，截面形状为：（1）圆形截面，d＝5cm；（2）16号工字钢。杆长均为l＝2m，试用欧拉公式计算其临界荷载。
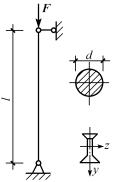
图11-7
【解】 因压杆两端为球形铰，故μ＝1。现分别计算两种截面杆的临界力。
（1）圆形截面杆：
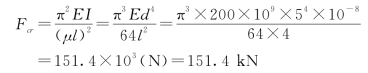
（2）I形截面杆：
对压杆为球形铰支承的情况，应取I＝Imin＝Iy。由型钢表查得
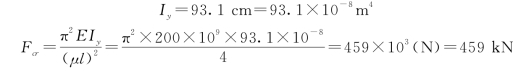
有关建筑力学（第3版）的文章
- 详细阅读
-
欧拉公式：细长压杆临界力计算方法详细阅读
下面介绍不同约束条件下压杆的临界力计算公式。两端铰支细长杆的临界力计算公式——欧拉公式。从欧拉公式可以看出，细长压杆的临界力Fcr与压杆的弯曲刚度成正比，而与杆长l的平方成反比。杆端为其他约束的细长压杆，其临界力计算公式可参考前面的方法导出，也可以采用类比的方法得到。经验表明，具有相同挠曲线形状的压杆，其临界力计算公式也相同。......
2023-06-16
-
建筑力学第3版：轴向拉（压）杆斜截面应力详细阅读
由式（7-6）、式（7-7）可知，轴向拉压杆在斜截面上有正应力和剪应力，它们的大小随截面的方位α角的变化而变化。当α＝0°时，正应力达到最大值：由此可见，拉压杆的最大正应力发生在横截面上。当α＝90°时，σα＝τα＝0，这表明在平行于杆轴线的纵向截面上无任何应力。......
2023-08-26
-
压杆稳定条件的应用与建筑力学（第3版）相关详细阅读
即已知压杆的几何尺寸、所用材料及支承条件，按稳定条件计算其能够承受的许用荷载值F。在稳定条件式中，已知φ后才能标出A值，但在杆件尺寸未确定之前，无法确定λ值，因而也就无法确定φ值，故可采用试算的方法。然后，根据截面尺寸及杆长计算出柔度λ，由λ查出φ，再以算得的面积A和查得的φ值验算其是否满足稳定条件。......
2023-08-26
-
如何计算钢结构中的压杆力？详细阅读
9-1 如图9-11 所示正方形桁架，各杆各截面的弯曲刚度均为EI，且均为细长杆。9-2 如图9-12 所示两端球形铰支细长压杆，弹性模量E=200 GPa。图9-13题9-39-4 如图9-14 所示矩形截面压杆，有三种支持方式。其他各项条件相同，只须计算各压杆的相当长度。图9-14题9-4图图9-15题9-5图9-6 如图9-16 所示托架，实心圆截面杆BD 的直径为d=32 mm，长度l=1 m，两端可视为球铰，材料为Q235，E=200 GPa，σS=240 MPa，λP=100，λS=60，临界应力经验公式为σcr=a-bλ，其中a=310 MPa，b=1.14 MPa。......
2023-06-19
-
轴向拉（压）杆横截面上的应力|建筑力学（第3详细阅读
由此可得，横截面上各点处的正应力σ大小相等[图7-7]。若杆的轴力为N，横截面面积为A，则正应力为应力的单位为帕斯卡（简称帕），1帕＝1牛顿/平方米，或表示为1Pa＝1N/m2。由于前面已规定了轴力的正负号，由式（7-1）可知，正应力也随轴力N而有正负之分，即拉应力为正，压应力为负。直杆的横截面面积A＝10cm2，试计算各段横截面上的正应力。图7-8用截面法求出各段轴力：由式（7-1）计算各段的正应力值为......
2023-08-26
-
建筑力学第3版：压杆平衡与不稳定平衡的分析详细阅读
图11-1上述现象表明，在轴向压力F由小逐渐增大的过程中，压杆由稳定的平衡转变为不稳定的平衡，这种现象称为压杆丧失稳定性或者压杆失稳。显然压杆是否失稳取决于轴向压力的数值，压杆由直线状态的稳定的平衡过渡到不稳定的平衡时所对应的轴向压力，称为压杆的临界压力或临界力，用Fcr表示。......
2023-08-26
-
建筑力学（第3版）：矩形截面杆自由扭转详细阅读
在建筑结构中，矩形截面受扭杆一般都处于约束扭转状态。但是，由于约束扭转所引起的正应力可忽略不计，所以可按自由扭转的情况进行计算。这里直接给出矩形截面扭转轴的弹性力学解释的结论：矩形截面扭转轴的横截面上仍然只有剪应力，虽有正应力，但只要h/b的值不太大，正应力的数值很小，可忽略不计。横截面上的最大剪应力发生在长边的中点处。单位长度扭转角全轴的扭转角......
2023-08-26
相关推荐