弯曲、扭转组合变形的强度计算与前面讨论过的几类组合变形不同。而在弯曲、扭转组合变形时，杆中最容易破坏的危险点处，既存在正应力σ，又存在剪应力τ。弯曲、扭转组合变形的强度条件为或式中σ——杆件危险点处横截面上的正应力；τ——杆件危险点处横截面上的剪应力；[σ]——材料的许用正应力。......
2023-08-26
建筑力学第3版：组合变形的计算方法及应用
【摘要】：当这六种力（或力矩）中只有某一个作用时，杆件就会产生基本变形。图10-1杆件同时有两种或两种以上的基本变形的组合时，称为组合变形。图10-2对发生组合变形的杆件计算应力和变形时，可先将荷载进行简化或分解，使简化或分解后的静力等效荷载，各自只引起一种简单变形，分别计算，再进行叠加，就得到原来的荷载引起的组合变形时应力和变形。当然，必须满足小变形假设及力与位移之间呈线性关系这两个条件才能应用叠加原理。
在实际工程中，杆件的受力是很复杂的，除拉伸（压缩）、剪切、扭转和弯曲外，还有如图10-1所示的一端固定、另一端自由的悬臂杆。若在其自由端截面上作用有一空间任意的力系，总可以将空间的任意力系沿截面形心主惯性轴xOyz简化，得到向x、y、z三坐标轴上投影Px、Py、Pz和对x、y、z三坐标轴的力矩Mx、My、Mz。当这六种力（或力矩）中只有某一个作用时，杆件就会产生基本变形。
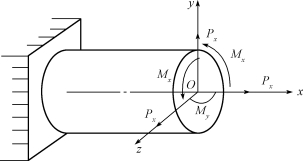
图10-1
杆件同时有两种或两种以上的基本变形的组合时，称为组合变形。图10-2（a）所示的屋架檩条，将产生相互垂直的两个平面弯曲的组合变形；图10-2（b）所示的钻床立柱，将产生轴向拉伸与平面弯曲的组合变形；图10-2（c）所示的机床传动轴，将产生扭转与两相互垂直平面内平面弯曲的组合变形。其他如卷扬机的机轴，同时承受扭转和弯曲的作用，楼梯的斜梁、烟囱、挡土墙等构件都同时承受压缩和平面弯曲的共同作用。
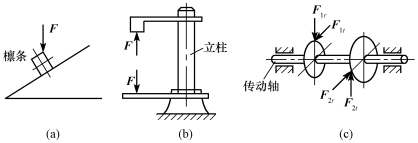
图10-2
对发生组合变形的杆件计算应力和变形时，可先将荷载进行简化或分解，使简化或分解后的静力等效荷载，各自只引起一种简单变形，分别计算，再进行叠加，就得到原来的荷载引起的组合变形时应力和变形。当然，必须满足小变形假设及力与位移之间呈线性关系这两个条件才能应用叠加原理。
有关建筑力学（第3版）的文章
- 详细阅读
-
建筑力学第3版：轴向拉伸与弯曲组合变形的强度详细阅读
下面结合图10-7所示的受力杆件，说明拉（压）、弯组合变形时的正应力及其强度计算。图10-6图10-7计算杆件在拉（压）、弯组合变形下的正应力时，与斜弯曲类似，仍采用叠加的方法，即分别计算杆件在轴向拉伸（压缩）和弯曲变形下的应力，再代数相加。用式计算正应力时，应注意正、负号：轴向拉伸时，σ′为正；压缩时，σ′为负。最大拉应力为最大压应力为......
2023-08-26
-
建筑力学第3版：刚体与变形固体及基本假设详细阅读
忽略了物体微小的变形后便可将物体看成刚体。一般情况下，物体受力后，既有弹性变形，又有塑性变形。材料力学的研究对象是由连续、均匀、各向同性的变形固体材料制成的构件，且限于小变形范围。按照连续、均匀、各向同性假设而理想化了的一般变形固体称为理想变形固体。......
2023-08-26
-
《建筑力学（第3版）》-叠加法求梁变形详细阅读
在小变形条件下，当梁内的应力不超过材料的比例极限时，梁的挠曲线近似微分方程是一个线性微分方程，因此可用叠加法求梁的变形，即梁在几个简单荷载共同作用下某截面的挠度和转角等于各个简单荷载单独作用时该截面挠度或转角的代数和。表9-2梁在简单荷载作用下的挠度和转角续表试用叠加法计算图9-38所示简支梁的跨中挠度yC及A截面的转角θA。......
2023-08-26
-
建筑力学第3版：圆杆扭转变形和刚度条件详细阅读
GIP称为杆件的抗扭刚度，它反映杆件抵抗扭转变形的能力。由得按刚度条件确定d。要使轴同时满足强度和刚度条件，需取轴的直径d＝52mm。......
2023-08-26
-
建筑力学第3版：相对变形、泊松比的测定方法详细阅读
绝对变形的大小只反映杆的总变形量，而无法说明杆的变形程度。因此，为了度量杆的变形程度，还需计算单位长度内的变形量。对于轴力为常量的等截面直杆，其变形处处相等。试验表明，当拉（压）杆内应力不超过某一限度时，横向线应变ε′与纵向线应变ε之比的绝对值为一常数，即μ称为横向变形因数或泊松比，是无因次的量，其数值随材料而异，也是通过试验测定的。......
2023-08-26
-
建筑力学（第3版）：变形体虚功原理详细阅读
（二）变形体的虚功原理前面所讲到的简支梁，在力P1作用下会引起内力，那么，内力在其本身引起的变形上所做的功，称为内力实功，用表示；P1所做的功W11称为外力实功。计算结构位移时，需要用到的是虚力原理，不过习惯上仍称它为虚功原理，以下仍沿用这一称呼。......
2023-08-26
-
建筑力学第3版-悬臂梁弯矩图计算方法详细阅读
图14-15所示的在集中力及均布荷载作用下悬臂梁的弯矩图，其形状虽与图14-14相似，但不能采用其面积和形心位置公式，因为B处的剪力不为零。这时应采用图形叠加的方法解决。存在以下几种具体情况：1）如果在两个图形都是直线，则标距yC可取自其中任一图形。2）如果在两个图形中，一个是曲线，一个是直线，曲线图形只能取面积，直线图形取yC。......
2023-08-26
相关推荐