在小变形条件下，梁的内力、支座反力、应力和变形等参数均与荷载呈线性关系，每一荷载单独作用时引起的某一参数不受其他荷载的影响。为了便于应用叠加法绘制内力图，表9-1中给出了梁在简单荷载作用下的弯矩图，可供查用。由上例可以看出，用分段叠加法作外伸梁的弯矩图时，不需要求支座反力，就可以画出其弯矩图。......
2023-08-26
《建筑力学（第3版）》-叠加法求梁变形
【摘要】：在小变形条件下，当梁内的应力不超过材料的比例极限时，梁的挠曲线近似微分方程是一个线性微分方程，因此可用叠加法求梁的变形，即梁在几个简单荷载共同作用下某截面的挠度和转角等于各个简单荷载单独作用时该截面挠度或转角的代数和。表9-2梁在简单荷载作用下的挠度和转角续表试用叠加法计算图9-38所示简支梁的跨中挠度yC及A截面的转角θA。
在小变形条件下，当梁内的应力不超过材料的比例极限时，梁的挠曲线近似微分方程是一个线性微分方程，因此可用叠加法求梁的变形，即梁在几个简单荷载共同作用下某截面的挠度和转角等于各个简单荷载单独作用时该截面挠度或转角的代数和。
梁在简单荷载作用下的挠度和转角，可从表9-2中查得。
表9-2 梁在简单荷载作用下的挠度和转角
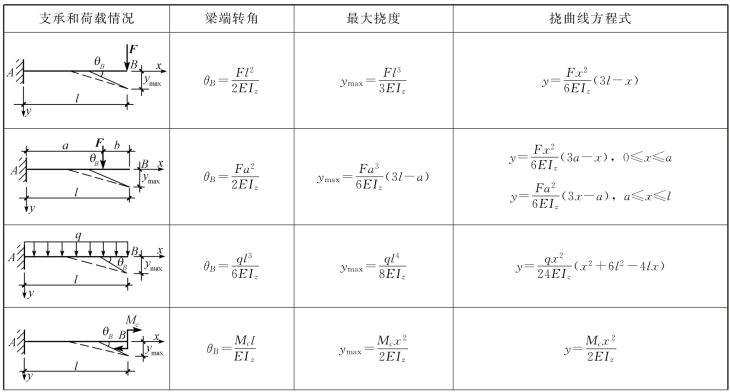
续表
【例9-14】 试用叠加法计算图9-38所示简支梁的跨中挠度yC及A截面的转角θA。
图9-38
【解】 可先分别计算q与F单独作用下的跨中挠度yC1和yC2，由表9-2查得：
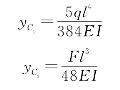
q、F共同作用下的跨中挠度则为
同样，也可求得A截面的转角为
【例9-15】 某外伸梁，受力如图9-39（a）所示，已知梁的抗弯刚度为EI，试用叠加法求C截面的挠度。
图9-39
【解】 表9-2中虽然没有外伸梁的位移计算公式，但经过分析和处理后，此题仍可利用表9-2中的有关公式用叠加法求得。
外伸梁在P作用下的挠曲线如图9-39（a）中的虚线所示，B截面处的挠度等于零，但转角不等于零。在计算C截面的挠度时，可先将梁的BC段看成B端为固定端的悬臂梁[图9-39（b）]，此悬臂梁在P作用下C截面的挠度为yC1。但外伸梁的B截面处并非固定不动，而要产生转角θB，B截面的转动对BC段梁的影响，相当于使BC段绕B点刚性转动，此时C截面的竖向位移用yC2表示[图9-39（c）]。因θB很小，yC2可用aθB表示。将图9-39（b）中的yC1与图9-39（c）中的yC2相叠加，就是外伸梁C截面的挠度yC，即
由表9-2查得：
这样，如能求出θB，便可求得yC2，从而进一步求得yC。
θB是图9-39（a）所示外伸梁在P作用下B截面的转角。求θB时，可用图9-39（d）所示的等效力系，即将外力P平移到B点并附加一力矩M＝Pa，通过图9-39（d）所示简图求出的B截面的转角，就是图9-39（a）所示外伸梁B截面的转角。在图9-39（d）中，集中力P作用在梁的支座上，它不引起梁的变形，仅M使梁变形。简支梁在M作用下B截面的转角[图9-39（e）]可从表9-2中查得：
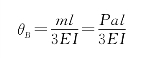
所以
外伸梁C截面的挠度为
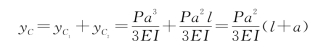
有关建筑力学（第3版）的文章
- 详细阅读
-
荷载位置固定求量值-建筑力学第3版详细阅读
，yn，则在这组集中荷载共同作用下，量值S为应用式时，需注意竖标yi的正、负号。式表明，均布荷载引起的量值等于荷载集度乘以荷载作用段对应的影响线面积。......
2023-08-26
-
截面法求内力-建筑力学（第3版）详细阅读
图9-4求内力仍采用截面法。力Q和力偶矩M就是梁弯曲时横截面上产生的两种不同形式的内力，力Q称为剪力，力偶矩M称为弯矩。简支梁受载如图9-7所示，试用截面法求截面1—1上的内力。......
2023-08-26
-
建筑力学第3版：圆杆扭转变形和刚度条件详细阅读
GIP称为杆件的抗扭刚度，它反映杆件抵抗扭转变形的能力。由得按刚度条件确定d。要使轴同时满足强度和刚度条件，需取轴的直径d＝52mm。......
2023-08-26
-
建筑力学第3版-悬臂梁弯矩图计算方法详细阅读
图14-15所示的在集中力及均布荷载作用下悬臂梁的弯矩图，其形状虽与图14-14相似，但不能采用其面积和形心位置公式，因为B处的剪力不为零。这时应采用图形叠加的方法解决。存在以下几种具体情况：1）如果在两个图形都是直线，则标距yC可取自其中任一图形。2）如果在两个图形中，一个是曲线，一个是直线，曲线图形只能取面积，直线图形取yC。......
2023-08-26
-
建筑力学（第3版）：变形体虚功原理详细阅读
（二）变形体的虚功原理前面所讲到的简支梁，在力P1作用下会引起内力，那么，内力在其本身引起的变形上所做的功，称为内力实功，用表示；P1所做的功W11称为外力实功。计算结构位移时，需要用到的是虚力原理，不过习惯上仍称它为虚功原理，以下仍沿用这一称呼。......
2023-08-26
-
建筑力学第3版：组合变形的计算方法及应用详细阅读
当这六种力（或力矩）中只有某一个作用时，杆件就会产生基本变形。图10-1杆件同时有两种或两种以上的基本变形的组合时，称为组合变形。图10-2对发生组合变形的杆件计算应力和变形时，可先将荷载进行简化或分解，使简化或分解后的静力等效荷载，各自只引起一种简单变形，分别计算，再进行叠加，就得到原来的荷载引起的组合变形时应力和变形。当然，必须满足小变形假设及力与位移之间呈线性关系这两个条件才能应用叠加原理。......
2023-08-26
-
建筑力学第3版：刚体与变形固体及基本假设详细阅读
忽略了物体微小的变形后便可将物体看成刚体。一般情况下，物体受力后，既有弹性变形，又有塑性变形。材料力学的研究对象是由连续、均匀、各向同性的变形固体材料制成的构件，且限于小变形范围。按照连续、均匀、各向同性假设而理想化了的一般变形固体称为理想变形固体。......
2023-08-26
相关推荐