横截面上各点均无剪应变，故纯弯曲时，横截面上无剪应力。当弯矩为正时，梁下部纤维伸长，故产生拉应力；上部纤维缩短而产生压应力。进一步的研究表明，剪力的存在对正应力分布规律的影响很小。计算C截面上K点的正应力。在已知梁的横截面形状和尺寸、材料及所受荷载的情况下，可校核梁是否满足正应力强度条件，即校核是否满足式（9-9）。弯曲正应力强度条件。......
2023-08-26
建筑力学第3版：弯曲剪应力强度计算
【摘要】：在梁的强度计算中，必须同时满足正应力和剪应力两个强度条件。在选择梁的截面时，通常是先按正应力强度条件选择截面尺寸，然后再进行剪应力强度校核。对于某些特殊情况，梁的剪应力强度条件也可能起到控制作用。例如，梁的跨度很小，或在支座附近有较大的集中力作用，这时梁可能出现弯矩较小，而剪力却很大的情况，这就必须注意剪应力强度条件是否满足。校核正应力强度及剪应力强度。
在工程中，大多数梁是在横向力作用下发生弯曲，横截面上的内力不仅有弯矩，而且还有剪力。因此，横截面上除具有正应力外，还具有剪应力。
一般情况下，梁的弯曲正应力是梁强度计算的主要依据，但在某些特殊情况下，如梁的跨度较小（短粗梁）或截面高而窄（薄壁梁），弯矩较小而剪力较大的梁，其剪应力可能达到相当大的数值，就要求进行剪应力的强度计算。下面研究等直截面梁上的剪应力。
1.矩形截面梁的剪应力
对于高度h大于宽度b的矩形截面梁，其横截面上的剪力Q沿y轴方向，如图9-26（a）所示，现假设剪应力的分布规律如下：
（1）横截面上各点处的剪应力τ都与剪力Q方向一致；
（2）横截面上距中性轴等距离各点处剪应力大小相等，即沿截面宽度为均匀分布。
根据以上假设，可以推导出矩形截面梁横截面上任意一点处剪应力的计算公式为
式中 Q——横截面上的剪力；
Iz——横截面对中性轴的惯性矩；
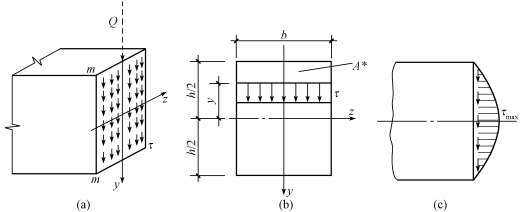
图9-26
b——横截面的宽度；
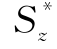——所求应力点的水平线到截面下（或上）边缘之间的面积A*对z轴的静矩。
如图9-26（b）所示的截面，y0是面积为A*的材料的形心纵坐标，则面积为A*的材料对z轴的静矩为
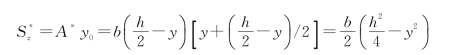
将上式及Iz＝bh3/12代入式（9-12），得：
式（9-13）表明，剪应力沿截面高度按二次抛物线规律变化[图9-26（c）]。在截面的上、下边缘
处的剪应力为零；在中性轴处（y＝0）的剪应力最大，其值为
即矩形截面上的最大剪应力为截面上平均剪应力（Q/A）的1.5倍，发生在中性轴上。
【例9-11】 一矩形截面简支梁如图9-27所示。已知l＝3m，h＝160mm，b＝100mm，h1＝40mm，P＝3kN，求截面m—m上K点的剪应力。
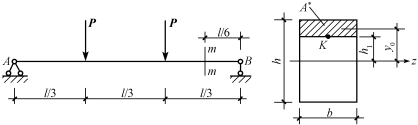
图9-27
【解】 （1）求支座反力及截面m—m上的剪力。
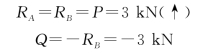
（2）计算截面的惯性矩及面积A*对中性轴的静矩分别为
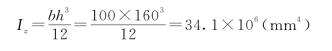
（3）计算截面m—m上K点的剪应力。
【例9-12】 矩形截面梁（b×h）受均布荷载q作用，如图9-28（a）所示，试求σmax和τmax，并比较。
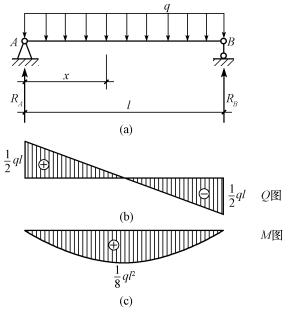
图9-28
【解】 作剪力图和弯矩图，如图9-28（b）、（c）所示。
则梁的最大正应力和最大剪应力分别为
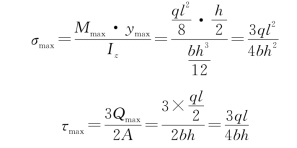
两者比值为
2.I形及T形截面梁的剪应力
I形截面梁由上、下翼缘和腹板组成，如图9-29（a）所示。由于腹板为狭长矩形，仍可采用与矩形截面梁相同的假设。经过与矩形截面梁类似的推导，可得腹板上距中性轴y处点的剪应力为
式中 Iz——整个I形截面对中性轴的惯性矩；
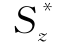——横截面上所求剪应力处的水平线以下（或以上）至边缘部分面积A*对中性轴的静矩；
d——腹板的厚度。
剪应力沿腹板高度的分布，仍按抛物线分布，如图9-29（a）所示，最大剪应力τmax仍在截面的中性轴上。至于翼缘上的剪应力，其值则远小于腹板上的剪应力，在计算时可以不考虑，如图9-29（b）、（c）所示。
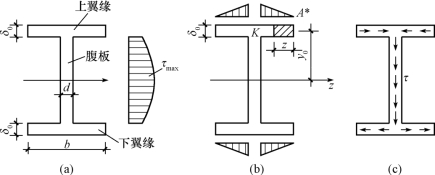
图9-29
T形截面也是工程中常用的截面形式，它是由两个矩形截面组成[图9-30（a）]。下面的狭长矩形与I形截面的腹板类似，这部分的剪应力仍用式（9-15）计算。剪应力的分布仍按抛物线规律变化，最大剪应力仍发生在中性轴上，如图9-30（b）所示。
3.圆形和圆环形截面梁的剪应力
圆形和圆环形截面的最大剪应力均发生在中性轴上，并沿中性轴均匀分布，如图9-31所示。其值分别为
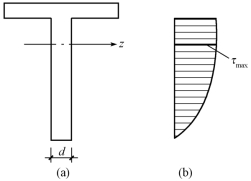
图9-30
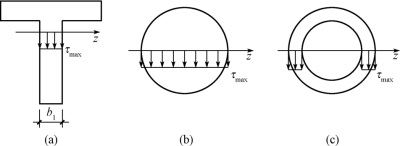
图9-31
圆形截面
薄壁圆环形截面
另外，对箱形截面梁和T形截面梁都可采用式（9-15）计算其腹板上的剪应力，最大剪应力仍发生在截面的中性轴上。
4.梁的剪应力强度条件
为保证梁的剪应力强度，梁的最大剪应力不应超过材料的许用剪应力[τ]，即
式（9-16）称为梁的剪应力强度条件。
在梁的强度计算中，必须同时满足正应力和剪应力两个强度条件。但在一般情况下，正应力强度条件往往起主导作用。在选择梁的截面时，通常是先按正应力强度条件选择截面尺寸，然后再进行剪应力强度校核。对于细长梁，按正应力强度条件设计的梁一般都能满足剪应力强度要求，就不必做剪应力校核。对于某些特殊情况，梁的剪应力强度条件也可能起到控制作用。例如，梁的跨度很小，或在支座附近有较大的集中力作用，这时梁可能出现弯矩较小，而剪力却很大的情况，这就必须注意剪应力强度条件是否满足。又如，对组合工字钢梁，其腹板上的剪应力可能较大；对木梁，在木材顺纹方向的抗剪能力很差。这些情况都应注意，在进行正应力强度校核的同时，还要进行剪应力的强度校核。
【例9-13】 一外伸工字型钢梁，工字钢的型号为22a，梁上荷载如图9-32（a）所示。已知l＝6m，p＝30kN，q＝6kN/m，[σ]＝170MPa，[τ]＝100MPa，检查此梁是否安全。
【解】 （1）绘剪力图、弯矩图，如图9-32（b）、（c）所示。
（2）由型钢表查得有关数据。
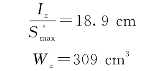
（3）校核正应力强度及剪应力强度。
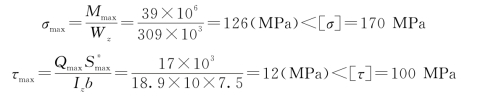
所以，梁是安全的。
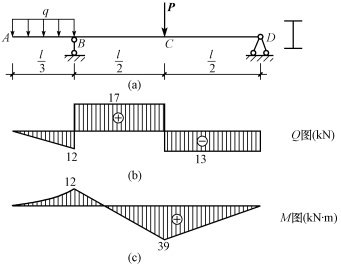
图9-32
有关建筑力学（第3版）的文章
- 详细阅读
-
建筑力学第3版：斜弯曲变形的应力与强度计算详细阅读
图10-3斜弯曲是两个平面弯曲的组合变形，这里将讨论斜弯曲时的正应力和正应力强度计算。也就是说，计算弯曲时的正应力，是将斜弯曲分解为两个平面弯曲，分别计算每个平面弯曲下的正应力，再进行叠加。将荷载F沿截面两对称轴方向分解为Fy和Fz，它们引起的跨中截面上的弯矩分别为梁中的最大正应力为满足正应力强度条件。......
2023-08-26
-
建筑力学（第3版）：弯曲与扭转组合变形强度计详细阅读
弯曲、扭转组合变形的强度计算与前面讨论过的几类组合变形不同。而在弯曲、扭转组合变形时，杆中最容易破坏的危险点处，既存在正应力σ，又存在剪应力τ。弯曲、扭转组合变形的强度条件为或式中σ——杆件危险点处横截面上的正应力；τ——杆件危险点处横截面上的剪应力；[σ]——材料的许用正应力。......
2023-08-26
-
建筑力学第3版：轴向拉伸与弯曲组合变形的强度详细阅读
下面结合图10-7所示的受力杆件，说明拉（压）、弯组合变形时的正应力及其强度计算。图10-6图10-7计算杆件在拉（压）、弯组合变形下的正应力时，与斜弯曲类似，仍采用叠加的方法，即分别计算杆件在轴向拉伸（压缩）和弯曲变形下的应力，再代数相加。用式计算正应力时，应注意正、负号：轴向拉伸时，σ′为正；压缩时，σ′为负。最大拉应力为最大压应力为......
2023-08-26
-
建筑力学（第3版）：挤压计算及强度条件详细阅读
所以，也采用实用计算法，假定在挤压面上的挤压应力σc是均匀分布的，因此式中Pc——挤压面上的挤压力，Pc＝P；Ac——挤压面的计算面积，Ac＝d·t。这样得到的平均挤压应力又称作名义挤压应力。为了防止挤压破坏，挤压面上的挤压应力不得超过连接件材料的许用挤压应力[σc]，即要求图8-5式（8-4）称为挤压强度条件。......
2023-08-26
-
《建筑力学（第3版）》强度条件及校核详细阅读
根据以上分析，为了保证拉（压）杆在工作时不致因强度不够而破坏，杆内的最大工作应力σmax不得超过材料的许用应力[σ]，即式即拉（压）杆的强度条件。已知荷载、构件尺寸及材料的许用应力，根据强度条件校核是否满足强度要求。已知构件的横截面面积及材料的许用应力，根据强度条件可以确定杆能承受的最大轴力，即从而即可求出承载力。......
2023-08-26
-
偏心拉伸的强度计算与截面核心|建筑力学（第3详细阅读
偏心拉伸（压缩）是相对于轴向拉伸（压缩）而言的。单向偏心拉伸（压缩）时，杆件横截面上最大正应力的位置很容易判断。所以，双向偏心拉伸（压缩）实际上是轴向拉伸（压缩）与两个平面弯曲的组合变形。这就要求将偏心压力控制在某一区域范围内，从而使截面上只有压应力而无拉应力。这一范围即截面核心。......
2023-08-26
-
圆轴扭转剪应力分布-《建筑力学（第3版）》详细阅读
为解决圆轴扭转的强度问题，在求得横截面上的扭矩之后，还要进一步研究横截面上的应力。在整个横截面上，所有这些微力矩之和应等于该截面的扭矩T，因此将式代入得积分即为横截面的极惯性矩，因而式可改写为将式代入式得这就是圆轴扭转时横截面上的剪应力计算公式。式中，T为横截面上的扭矩；IP为圆截面对圆心的极惯性矩；ρ为所求应力点至圆心的距离。因这里的剪应力正、负无实用意义，一般只计算其绝对值。......
2023-08-26
相关推荐