GIP称为杆件的抗扭刚度，它反映杆件抵抗扭转变形的能力。由得按刚度条件确定d。要使轴同时满足强度和刚度条件，需取轴的直径d＝52mm。......
2023-08-26
建筑力学（第3版）：矩形截面杆自由扭转
【摘要】：在建筑结构中，矩形截面受扭杆一般都处于约束扭转状态。但是，由于约束扭转所引起的正应力可忽略不计，所以可按自由扭转的情况进行计算。这里直接给出矩形截面扭转轴的弹性力学解释的结论：矩形截面扭转轴的横截面上仍然只有剪应力，虽有正应力，但只要h/b的值不太大，正应力的数值很小，可忽略不计。横截面上的最大剪应力发生在长边的中点处。单位长度扭转角全轴的扭转角
在建筑结构中，矩形截面受扭杆一般都处于约束扭转状态。但是，由于约束扭转所引起的正应力可忽略不计，所以可按自由扭转的情况进行计算。这里直接给出矩形截面扭转轴的弹性力学解释的结论：
（1）矩形截面扭转轴的横截面上仍然只有剪应力，虽有正应力，但只要h/b的值不太大，正应力的数值很小，可忽略不计。
（2）截面周边上各点处的剪应力的方向与周边平行（相切），并形成与截面上扭矩相同转向的剪应力流，如图8-23（c）所示，剪应力的大小均呈非线性变化，中点处的剪应力最大。
（3）截面两条对称轴上各点处剪应力的方向都垂直于对称轴，其他线上各点的剪应力则是程度不同的倾斜。
（4）截面中心和四个角点处的剪应力等于零。
（5）横截面上的最大剪应力发生在长边的中点处。其计算公式为
式中 Wt——相当抗扭截面模量；
h——矩形截面长边的长度；
b——矩形截面短边的长度；
T——截面上的扭矩；
β——与截面尺寸的比值h/b有关的系数，可由表8-1查得。
短边中点处的剪应力也相当大，其计算公式为
式中 γ——与截面尺寸的比值h/b有关的系数，可由表8-1查得。
单位长度扭转角θ为
式中 α——与截面尺寸的比值h/b有关的系数，可由表8-1查得；
G——材料的剪切弹性模量。
表8-1 矩形截面杆纯扭转时的系数α、β和γ
【例8-6】 矩形截面杆的尺寸及荷载如图8-24所示，材料的剪切弹性模量G＝0.55×103MPa，求：（1）横截面最大剪应力；（2）短边中点处的剪应力；（3）扭转角。
图8-24
【解】 （1）轴内各横截面的扭矩相等，T＝100N·m。
由
＝1.375，查表8-1（插值法）得
因各横截面的剪应力分布相同，最大剪应力发生在长边中点。
（2）短边中点处的剪应力。
（3）扭转角。
单位长度扭转角
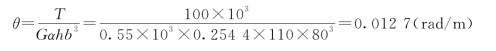
全轴的扭转角
有关建筑力学（第3版）的文章
- 详细阅读
-
建筑力学第3版：轴向拉（压）杆斜截面应力详细阅读
由式（7-6）、式（7-7）可知，轴向拉压杆在斜截面上有正应力和剪应力，它们的大小随截面的方位α角的变化而变化。当α＝0°时，正应力达到最大值：由此可见，拉压杆的最大正应力发生在横截面上。当α＝90°时，σα＝τα＝0，这表明在平行于杆轴线的纵向截面上无任何应力。......
2023-08-26
-
建筑力学第3版：等截面直杆转角位移方程详细阅读
图15-30根据叠加原理，其杆端弯矩可分为图15-30、、、四种情况叠加，查表15-1得到：由A端转角θA引起的杆端力为由B端转角θB引起的杆端力为由两端相对侧移Δ引起的杆端力为如果有荷载作用，其固端弯矩、固端剪力为，根据叠加原理，将以上所得叠加有式就是两端固定的等截面单跨超静定梁的转角位移方程。可以将杆件分为图15-31、、三种情况叠加，查表15-1，同样方法可得图15-31式为一端固定，另一端铰支的等截面单跨超静定梁的转角位移方程。......
2023-08-26
-
轴向拉（压）杆横截面上的应力|建筑力学（第3详细阅读
由此可得，横截面上各点处的正应力σ大小相等[图7-7]。若杆的轴力为N，横截面面积为A，则正应力为应力的单位为帕斯卡（简称帕），1帕＝1牛顿/平方米，或表示为1Pa＝1N/m2。由于前面已规定了轴力的正负号，由式（7-1）可知，正应力也随轴力N而有正负之分，即拉应力为正，压应力为负。直杆的横截面面积A＝10cm2，试计算各段横截面上的正应力。图7-8用截面法求出各段轴力：由式（7-1）计算各段的正应力值为......
2023-08-26
-
建筑力学第3版：选择合理截面形状详细阅读
从弯曲强度方面考虑，最合理的截面形状是用最少的材料获得最大的抗弯截面模量。梁的强度一般由横截面上的最大正应力控制。当弯矩一定时，横截面上的最大正应力σmax与抗弯截面模量Wz成反比，Wz越大就越有利。而Wz的大小与截面的面积及形状有关，合理的截面形状是指在截面面积A相同的条件下，有较大的抗弯截面模量Wz。所以，I形、槽形截面比矩形截面合理，矩形截面立放比平放合理，正方形截面比圆形截面合理。......
2023-08-26
-
截面法求内力-建筑力学（第3版）详细阅读
图9-4求内力仍采用截面法。力Q和力偶矩M就是梁弯曲时横截面上产生的两种不同形式的内力，力Q称为剪力，力偶矩M称为弯矩。简支梁受载如图9-7所示，试用截面法求截面1—1上的内力。......
2023-08-26
-
圆轴扭转内力扭矩-建筑力学（第3版）详细阅读
在对圆轴进行强度计算之前先要计算出圆轴横截面上的内力——扭矩。根据平衡条件可知，C截面上必存在一个内力偶矩T，与外力偶矩m使左半部保持平衡。此内力偶矩称为扭矩，用T表示。扭矩的单位与力矩相同，常用N·m或kN·m。图8-12与计算轴力的方法类似，用截面法计算扭矩时，通常假定扭矩为正。用截面法分别求出各段上的扭矩。......
2023-08-26
-
圆轴扭转剪应力分布-《建筑力学（第3版）》详细阅读
为解决圆轴扭转的强度问题，在求得横截面上的扭矩之后，还要进一步研究横截面上的应力。在整个横截面上，所有这些微力矩之和应等于该截面的扭矩T，因此将式代入得积分即为横截面的极惯性矩，因而式可改写为将式代入式得这就是圆轴扭转时横截面上的剪应力计算公式。式中，T为横截面上的扭矩；IP为圆截面对圆心的极惯性矩；ρ为所求应力点至圆心的距离。因这里的剪应力正、负无实用意义，一般只计算其绝对值。......
2023-08-26
相关推荐