在对圆轴进行强度计算之前先要计算出圆轴横截面上的内力——扭矩。根据平衡条件可知，C截面上必存在一个内力偶矩T，与外力偶矩m使左半部保持平衡。此内力偶矩称为扭矩，用T表示。扭矩的单位与力矩相同，常用N·m或kN·m。图8-12与计算轴力的方法类似，用截面法计算扭矩时，通常假定扭矩为正。用截面法分别求出各段上的扭矩。......
2023-08-26
圆轴扭转剪应力分布-《建筑力学（第3版）》
【摘要】：为解决圆轴扭转的强度问题，在求得横截面上的扭矩之后，还要进一步研究横截面上的应力。在整个横截面上，所有这些微力矩之和应等于该截面的扭矩T，因此将式代入得积分即为横截面的极惯性矩，因而式可改写为将式代入式得这就是圆轴扭转时横截面上的剪应力计算公式。式中，T为横截面上的扭矩；IP为圆截面对圆心的极惯性矩；ρ为所求应力点至圆心的距离。因这里的剪应力正、负无实用意义，一般只计算其绝对值。
为解决圆轴扭转的强度问题，在求得横截面上的扭矩之后，还要进一步研究横截面上的应力。为此，需从几何变形、物理关系和静力平衡关系三个方面综合研究，以便建立横截面上的应力计算公式。
1.几何方面
从图8-14（a）所示的圆轴中取一微段dx，并从中切取一楔形体O1O2ABCD[图8-14（b）]，则其变形如图8-14（c）所示。圆轴表层的矩形ABCD变为平行四边形ABC′D′；与轴线相距为ρ的矩形abcd变为平行四边形abc′d′，即产生剪切变形。
此楔形体左、右两端面之间的相对扭转角为dφ，矩形abcd的剪应变用γρ表示，则由图8-14中可以看出
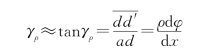
即
式中，
是扭转角φ沿杆长的变化率，即单位长度的扭转角，通常用θ表示，即θ＝
。
于是
对于同一横截面，θ为一常数，可见剪应变γρ与ρ成正比，且沿圆轴的半径按直线规律变化。
2.物理方面
图8-14
将式（8-10）代入上式，得到横截面上与轴线相距为ρ处的剪应力为
式（8-11）表明，在横截面上任一点处的剪应力的大小，与该点到圆心的距离成正比。在圆心处剪应力为零，距圆心越远剪应力越大，距圆心等距离的圆周上各点的剪应力相等，在周边上各点的剪应力最大。剪应力沿直径线的变化规律如图8-15所示。
3.静力学方面
上面已解决了横截面上剪应力的变化规律，但还不能直接按式（8-10）来确定剪应力的大小，这是因为
与扭矩T间的关系尚不清楚。这可从静力学方面来解决。
如图8-16所示，在与圆心相距为ρ的微面积dA上，作用有微剪力τρdA，它对圆心O的微力矩为ρτρdA。在整个横截面上，所有这些微力矩之和应等于该截面的扭矩T，因此
将式（8-11）代入得
积分
即为横截面的极惯性矩，因而式（8-12）可改写为
将式（8-13）代入式（8-11）得
这就是圆轴扭转时横截面上的剪应力计算公式。式中，T为横截面上的扭矩；IP为圆截面对圆心的极惯性矩；ρ为所求应力点至圆心的距离。
由式（8-14）可知，τ与ρ成正比，离圆心越远，τ值越大，圆心处τ＝0。剪应力在横截面上的分布规律如图8-17（a）所示。
实践证明，以上实心圆轴扭转的应力计算公式对空心圆轴也适用，如图8-17（b）所示。只是空心圆轴的极惯性矩IP与实心圆轴的不同。
实心圆轴和空心圆轴的极惯性矩分别为
实心圆轴
空心圆轴
D和d分别为圆形空心截面的外直径和内直径。
图8-15
图8-16
图8-17
【例8-3】 如图8-18所示，受扭圆杆的直径d＝60mm，试求截面1—1上K点的剪应力。
【解】 截面1—1上的扭矩为－2kN·m，K点的剪应力为
计算τ时，扭矩T以绝对值代入。因这里的剪应力正、负无实用意义，一般只计算其绝对值。另外，应注意单位：T的单位为N·m，d和ρ的单位为m，算得的τ为MPa。
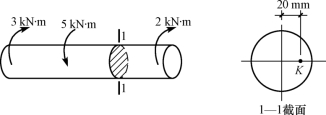
图8-18
有关建筑力学（第3版）的文章
- 详细阅读
-
建筑力学第3版：圆杆扭转变形和刚度条件详细阅读
GIP称为杆件的抗扭刚度，它反映杆件抵抗扭转变形的能力。由得按刚度条件确定d。要使轴同时满足强度和刚度条件，需取轴的直径d＝52mm。......
2023-08-26
-
圆轴扭转：概念解析和应用探讨详细阅读
在日常生活及工程实际中，有很多承受扭转的构件。以扭转变形为主的构件称为轴。在生产实际中圆轴用得较多，本章只研究圆轴的扭转问题。图6-2汽车转向轴图6-3丝锥钻杆图6-4钻探机钻杆汽车方向盘图6-5汽轮机带动发电机转动图6-6电动机带动传动轴转动在两外力偶作用下，轴产生扭转变形，其中杆件任意两截面间相对转动的角度称为扭转角，用φ 表示。......
2023-06-19
-
圆轴扭转强度的条件优化详细阅读
为了保证圆轴在扭转变形中不会因强度不足而发生破坏，应使圆轴横截面上的最大切应力不超过材料的许用切应力，即式称为圆轴扭转的强度条件。案例6-4 如图6-19 所示的阶梯轴，直径分别为d1=40 mm，d2=55 mm，已知C 轮输入转矩MC=1 432.5 N·m，A 轮输出转矩MA=620.8 N·m，轴的转速n=200 r/min，轴材料的许用切应力[τ]=60 MPa，试校核该轴的强度。......
2023-06-19
-
建筑力学（第3版）：矩形截面杆自由扭转详细阅读
在建筑结构中，矩形截面受扭杆一般都处于约束扭转状态。但是，由于约束扭转所引起的正应力可忽略不计，所以可按自由扭转的情况进行计算。这里直接给出矩形截面扭转轴的弹性力学解释的结论：矩形截面扭转轴的横截面上仍然只有剪应力，虽有正应力，但只要h/b的值不太大，正应力的数值很小，可忽略不计。横截面上的最大剪应力发生在长边的中点处。单位长度扭转角全轴的扭转角......
2023-08-26
-
建筑力学（第3版）：轴力图制作详细阅读
当杆件受到多于两个轴向外力的作用时，在杆件的不同横截面上轴力不尽相同。将描述沿杆长各个横截面上轴力变化规律的图形，称为轴力图。画轴力图时，将正的轴力画在轴线上方，负的轴力画在轴线下方。根据上面求出的各段杆轴力的大小及其正负号画出轴力图，如图7-6所示。画轴力图时应注意以下几点：轴力图要与计算简图对齐。标明正负号和数值。在画轴力图时，也可用一条基线表示横截面位置。......
2023-08-26
-
建筑力学（第3版）：轴向拉杆内力-轴力详细阅读
现分析其任一截面m—m上的内力。内力的作用线与杆轴线重合，称为轴向内力，简称轴力，用符号N表示。背离截面的轴力，称为拉力；而指向截面的轴力，称为压力。在求轴力时，通常将轴力假设为拉力方向，这样由平衡条件求出结果的正负号，就可直接代表轴力本身的正负号。根据平衡条件列平衡方程：截面2—2处的杆件轴力N2。......
2023-08-26
-
建筑力学第3版：弯曲剪应力强度计算详细阅读
在梁的强度计算中，必须同时满足正应力和剪应力两个强度条件。在选择梁的截面时，通常是先按正应力强度条件选择截面尺寸，然后再进行剪应力强度校核。对于某些特殊情况，梁的剪应力强度条件也可能起到控制作用。例如，梁的跨度很小，或在支座附近有较大的集中力作用，这时梁可能出现弯矩较小，而剪力却很大的情况，这就必须注意剪应力强度条件是否满足。校核正应力强度及剪应力强度。......
2023-08-26
相关推荐