为解决圆轴扭转的强度问题，在求得横截面上的扭矩之后，还要进一步研究横截面上的应力。在整个横截面上，所有这些微力矩之和应等于该截面的扭矩T，因此将式代入得积分即为横截面的极惯性矩，因而式可改写为将式代入式得这就是圆轴扭转时横截面上的剪应力计算公式。式中，T为横截面上的扭矩；IP为圆截面对圆心的极惯性矩；ρ为所求应力点至圆心的距离。因这里的剪应力正、负无实用意义，一般只计算其绝对值。......
2023-08-26
圆轴扭转内力扭矩-建筑力学（第3版）
【摘要】：在对圆轴进行强度计算之前先要计算出圆轴横截面上的内力——扭矩。根据平衡条件可知，C截面上必存在一个内力偶矩T，与外力偶矩m使左半部保持平衡。此内力偶矩称为扭矩，用T表示。扭矩的单位与力矩相同，常用N·m或kN·m。图8-12与计算轴力的方法类似，用截面法计算扭矩时，通常假定扭矩为正。用截面法分别求出各段上的扭矩。
在对圆轴进行强度计算之前先要计算出圆轴横截面上的内力——扭矩。
1.扭矩计算
设有一圆轴如图8-11（a）所示，在外力偶作用下处于平衡状态，仍用截面法求任意截面C上的内力。
图8-11
将轴在C处截开，取其中一半，如取左半部为研究对象，如图8-11（b）所示。根据平衡条件可知，C截面上必存在一个内力偶矩T，与外力偶矩m使左半部保持平衡。此内力偶矩称为扭矩，用T表示。由∑m＝0得：
求得T＝m。
取右半部为研究对象，也可得相同的结果，如图8-11（c）所示。但扭矩的转向相反，这是因为作用与反作用的关系。扭矩的单位与力矩相同，常用N·m或kN·m。
2.扭矩正负号的规定
为了使由截面的左、右两段轴求得的扭矩具有相同的正负号，对扭矩的正、负做如下规定：采用右手螺旋法则，以右手四指表示扭矩的转向，当拇指的指向与截面外法线方向一致时，扭矩为正号；反之为负号，如图8-12所示。
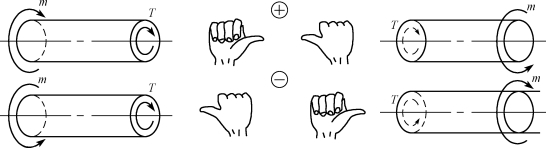
图8-12
与计算轴力的方法类似，用截面法计算扭矩时，通常假定扭矩为正。
3.扭矩图
为了清楚地表示出轴各个截面上扭矩的变化情况，通常将扭矩随截面位置的变化规律绘制成图，称为扭矩图。扭矩图的做法、规则及注意点与轴力图相同。下面以实例说明。
【例8-2】 试作出图8-13（a）所示圆轴的扭矩图。
【解】 （1）用截面法分别求出各段上的扭矩。
假想在截面Ⅰ－Ⅰ处将轴切开，取左段为分离体[图8-13（b）]，根据平衡方程
求得TⅠ＝6kN·m。
假想在截面Ⅱ－Ⅱ处将轴切开，仍取左段为分离体[图8-13（c）]，根据
求得TⅡ＝2kN·m。
假想在截面Ⅲ－Ⅲ处将轴切开，取右段为分离体[图8-13（d）]。根据
求得TⅢ＝3kN·m。
（2）根据求出的各段扭矩值，绘出扭矩图如图8-13（e）所示。
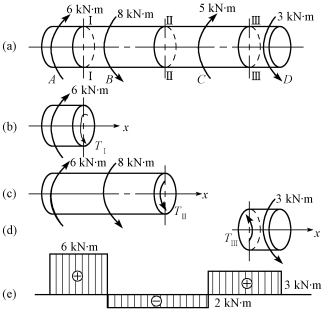
图8-13
有关建筑力学（第3版）的文章
- 详细阅读
-
圆轴扭转横截面内力：探析扭矩现象详细阅读
下面以图6-8所示两端承受外力偶矩M 作用的圆轴为例，说明求任意横截面m-m 上内力的方法。用一假想截面沿m-m 将轴截开，任取一段（如左段），如图6-8所示。由于圆轴是平衡的，因此截取部分也处于平衡状态，根据力偶的性质，横截面m-m 上必有一个内力偶矩与外力偶矩m 平衡，我们把这个内力偶矩称为扭矩，用符号T 表示，单位为N·m 或kN·m。求扭矩时，在截面上均按正向画出扭矩，若所得为负，则说明扭矩转向与假设方向相反。......
2023-06-19
-
建筑力学（第3版）：轴向拉杆内力-轴力详细阅读
现分析其任一截面m—m上的内力。内力的作用线与杆轴线重合，称为轴向内力，简称轴力，用符号N表示。背离截面的轴力，称为拉力；而指向截面的轴力，称为压力。在求轴力时，通常将轴力假设为拉力方向，这样由平衡条件求出结果的正负号，就可直接代表轴力本身的正负号。根据平衡条件列平衡方程：截面2—2处的杆件轴力N2。......
2023-08-26
-
建筑力学第3版：圆杆扭转变形和刚度条件详细阅读
GIP称为杆件的抗扭刚度，它反映杆件抵抗扭转变形的能力。由得按刚度条件确定d。要使轴同时满足强度和刚度条件，需取轴的直径d＝52mm。......
2023-08-26
-
截面法求内力-建筑力学（第3版）详细阅读
图9-4求内力仍采用截面法。力Q和力偶矩M就是梁弯曲时横截面上产生的两种不同形式的内力，力Q称为剪力，力偶矩M称为弯矩。简支梁受载如图9-7所示，试用截面法求截面1—1上的内力。......
2023-08-26
-
圆轴扭转：概念解析和应用探讨详细阅读
在日常生活及工程实际中，有很多承受扭转的构件。以扭转变形为主的构件称为轴。在生产实际中圆轴用得较多，本章只研究圆轴的扭转问题。图6-2汽车转向轴图6-3丝锥钻杆图6-4钻探机钻杆汽车方向盘图6-5汽轮机带动发电机转动图6-6电动机带动传动轴转动在两外力偶作用下，轴产生扭转变形，其中杆件任意两截面间相对转动的角度称为扭转角，用φ 表示。......
2023-06-19
-
圆轴扭转强度的条件优化详细阅读
为了保证圆轴在扭转变形中不会因强度不足而发生破坏，应使圆轴横截面上的最大切应力不超过材料的许用切应力，即式称为圆轴扭转的强度条件。案例6-4 如图6-19 所示的阶梯轴，直径分别为d1=40 mm，d2=55 mm，已知C 轮输入转矩MC=1 432.5 N·m，A 轮输出转矩MA=620.8 N·m，轴的转速n=200 r/min，轴材料的许用切应力[τ]=60 MPa，试校核该轴的强度。......
2023-06-19
-
建筑力学（第3版）：矩形截面杆自由扭转详细阅读
在建筑结构中，矩形截面受扭杆一般都处于约束扭转状态。但是，由于约束扭转所引起的正应力可忽略不计，所以可按自由扭转的情况进行计算。这里直接给出矩形截面扭转轴的弹性力学解释的结论：矩形截面扭转轴的横截面上仍然只有剪应力，虽有正应力，但只要h/b的值不太大，正应力的数值很小，可忽略不计。横截面上的最大剪应力发生在长边的中点处。单位长度扭转角全轴的扭转角......
2023-08-26
相关推荐