首页理论教育建筑力学第3版：相对变形、泊松比的测定方法

建筑力学第3版：相对变形、泊松比的测定方法

2023-08-26 理论教育版权反馈

【摘要】：绝对变形的大小只反映杆的总变形量，而无法说明杆的变形程度。因此，为了度量杆的变形程度，还需计算单位长度内的变形量。对于轴力为常量的等截面直杆，其变形处处相等。试验表明，当拉（压）杆内应力不超过某一限度时，横向线应变ε′与纵向线应变ε之比的绝对值为一常数，即μ称为横向变形因数或泊松比，是无因次的量，其数值随材料而异，也是通过试验测定的。

绝对变形的大小只反映杆的总变形量，而无法说明杆的变形程度。因此，为了度量杆的变形程度，还需计算单位长度内的变形量。对于轴力为常量的等截面直杆，其变形处处相等。可将Δl除以l，Δd除以d表示单位长度的变形量，即

pagenumber_ebook=99,pagenumber_book=87

ε称为纵向线应变，ε′称为横向线应变。应变是单位长度的变形，是无因次的量。由于Δl与Δd具有相反符号，因此ε与ε′也具有相反的符号。将式（7-16）代入式（7-18），得胡克定律的另一表达形式为

显然，式（7-20）中的纵向线应变ε和横截面上正应力的正负号也是相对应的。式（7-20）是经过改写后的胡克定律，它不仅适用于拉（压）杆，而且还可以更普遍地用于所有的单轴应力状态，故通常又称为单轴应力状态下的胡克定律。

试验表明，当拉（压）杆内应力不超过某一限度时，横向线应变ε′与纵向线应变ε之比的绝对值为一常数，即

μ称为横向变形因数或泊松比，是无因次的量，其数值随材料而异，也是通过试验测定的。弹性模量E和泊松比μ都是材料的弹性常数。几种常用材料的E和μ值可参阅表7-1。

表7-1　常用材料的E和μ的数值

pagenumber_ebook=99,pagenumber_book=87

必须指出，当沿杆长度为非均匀变形时，式（7-18）并不反映沿长度各点处的纵向线应变。对于各处变形不均匀的情形（图7-12），则必须考核杆件上沿轴向的微段dx的变形，并以dx的相对变形来度量杆件局部的变形程度。这时有

pagenumber_ebook=99,pagenumber_book=87

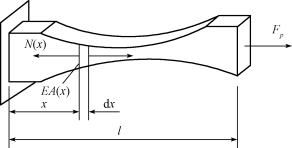
pagenumber_ebook=100,pagenumber_book=88

图7-12

可见，无论变形均匀还是不均匀，正应力与正应变之间的关系都是相同的。

【例7-4】　已知阶梯形直杆受力如图7-13（a）所示，材料的弹性模量E＝200GPa，杆各段的横截面面积分别为AAB＝ABC＝1500mm2，ACD＝1000mm2。要求：

（1）作轴力图；

（2）计算杆的总伸长量。

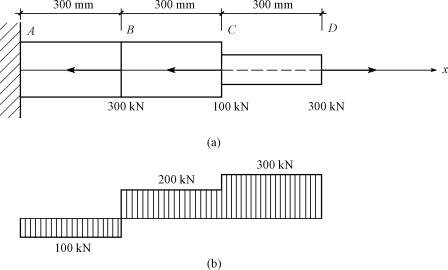
pagenumber_ebook=100,pagenumber_book=88

图7-13

【解】　（1）画轴力图。因为在A、B、C、D处都有集中力作用，所以AB、BC和CD三段杆的轴力各不相同。应用截面法得

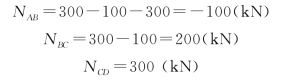
pagenumber_ebook=100,pagenumber_book=88

轴力图如图7-13（b）所示。

（2）求杆的总伸长量。因为杆各段轴力不等，且横截面面积也不完全相同，因而必须分段计算各段的变形，然后求和。各段杆的轴向变形分别为

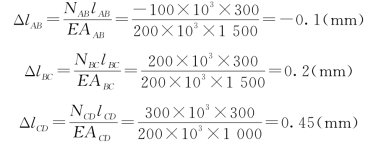
pagenumber_ebook=100,pagenumber_book=88

杆的总伸长量为

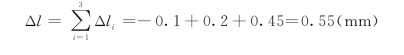
pagenumber_ebook=101,pagenumber_book=89