由式（7-6）、式（7-7）可知，轴向拉压杆在斜截面上有正应力和剪应力，它们的大小随截面的方位α角的变化而变化。当α＝0°时，正应力达到最大值：由此可见，拉压杆的最大正应力发生在横截面上。当α＝90°时，σα＝τα＝0，这表明在平行于杆轴线的纵向截面上无任何应力。......
2023-08-26
轴向拉（压）杆横截面上的应力|建筑力学（第3版）
【摘要】：由此可得，横截面上各点处的正应力σ大小相等[图7-7]。若杆的轴力为N，横截面面积为A，则正应力为应力的单位为帕斯卡（简称帕），1帕＝1牛顿/平方米，或表示为1Pa＝1N/m2。由于前面已规定了轴力的正负号，由式（7-1）可知，正应力也随轴力N而有正负之分，即拉应力为正，压应力为负。直杆的横截面面积A＝10cm2，试计算各段横截面上的正应力。图7-8用截面法求出各段轴力：由式（7-1）计算各段的正应力值为
图7-7（a）所示的等直杆，在杆件的外表面画上一系列与轴线平行的纵向线和与轴线垂直的横向线。施加轴向拉力P后，杆发生变形，所有的纵向线均产生同样的伸长，所有的横向线均仍保持为直线，且仍与轴线正交[图7-7（b）]。
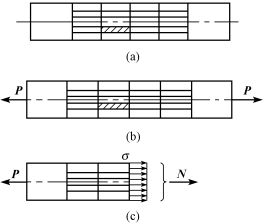
图7-7
根据上述试验现象，对杆件的内部变形可做出如下假设：
（1）平面假设。若将各条横线看作一个横截面，则杆件横截面在变形以后仍为平面且与杆轴线垂直，任意两个横截面只是做相对平移。
（2）若将各纵向线看作杆件由许多纤维组成，根据平面假设，任意两横截面之间的所有纤维的伸长都相同，即杆件横截面上各点处的变形都相同，因此推断它们受的力也相等。
由此可得，横截面上各点处的正应力σ大小相等[图7-7（c）]。若杆的轴力为N，横截面面积为A，则正应力为
应力的单位为帕斯卡（简称帕），1帕＝1牛顿/平方米，或表示为1Pa＝1N/m2。由于此单位较小，常用兆帕（MPa）或吉帕（GPa）表示（1MPa＝106Pa，1GPa＝109Pa）。
当杆件受轴向压缩时，式（7-1）同样适用。由于前面已规定了轴力的正负号，由式（7-1）可知，正应力也随轴力N而有正负之分，即拉应力为正，压应力为负。
【例7-3】 一直杆的受力情况如图7-8所示。直杆的横截面面积A＝10cm2，试计算各段横截面上的正应力。
图7-8
【解】 （1）用截面法求出各段轴力：
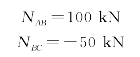
（2）由式（7-1）计算各段的正应力值为
有关建筑力学（第3版）的文章
- 详细阅读
-
轴向拉压对横截面应力的影响详细阅读
要解决轴向拉压杆的强度问题，不但要知道杆件的内力，还必须知道内力在截面上的分布规律。下面用这种方法推导轴向拉压杆的应力计算公式。由于拉压杆的轴力是垂直于横截面的，故与它相应的分布内力也必然垂直于横截面，由此可知，轴向拉杆横截面上只有正应力，而没有剪应力。由此可得出结论：轴向拉伸时，杆件横截面上各点处只产生正应力，且大小相等[图5-9]，即式中 N——杆件横截面上的轴力；A——杆件的横截面面积。......
2023-06-16
-
建筑力学第3版-临界应力总图-压杆计算公式详细阅读
如果将压杆的临界应力根据其柔度不同而分别计算的情况用一个简图来表示，该图形就称为压杆的临界应力总图。图11-9与图11-10即某塑性材料的临界应力总图。由临界应力总图可以看出，Q235钢应在λ＝0～123时用抛物线形经验公式计算临界应力，在λ＞123时用欧拉公式计算临界应力。......
2023-08-26
-
《建筑力学第3版》-细长压杆临界力计算详细阅读
以上讨论的是两端铰支的细长压杆的临界力计算。对于其他支承形式的压杆，也可用同样方法导出其临界力的计算公式。因此，可将两端铰支约束压杆的挠曲线形状取为基本情况，而将其他杆端约束条件下压杆的挠曲线形状与之进行对比，从而得到相应杆端约束条件下压杆临界力的计算公式。表11-1各种支承约束条件下等截面压杆临界力的欧拉公式以上讨论的都是理想的支承情况。现分别计算两种截面杆的临界力。......
2023-08-26
-
轴向拉压对杆的变形：胡克定律简析详细阅读
反之，在轴向压力作用下，将引起轴向的缩短和横向的增大。因此，必须研究杆件的变形。与上述两种绝对变形相对应的纵向线应变为横向线应变线应变表示的是杆件的相对变形。即式（4-5）称为虎克定律。常数E 称为材料的弹性模量，其值随材料而异，可由试验测定。试求整个杆的变形量。......
2023-06-19
-
轴向拉（压）杆的强度条件和计算方法优化详细阅读
由式（5-1）可知，拉（压）杆的工作应力，为了保证构件能安全正常地工作，则杆内最大的工作应力不得超过材料的许用应力。即式（5-8）称为拉（压）杆的强度条件。在轴向拉（压）杆中，产生最大正应力的截面称为危险截面。应用强度条件式（5-8）可以解决轴向拉（压）杆强度计算的三类问题。如，表示杆件的强度是满足要求的，否则不满足强度条件。......
2023-06-16
-
压杆稳定条件的应用与建筑力学（第3版）相关详细阅读
即已知压杆的几何尺寸、所用材料及支承条件，按稳定条件计算其能够承受的许用荷载值F。在稳定条件式中，已知φ后才能标出A值，但在杆件尺寸未确定之前，无法确定λ值，因而也就无法确定φ值，故可采用试算的方法。然后，根据截面尺寸及杆长计算出柔度λ，由λ查出φ，再以算得的面积A和查得的φ值验算其是否满足稳定条件。......
2023-08-26
-
压杆柔度与临界应力的欧拉公式计算方法详细阅读
于是临界应力可写为令则上式为计算压杆临界应力的欧拉公式，式中λ称为压杆的柔度。从式（9-3）还可以看出，压杆的柔度值越大，则其临界应力越小，压杆就越容易失稳。因此，欧拉公式的适用范围应当是压杆的临界应力σcr不超过材料的比例极限σP，即有若设λP为压杆的临界应力达到材料的比例极限σP时的柔度值，则故欧拉公式的适用范围为上式表明，当压杆的柔度不小于λP时，才可以应用欧拉公式计算临界力或临界应力。......
2023-06-16
相关推荐