首页理论教育建筑力学：重心坐标公式及计算方法

建筑力学：重心坐标公式及计算方法

2025-09-30 理论教育版权反馈

【摘要】：为确定物体重心的位置，将物体看作由微体积ΔV1，ΔV2，ΔV3，…所以，均质物体的重心就是其几何中心，称为形心。对于均质物体，形心坐标公式（6-4）也可写成积分形式为：式中dV——均质物体微小部分的体积；x、y、z——物体微小部分的空间坐标；V——均质物体的总体积。

为确定物体重心的位置，将物体看作由微体积ΔV1，ΔV2，ΔV3，…，ΔVn组成，物体的总体积为

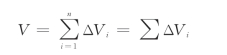
pagenumber_ebook=81,pagenumber_book=69

设每一微体积单位体积的重力为γi，则ΔV1的重力为γ1ΔV1，ΔV2的重力为γ2ΔV2，…，ΔVn的重力为γnΔVn。取直角坐标系如图6-1所示。其中，y轴铅垂向上，ΔV1的作用点位置为C1，ΔV2的作用点位置为C2，…，ΔVn的作用点位置为Cn。各微体积的重力作用线均平行于y轴，视为分力。则物体所受的重力的合力为

根据合力矩定理，可以求得合力作用点（即重心）的位置，即对x轴取矩：

pagenumber_ebook=82,pagenumber_book=70

由此可得

pagenumber_ebook=82,pagenumber_book=70

同理，对z轴取矩，可得

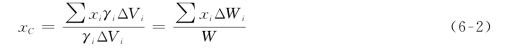
pagenumber_ebook=82,pagenumber_book=70

当物体视为刚体时，无论物体在空间中处于何种位置，也无论物体如何放置，其重心在物体内的位置都是固定的。因而，若将图6-1中的空间坐标系绕z轴旋转90°（图6-2）时，可得重心在y轴方向的位置。

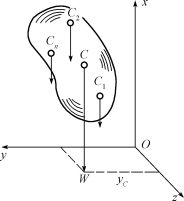
pagenumber_ebook=82,pagenumber_book=70

pagenumber_ebook=82,pagenumber_book=70

图6-1

pagenumber_ebook=82,pagenumber_book=70

图6-2

对于均质物体，微体积单位体积的重力相等，即γ＝γ1＝γ2＝γ3＝…＝γn，由式（6-1）～式（6-3）可得均质物体的重心坐标公式为

pagenumber_ebook=82,pagenumber_book=70 (https://www.chuimin.cn)

由式（6-4）可以算出，均质物体的重心与重力无关。所以，均质物体的重心就是其几何中心，称为形心。对于均质物体，其重心和形心重合在一点上。

如果将物体分割的份数无数多，且每份的体积无限小，在极限情况下，则式（6-1）～式（6-3）可写成积分形式。

pagenumber_ebook=82,pagenumber_book=70

式中　dW——物体微小部分的重量（或所受的重力）；

　　　x、y、z——物体微小部分的空间坐标；

　　　W——物体的总重力。

对于均质物体，形心坐标公式（6-4）也可写成积分形式为：

pagenumber_ebook=83,pagenumber_book=71

式中　dV——均质物体微小部分的体积；

　　　x、y、z——物体微小部分的空间坐标；

　　　V——均质物体的总体积。

对于均质、等厚的薄平板，计算形心坐标时，可将坐标面xOy建立在与板平行的板的中间平面上（图6-3），用δ表示其厚度，ΔAi表示微面积，则由式（6-4）得形心坐标计算公式如下：

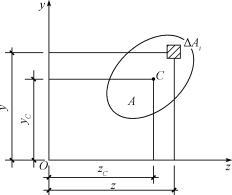
pagenumber_ebook=83,pagenumber_book=71

图6-3

pagenumber_ebook=83,pagenumber_book=71

同理，当微面积ΔAi→0时，则可用积分形式表示如下：

pagenumber_ebook=83,pagenumber_book=71