几何法求解平面汇交力系的合力具有直观、明了、简捷的优点，但其精确度较差，在力学计算时多用解析法。物体在平面汇交力系作用下处于平衡的充分必要条件是：合力R的大小等于零。即要使式（2-8）成立，则：式（2-9）表明平面汇交力系平衡的解析条件是：力系中各分力在任意两个坐标轴上投影的代数和分别等于零。式（2-9）称为平面汇交力系的平衡方程。代入相应数据解得负号表示受力图中的方向与实际相反，在斜杆中实为压力。......
2023-08-26
建筑力学第三版：空间汇交力系平衡
【摘要】：空间汇交力系合成为一个合力，若物体在空间汇交力系作用下而处于平衡状态，其合力必须为零。因此，空间汇交力系平衡的充分必要条件是：空间汇交力系的合力为零，即要使上式成立，必须同时满足因此，空间汇交力系平衡的充分必要条件是：力系中所有各力在三个坐标轴中每一轴上的投影的代数和为零。式（5-8）称为空间汇交力系的平衡方程，有三个独立的方程，可解三个未知量。根据空间汇交力系平衡方程解得
空间汇交力系合成为一个合力，若物体在空间汇交力系作用下而处于平衡状态，其合力必须为零。因此，空间汇交力系平衡的充分必要条件是：空间汇交力系的合力为零，即
要使上式成立，必须同时满足
因此，空间汇交力系平衡的充分必要条件是：力系中所有各力在三个坐标轴中每一轴上的投影的代数和为零。式（5-8）称为空间汇交力系的平衡方程，有三个独立的方程，可解三个未知量。
【例5-3】 杆AB、AC和AD在A点由球铰连在一起，B、C、D点在半径为3m的圆周上，A点承受5kN的力，方向与y轴平行，如图5-10所示，各杆自重不计，求各杆所受的力。
【解】 考虑A点，作用有力的大小为5kN，FAC、FAB、FAD汇交于A点，构成空间汇交力系。计算各力在坐标轴的投影，设∠ACO＝α。
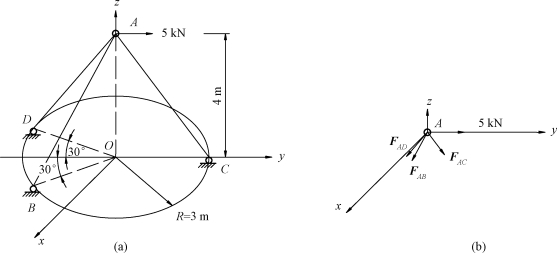
图5-10
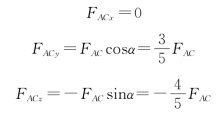
杆AB、AD的投影采用二次投影法计算
根据空间汇交力系平衡方程
解得
【例5-4】 匀质板重G＝2kN，重心在O点，由三根绳子吊起，如图5-11（a）所示，试计算绳子的拉力。
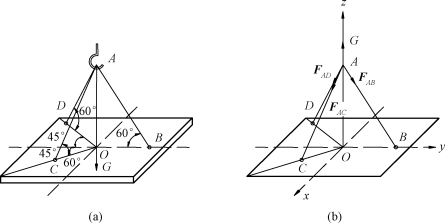
图5-11
【解】 板重力G，三根绳子的拉力FAB、FAC、FAD是汇交于A点的空间汇交力系，建立图5-11（b）所示的坐标系，计算各力在坐标轴的投影。
根据空间汇交力系平衡方程
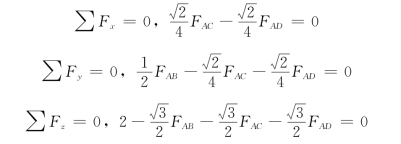
解得
有关建筑力学（第3版）的文章
- 详细阅读
- 详细阅读
- 详细阅读
-
建筑力学：平面平行力系平衡方程详细阅读
如前所述，力系中各力的作用线在同一平面内且相互平行，这样的力系称为平面平行力系。平面汇交力系、平面力偶系、平面平行力系都是平面任意力系的特殊情况。下面导出平面平行力系的平衡方程。于是，平面平行力系只有两个独立的平衡方程，即图4-8平面平行力系的平衡方程，也可以写成二力矩式的形式，即式中，A、B两点的连线不与力线平行。利用平面平行力系的平衡方程，可求解两个未知量。......
2023-08-26
-
建筑力学第3版：平面汇交力合成几何法详细阅读
在第一章中，已对几何法进行了介绍，知道了两个汇交于一点的力F1和F2如何应用力的平行四边形法则和三角形法则求它们的合力R。设作用于物体上A点的力F1、F2、F3、F4组成平面汇交力系，现求其合力，如图2-2所示。这种由各分力和合力构成的多边形abcde称为力多边形。这种求合力矢的几何作图法被称为力多边形法。拉力F1、F2、F3的作用力汇交于O点，构成平面汇交力系。......
2023-08-26
-
建筑力学第三版：材料的拉伸力学性能详细阅读
当应力不超过比例极限σp时，σ和ε成正比，直线Oa的斜率即材料的弹性模量E。在此阶段材料失去了抵抗变形的能力，产生显著的塑性变形。经过屈服阶段后，材料又恢复了抵抗变形的能力，此时，增加荷载才会继续变形，这个阶段称为强化阶段。......
2023-08-26
-
解析法：另一种常用的求解平面汇交力系合成的方详细阅读
求解平面汇交力系合成的另一种常用方法是解析法。图2-3力的分解图2-4各力在坐标轴上的投影解：根据式（2-3）、式（2-4），列表计算如下：2.合力投影定理为了用解析法求平面汇交力系的合力，必须先讨论合力及其分力在同一坐标轴上投影的关系。图2-8例2-2图解析法。......
2023-06-16
-
建筑力学第五节：物体系统的平衡详细阅读
图4-13求解物体系统的平衡问题具有重要的实际意义。当物体系统处于平衡状态时，该体系中的每一个物体也必定处于平衡状态。对由n个物体组成的物体系统，则共有3n个独立的平衡方程。假如物体系统中有受平面汇交力系或平面平行力系作用的物体，独立的平衡方程数目相应减少。按照上述方法求解物体系统的平衡问题，在理论上并不困难。求解物体系统的平衡问题，关键在于恰当地选取研究对象，正确地选取投影轴和矩心，列出适当的平衡方程。......
2023-08-26
相关推荐