首页理论教育建筑力学（第3版）：力平移定理简化方法及结果

建筑力学（第3版）：力平移定理简化方法及结果

2025-09-30 理论教育版权反馈

【摘要】：根据力的平移定理，将各力平移到O点，其结果得到一个作用于O点的平面汇交力系，，…附加的平面力偶系可以合成一合力偶，其力偶矩MO称为原力系向O点简化的主矩。这个力作用在简化中心，它的矢量称为原力系的主矢，并等于原力系中各力的矢量和；这个力偶的力偶矩称为原力系对简化中心的主矩，并等于原力系中各力对简化中心之矩的代数和。

设刚体上作用有平面一般力系F1，F2，…，Fn，各力的作用点分别为A1，A2，…，An，如图4-3所示。在力系的作用面内任选一点O，称为简化中心。根据力的平移定理，将各力平移到O点，其结果得到一个作用于O点的平面汇交力系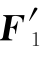 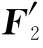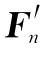pagenumber_ebook=57,pagenumber_book=45 ，，…，和一个附加的平面力偶系，其力偶矩分别为m1，m2，…，mn。

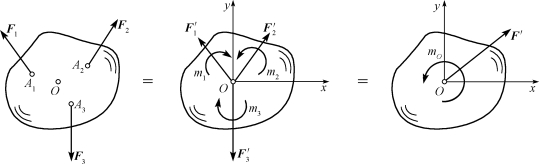
pagenumber_ebook=57,pagenumber_book=45

图4-3

其中平面汇交力系中各力的大小和方向分别与原力系中对应的各力相同，即

各附加的力偶矩分别等于原力系中各力对简化中心O点之矩，即

由平面汇交力系合成的理论可知，可合成为一个作用于O点的力，这个力的矢量F′称为原力系的主矢。则有：

在计算主矢F′时，引进参考直角坐标系xOy，根据合力投影定理，可得：

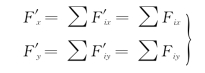pagenumber_ebook=57,pagenumber_book=45 (https://www.chuimin.cn)

主矢的大小：

主矢与x轴所夹的锐角：

pagenumber_ebook=58,pagenumber_book=46

指向由F′x、F′y的正负号判断。

附加的平面力偶系可以合成一合力偶，其力偶矩MO称为原力系向O点简化的主矩。显然

所以，对平面任意力系向任一点简化的结果可以总结如下：平面一般力系向作用面内任一点简化的结果，是一个力和一个力偶。这个力作用在简化中心，它的矢量称为原力系的主矢，并等于原力系中各力的矢量和；这个力偶的力偶矩称为原力系对简化中心的主矩，并等于原力系中各力对简化中心之矩的代数和。

应当注意的是，作用于简化中心的力F′一般并不是原力系的合力，力偶矩为MO的力偶也不是原力系的合力偶，只有F′与MO两者相结合才与原力系等效。

由于主矢等于原力系中各力的矢量和，因此主矢F的大小和方向与简化中心的位置无关。而主矩等于原力系中各力对简化中心之矩的代数和，取不同的点作为简化中心，各力的力臂都要发生变化，则各力对简化中心的力矩也会改变。因此，主矩一般随着简化中心的位置改变而改变（即主矩与简化中心有关）。