力对点的矩是很早以前人们在使用杠杆、滑车、绞盘等机械搬运或提升重物时所形成的一个概念。若改变力的作用方向，则扳手的转动方向就会发生改变，因此，用F与d的乘积再冠以适当的正负号来表示力F使物体绕O点转动的效应，并称为力F对O点的矩，简称力矩，以符号MO表示，即O点称为转动中心，简称矩心。式中的正负号表示力矩的转向。分别计算图3-3所示的F1、F2对O点的力矩。......
2023-06-16
力对点的矩及其作用-建筑力学第3版
【摘要】：力对点的矩是一个代数量，其绝对值等于力的大小与力臂之积，其正负可作如下规定：力使物体绕矩心逆时针转动时取正号；反之取负号。力F对O点的矩，以符号mO表示，即O点称为转动中心，简称矩心。试求两个力对A点的力矩。图3-3二力对A点的力矩分别为计算结果表明，力F2使物体绕A点转动的效果大于力F1所产生的转动效果，板将绕A点顺时针方向转动。
力对点的矩是很早以前人们在使用杠杆、滑轮、绞盘等机械搬运或提升重物时所形成的一个概念。现以扳手拧螺母为例来加以说明。如图3-1所示，在扳手的A点施加力F，将使扳手和螺母一起绕螺栓中心O转动，也就是说，力有使物体（扳手）产生转动的效应。实践经验表明，扳手的转动效果不仅与力F的大小有关，而且还与O点到力作用线的垂直距离d有关。当d值保持不变时，力F越大，转动越快。当力F不变时，d值越大，转动也越快。若改变力的作用方向，则扳手的转动方向就会发生改变，因此，用F与d的乘积和合适的正负号来表示力F使物体绕O点转动的效应。
图3-1
一般情况下，物体受力F作用（图3-2），力F使物体绕平面上任意点的转动效果，可用力F对O点的力矩来度量。所以，可将力对点的矩定义为：力对点的矩是力使物体绕点转动效果的度量。力对点的矩是一个代数量，其绝对值等于力的大小与力臂之积，其正负可作如下规定：力使物体绕矩心逆时针转动时取正号；反之取负号。
力F对O点的矩，以符号mO（F）表示，即
O点称为转动中心，简称矩心。矩心O到力作用线的垂直距离d称为力臂。
由图3-2可以看出，力对点的矩还可用以矩心为顶点，以力矢量为底边所构成的三角形的面积的两倍来表示。即
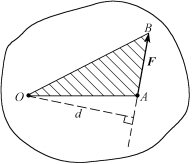
图3-2
在平面力系中，力矩或为正值，或为负值，因此，力矩可视为代数量。
显然，力矩在下列两种情况下等于零：一是力等于零；二是力臂等于零，就是力的作用线通过矩心。力矩的单位是牛顿·米（N·m）或千牛顿·米（kN·m）。
【例3-1】 矩形板的边长a＝0.3m，b＝0.2m，放置在水平面上。给定力F1＝40N，F2＝50N，二力与长边的夹角α＝30°，如图3-3所示。试求两个力对A点的力矩。如果A点是一转轴，试判断在此二力的作用下矩形板绕A点转动的方向。
图3-3
【解】 二力对A点的力矩分别为
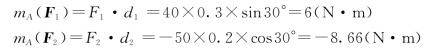
计算结果表明，力F2使物体绕A点转动的效果大于力F1所产生的转动效果，板将绕A点顺时针方向转动。
【例3-2】 分别计算图3-4所示的F1、F2对O点的力矩。
【解】 由式（3-1），有：
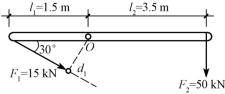
图3-4
有关建筑力学（第3版）的文章
- 详细阅读
-
建筑力学（第3版）：力对轴的矩合力矩定理详细阅读
乘积Fxy·d是力Fxy对O点的力矩值。力对某轴之矩，等于力在与该轴垂直平面上的分力对该轴与垂直平面交点之矩。图5-4当力与某轴平行或相交时，力对该轴之矩为零。图5-5因为力F与z轴相交，它对z轴之矩为零，即将力F分解为xy平面上的分力Fxy和z轴方向的分力Fz，由于分力Fxy与x、y轴都相交，它对x、y轴之矩均为零。根据合力矩定理，有......
2023-08-26
-
《建筑力学第3版》-细长压杆临界力计算详细阅读
以上讨论的是两端铰支的细长压杆的临界力计算。对于其他支承形式的压杆，也可用同样方法导出其临界力的计算公式。因此，可将两端铰支约束压杆的挠曲线形状取为基本情况，而将其他杆端约束条件下压杆的挠曲线形状与之进行对比，从而得到相应杆端约束条件下压杆临界力的计算公式。表11-1各种支承约束条件下等截面压杆临界力的欧拉公式以上讨论的都是理想的支承情况。现分别计算两种截面杆的临界力。......
2023-08-26
-
建筑力学（第3版）：轴向拉杆内力-轴力详细阅读
现分析其任一截面m—m上的内力。内力的作用线与杆轴线重合，称为轴向内力，简称轴力，用符号N表示。背离截面的轴力，称为拉力；而指向截面的轴力，称为压力。在求轴力时，通常将轴力假设为拉力方向，这样由平衡条件求出结果的正负号，就可直接代表轴力本身的正负号。根据平衡条件列平衡方程：截面2—2处的杆件轴力N2。......
2023-08-26
-
建筑力学第3版：平面汇交力合成几何法详细阅读
在第一章中，已对几何法进行了介绍，知道了两个汇交于一点的力F1和F2如何应用力的平行四边形法则和三角形法则求它们的合力R。设作用于物体上A点的力F1、F2、F3、F4组成平面汇交力系，现求其合力，如图2-2所示。这种由各分力和合力构成的多边形abcde称为力多边形。这种求合力矢的几何作图法被称为力多边形法。拉力F1、F2、F3的作用力汇交于O点，构成平面汇交力系。......
2023-08-26
-
建筑力学研究任务和内容，建筑力学第3版详细阅读
建筑力学的任务是研究结构的几何组成规律，以及在荷载作用下结构和构件的强度、刚度和稳定性问题。具体来说，建筑力学将讨论下列几个方面的内容：力系的简化和力系平衡问题。......
2023-08-26
-
建筑力学（第3版）：力平移定理简化方法及结果详细阅读
根据力的平移定理，将各力平移到O点，其结果得到一个作用于O点的平面汇交力系，，…附加的平面力偶系可以合成一合力偶，其力偶矩MO称为原力系向O点简化的主矩。这个力作用在简化中心，它的矢量称为原力系的主矢，并等于原力系中各力的矢量和；这个力偶的力偶矩称为原力系对简化中心的主矩，并等于原力系中各力对简化中心之矩的代数和。......
2023-08-26
-
力法基本原理-建筑力学（第3版）详细阅读
力法是计算超静定结构最基本的方法，下面先用一个例子说明力法的基本原理。这个静定梁称为原超静定梁的基本结构。若用Δ1q和Δ11分别表示荷载q和多余未知力X1单独作用下基本结构在X1作用处沿X1方向产生的位移，则由叠加原理根据位移条件可得下列方程：若X1＝1，在X1方向产生的位移为δ11，则有Δ11＝δ11X1，于是式可以写成这就是求解多余未知力的补充方程，称为力法方程。......
2023-08-26
相关推荐