计算力在空间直角坐标轴上的投影包括直接投影法和二次投影法两种方法。力的投影指向与坐标轴的正向一致时投影为正；反之为负。若已知力在三个坐标轴上的投影Fx、Fy、Fz，则力的大小和方向余弦为在一个正立方体上作用有三个力F1、F2和F3，如图5-8所示，已知F1＝3kN，F2＝2kN，F3＝1kN，计算这三个力在坐标轴x、y、z上的投影。......
2023-08-26
直角坐标轴上的投影|建筑力学（第3版）
【摘要】：从力F的两端点A和B分别向x轴作垂线，得垂足a和b，并在x轴上得线段ab，线段ab的长度称为力F在x轴上的投影的大小，用Fx表示。力在平面直角坐标轴上的投影计算，在力学计算中应用非常普遍，必须熟练掌握。
设力F作用在物体上某点A处，如图2-5所示。通过力F所在平面内的任意点O作平面直角坐标系xOy。从力F的两端点A和B分别向x轴作垂线，得垂足a和b，并在x轴上得线段ab，线段ab的长度称为力F在x轴上的投影的大小，用Fx表示。同样的方法也可以确定力F在y轴上的投影的大小为线段a′b′的长度，用Fy表示。投影为代数量，并规定：当力的始端投影到终端的投影方向与投影轴的正向一致时，力的投影取正值；反之，当力的始端投影到终端的投影方向与投影轴的正向相反时，力的投影取负值。
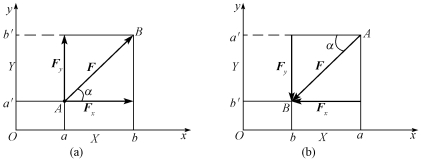
图2-5
从图2-5中的几何关系得出投影的计算公式为
式中，α为力F与x轴所夹的锐角，Fx和Fy的正负号可按上述规定确定。
由式（2-4）可知，当力与坐标轴垂直时，力在该轴上的投影为零；当力与坐标轴平行时，力在该轴上投影的绝对值与该力的大小相等。
如果已知力F的大小及方向，就可以用式（2-4）方便地计算出投影Fx和Fy；反之，如果已知力F在x轴和y轴上的投影Fx和Fy，则由图2-5中的几何关系，可用式（2-5）确定力F的大小和方向，即
式中，α为力F与x轴所夹的锐角，力F的具体方向可由Fx、Fy的正负号确定。
应当注意的是，力的投影和分力是两个不同的概念。力的投影是标量，它只有大小和正负；而力的分力是矢量，有大小和方向。
力在平面直角坐标轴上的投影计算，在力学计算中应用非常普遍，必须熟练掌握。
【例2-2】 已知力F1＝100N，F2＝50N，F3＝80N，F4＝60N，各力的方向如图2-6所示，试计算各力在x轴和y轴上的投影。
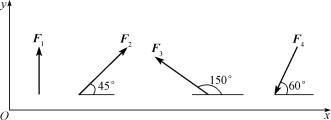
图2-6
【解】 各力在x轴和y轴上的投影分别为
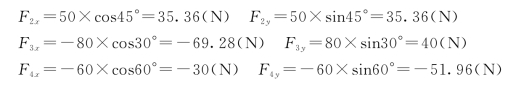
有关建筑力学（第3版）的文章
- 详细阅读
-
直角投影及应用详细阅读
但当角的两边同时为某投影面平行线时，它在该面上的投影等于原角。根据直角投影的特性，可以解决投影图中有关垂直的问题，以及点到直线的距离等问题。图3-30直角的投影性质例3-10过点A作直线与CD垂直相交。根据直角投影特性可知，与正平线垂直的直线，其正面投影必与正平线的正面投影垂直。由于AB是一般位置直线，不能直接利用直角投影特性，但可用换面法先将AB变为投影面平行线。......
2023-06-28
-
建筑力学研究任务和内容，建筑力学第3版详细阅读
建筑力学的任务是研究结构的几何组成规律，以及在荷载作用下结构和构件的强度、刚度和稳定性问题。具体来说，建筑力学将讨论下列几个方面的内容：力系的简化和力系平衡问题。......
2023-08-26
-
建筑力学（第3版）-结构的计算简图详细阅读
在选取其计算简图时，可根据实际构造和约束情况进行。在计算简图中，通常可将结点分为铰结点和刚结点两种。事实上，结构在荷载作用下，杆件之间所产生的转动也相当小，所以，该结点应视为铰结点。因而，刚结点对杆端有阻止相对转动的约束力存在，既除产生杆端轴力和剪力外，还引起杆端弯矩。计算时这种结点应视为刚结点，其计算简图如图1-23所示。......
2023-08-26
- 详细阅读
-
建筑力学（第3版）：轴力图制作详细阅读
当杆件受到多于两个轴向外力的作用时，在杆件的不同横截面上轴力不尽相同。将描述沿杆长各个横截面上轴力变化规律的图形，称为轴力图。画轴力图时，将正的轴力画在轴线上方，负的轴力画在轴线下方。根据上面求出的各段杆轴力的大小及其正负号画出轴力图，如图7-6所示。画轴力图时应注意以下几点：轴力图要与计算简图对齐。标明正负号和数值。在画轴力图时，也可用一条基线表示横截面位置。......
2023-08-26
-
材料压缩时的力学性能在建筑力学中（第3版）详细阅读
一般塑性材料都存在上述情况，但有些塑性材料压缩与拉伸时的屈服点的应力不同，如铬钢、硅合金钢。（二）铸铁的压缩试验图7-22所示为铸铁压缩时的应力-应变曲线。木材是各向异性材料，其力学性能具有方向性，顺纹方向的强度要比横纹方向高得多，而且其抗拉强度高于抗压强度。......
2023-08-26
- 详细阅读
相关推荐