求解平面汇交力系合成的另一种常用方法是解析法。图2-3力的分解图2-4各力在坐标轴上的投影解：根据式（2-3）、式（2-4），列表计算如下：2.合力投影定理为了用解析法求平面汇交力系的合力，必须先讨论合力及其分力在同一坐标轴上投影的关系。图2-8例2-2图解析法。......
2025-09-29
建筑力学第3版：平面汇交力合成几何法
【摘要】：在第一章中，已对几何法进行了介绍，知道了两个汇交于一点的力F1和F2如何应用力的平行四边形法则和三角形法则求它们的合力R。设作用于物体上A点的力F1、F2、F3、F4组成平面汇交力系，现求其合力，如图2-2所示。这种由各分力和合力构成的多边形abcde称为力多边形。这种求合力矢的几何作图法被称为力多边形法。拉力F1、F2、F3的作用力汇交于O点，构成平面汇交力系。
在第一章中，已对几何法进行了介绍，知道了两个汇交于一点的力F1和F2如何应用力的平行四边形法则和三角形法则求它们的合力R。当要求用几何法求更多汇交于一点的力的合力时，也可以此为基础进行求解，下面举例进行说明。
设作用于物体上A点的力F1、F2、F3、F4组成平面汇交力系，现求其合力，如图2-2（a）所示。应用力的三角形法则，首先将F1、F2合成得R1，然后将R1与F3合成得R2，最后将R2与F4合成得R，力R就是原汇交力系F1、F2、F3、F4的合力，图2-2（b）所示即是此汇交力系合成的几何示意图，矢量关系的数学表达式为
实际作图时，可以不必画出图中虚线所示的中间合力R1和R2，只要按照一定的比例尺将表达各力矢量的有向线段首尾相接，就会形成一个不封闭的多边形，如图2-2（c）所示。然后再画一条从起点指向终点的矢量R，即原汇交力系的合力，如图2-2（d）所示。这种由各分力和合力构成的多边形abcde称为力多边形。按照与各分力同样的比例，封闭边的长度表示合力的大小，合力的方向与封闭边的方向一致，指向则由力多边形的起点至终点，合力的作用线通过汇交点。这种求合力矢的几何作图法被称为力多边形法。
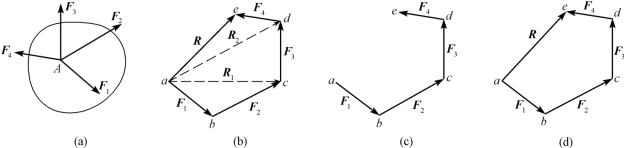
图2-2
上述方法可以推广到包含n个力的平面汇交力系中，得出结论为平面汇交力系的合力矢量等于力系中各力的矢量和，即
(https://www.chuimin.cn)
由此可见，合力的作用线通过各力的汇交点。
值得注意的是，作力多边形时，改变各力的顺序，可得不同形状的力多边形，但合力矢量的大小和方向并不改变。
【例2-1】 在拉环上套有在同一平面上的三根绳索，各绳的拉力分别为F1＝100N、F2＝150N、F3＝75N，各力的方向如图2-3（a）所示，试用几何法求三个力的合力。
【解】 拉力F1、F2、F3的作用力汇交于O点，构成平面汇交力系。选定比例，按力多边形法则依次画出F1、F2、F3，如图2-3（b）所示，连接AD，则矢量AD⇀代表合力R，依比例尺量得：
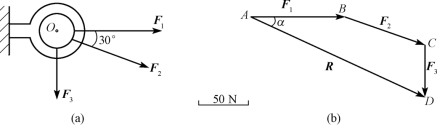
图2-3
相关文章
- 详细阅读
-
用几何法合成力系详细阅读
矢量关系式为或简写为若力系中各力的作用线位于同一条直线上，在这种特殊情况下，力多边形变成一条直线，合力为需要指出的是，利用几何法对力系进行合成，对于平面汇交力系，并不要求力系中各分力的作用点位于同一点，因为根据力的可传性原理，只要它们的作用线汇交于同一点即可。另外，几何法只适用于平面汇交力系，而对于空间汇交力系来说，由于作图不方便，用几何法求解是不适宜的。......
2025-09-29
-
建筑力学研究任务和内容，建筑力学第3版详细阅读
建筑力学的任务是研究结构的几何组成规律，以及在荷载作用下结构和构件的强度、刚度和稳定性问题。具体来说，建筑力学将讨论下列几个方面的内容：力系的简化和力系平衡问题。......
2025-09-30
-
常见约束及反力第3版建筑力学详细阅读
由于约束的类型不同，约束反力的作用方式也各不相同。下面介绍在工程中常见的几种约束类型及其约束反力的特性。（一）柔索约束由柔软且不计自重的绳索、链条等构成的约束称为柔索约束。所以，柔索的约束反力通过接触点，沿柔索中心线而背离所约束的物体，通常用符号T表示。物体A所受的约束反力T如图1-9所示。约束反力XA、YA对应于约束限制移动的位移；约束反力偶mA对应于约束限制转动的位移。......
2025-09-30
- 详细阅读
-
建筑力学第3版：荷载分类及计算详细阅读
2）活荷载是指在施工或建成后使用期间可能作用在结构上的可变荷载。如果分布荷载在一定的范围内连续作用且其大小在各处都相同，这种荷载称为均布荷载。例如，上面所述梁的自重按每米长度均匀分布，称为线均布荷载；又如上面所述的楼面荷载，按每单位面积均匀分布，称为面均布荷载。静力荷载的特点是该荷载作用在结构上时，不会引起结构振动。......
2025-09-30
-
建筑力学（第3版）-结构的计算简图详细阅读
在选取其计算简图时，可根据实际构造和约束情况进行。在计算简图中，通常可将结点分为铰结点和刚结点两种。事实上，结构在荷载作用下，杆件之间所产生的转动也相当小，所以，该结点应视为铰结点。因而，刚结点对杆端有阻止相对转动的约束力存在，既除产生杆端轴力和剪力外，还引起杆端弯矩。计算时这种结点应视为刚结点，其计算简图如图1-23所示。......
2025-09-30
-
平面立体截交线探究详细阅读
截切立体的平面称为截平面，截平面与立体表面的交线称为截交线，截交线所围成的平面图形称为截断面。求平面立体的截交线时，首先应确定平面立体的原始形状，进而分析其与投影面的相对位置；再分析截平面相对投影面和平面立体的位置，明确截交线的形状和投影特性，如积聚性、类似性等。分析截平面P与正四棱锥的四个侧棱面均相交，所以截交线为四边形。......
2025-09-29
相关推荐