图4.1成本预测的基本程序1)准备阶段准备阶段包括确立预测目标、收集资料、选择预测方法3 个步骤。3)提交预测报告阶段该阶段主要包括提出报告和追踪反馈两个步骤:①提出预测报告。预测结果得到确认后,便可提出预测报告。预测报告中至少包括预测结论及建议两项内容。......
2023-08-24
定量预测也称统计预测,它是根据已掌握的比较完备的历史统计数据,运用一定的数学方法进行科学的加工整理,借以揭示有关变量之间的规律性联系,用来预计和推测未来发展变化情况的一类预测方法。
1)时间序列法
时间序列法是将某种统计指标的数值,按时间先后顺序排列起来,并对其时间序列进行加工整理和分析,利用数列所反映出来的客观变动过程、发展趋势和发展速度,进行外推和延伸,借以预测今后可能达到的水平。 其主要可分为平均值法、移动平均值法、指数平滑法和季节指数法等。
(1)平均值法
平均值法是在算术平均值的基础上发展起来的一种简单的预测方法。 它适用于时间序列主要表现为随机变动时的预测。 根据平均值的计算方法不同可分为算术平均值、几何平均值和加权平均值法。
①算术平均值法
它是将历史数据对预测值的影响作用等同看待,采用简单算术平均值法计算预测值。 其计算公式为:

式中 Mi+1——第i+1 期的预测值;
Di——第i 期的实际值;
n——资料期数。
②加权平均值法
这种方法是在算术平均值的基础上,对所用资料按远近期不同分别给予不同权数(近期数据更能反映下期趋势,故其权数较大),然后以近期数据的加权平均数作为下期的预测值。 其计算公式为:
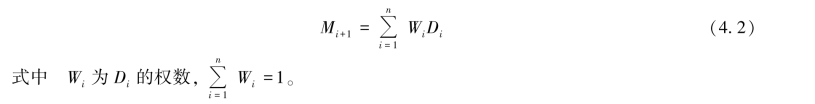
其余符号意义同前。
③几何平均值法
对于长期预测来说,为了反映时间序列的变动速度,可以采用几何平均值。
设Xi 为已知数据,i=1,2,…,n,则n 个计划内总体发展速度为V,每一年计划期的平均发展速度为ˉV,则有:V =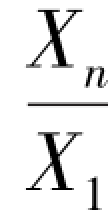
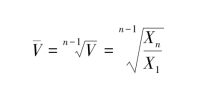
![]()
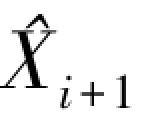 即为第i+1 计划期的预测值。
即为第i+1 计划期的预测值。
显然,这是把Xi 系列看成是平均的几何递增,这种方法对i+1 计划期数量预测结果远优于算术平均值法。
【例4.1】某工程项目前10 个月完成的预制构件数量见表4.1,试采用平均值法预测第11个月的预制构件数量。
表4.1 预制构件数量 单位:件

解:(1)采用算术平均值法预测
![]()
(2)采用加权平均值法预测
前5 个月权重系数取0.06,后5 个月权重系数取0.14,则:
M11=0.06×(10+15+8+20+10)+0.14×(16+18+20+22+24)=17.6(件)
(3)采用几何平均值法预测

(2)移动平均值法
由于实际数据序列既受偶然因素的作用而产生随机变动,也有反映发展规律的倾向性或周期性变动。 因此,如何消除或减少随机变动的影响,从数据模式中找出规律性变化的特征和趋势,是时间序列预测方法所要解决的技术问题。 移动平均值法是解决这类问题的方法之一。
①一次移动平均值法
一次移动平均值法的基本思路是,每次取一定数量周期的数据平均,按时间次序逐次推进。每推进一个周期,舍去前一个周期的数据,增加一个新周期的数据,再进行平均。 计算公式为:

式中 t——周期序列号;
M(1)t ——第t 周期的一次移动平均数;
Y——第t 周期的实际值;
N——计算移动平均数所选定的数据个数。
移动平均值法通过N 个数据移动平均值可以削弱数据随机变动的影响,起到平滑数据的作用,在一定程度上反映了时间序列的变化趋势。 因此,在计算移动平均值时,N 值的选择是一个关键,N 越大,平滑作用越强,对新数据的反映越迟钝,反之则相反。 同时计算出的移动平均数总是落后于实际数据,存在滞后偏差,N 越大,滞后偏差越大。
一般可用最近时间的一次移动平均数作为下一周期的预测值,即:
![]()
②二次移动平均值法
二次移动平均值法适用于时间序列具有线性趋势的场合,它不是用二次移动平均数直接进行预测,而是建立线性预测模型,然后用模型预测。 计算公式为:

式中 t——周期序列号;
 ——第t 周期的一次移动平均数;
——第t 周期的一次移动平均数;
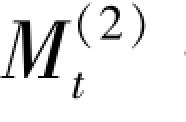 ——第t 周期的二次移动平均数;
——第t 周期的二次移动平均数;
N——计算移动平均数所选定的数据个数。
利用二次移动平均值法进行预测的基本公式是:

式中 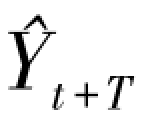 ——代表t+T 周期的预测值;
——代表t+T 周期的预测值;
at,bt——代表平滑系数。
【例4.2】数据同例4.1,试采用移动平均值法预测第11 个月的预制构件数量。
解:(1)采用一次移动平均值法预测
取N=3,计算一次移动平均值M(1)
t ,结果如表4.2 所列。
表4.2 一次移动平均值 单位:件

![]()
(2)采用二次移动平均值法预测
在一次移动平均值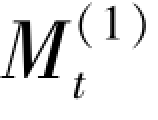 (N =3) 的基础上,计算二次移动平均值
(N =3) 的基础上,计算二次移动平均值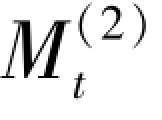 ,结果如表4.3 所列。
,结果如表4.3 所列。
表4.3 二次移动平均值

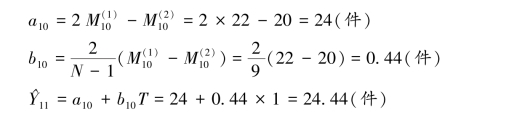
(3)指数平滑法
指数平滑法是在加权平均值法的基础是发展起来的。
①一次指数平滑法
指数平滑又称指数修匀。 可以消除时间序列的偶然性变动,进而寻找预测对象的变化特征和趋势。 一次指数平滑法适用于实际数据序列以随机变动为主的场合。 一次指数平滑值的计算公式:
![]()
式中  ——第t 周期的一次指数平滑值;
——第t 周期的一次指数平滑值;
yt——第t 周期的实际值;
a——平滑系数(0﹤a﹤1)。
实际值yt、yt-1 的权数分别为a、a(1-a)、a(1-a)2…距现时刻越远的数据,其权系数越小。指数平滑法就是用平滑系数来实现不同时间的数据的非等权处理。 因为权系数是指数几何级数,指数平滑法也因此得名。
式(4.8)略加变换,得:
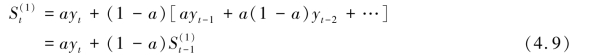
式中  为第t-1 周期的一次指数平滑值。
为第t-1 周期的一次指数平滑值。
一次指数平滑法是以最近周期的一次指数平滑值作为下一个周期的预测值的。 即:

上式可改写成:
![]()
式(4.10)、(4.11)均称为一次平滑预测模型。
计算指数平滑值必须先估计一个初始值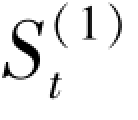 。 当实际数据较多(﹥50)时,取
。 当实际数据较多(﹥50)时,取 = Y1,如果数据较少(≤20),
= Y1,如果数据较少(≤20),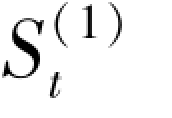 =(Y1+Y2+Y3)/3。
=(Y1+Y2+Y3)/3。
平滑系数a 的选择是关键,一般认为时间序列的长期趋势比较稳定,取a=0.05 ~0.20;如时间序列具有迅速明显的变动倾向时,取a=0.3 ~0.7,使时间序列中最近数据的作用能更多地反映在预测值中。
②二次指数平滑法
如实际数列具有较明显的线性增长倾向,则不宜用一次指数平滑法,因为滞后偏差将使预计值偏低。 此时,通常可用二次指数平滑法建立线性预测模型,然后再用模型预测。 计算公式为:
![]()
式中 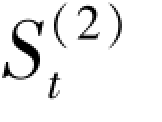 ——第t 周期的二次指数平滑值;
——第t 周期的二次指数平滑值;
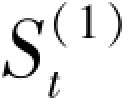 ——第t 周期的一次指数平滑值;
——第t 周期的一次指数平滑值;
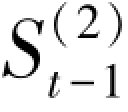 ——第t-1 周期的二次指数平滑值;
——第t-1 周期的二次指数平滑值;
a ——平滑系数。
二次指数平滑值并不直接用于预测,根据滞后偏差的演变规律建立线性预测模型。 即:
![]()
式中 t——目前的周期序号;
T——预测超前周期数;
at——线性模型的截距;
bt——线性模型的斜率;
Yt+T——第t+T 周期的预测值。
其中at 和bt 的计算公式为:

③三次指数平滑法
如果实际数据序列具有非线性增长倾向,则一次、二次指数平滑法都不适用了。 此时应采用三次指数平滑法建立非线性预测模型,再用模型进行预测。 计算公式为:

a——平滑系数。
三次指数平滑法建立的非线性预测模型为:
![]()
式中 t——目前的周期序列号;
T——预测超前周期数;
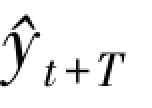 ——第t+T 周期的预测值。
——第t+T 周期的预测值。
其中模型系数at、bt、ct 的计算公式为:

【例4.3】数据同例4.1,试采用指数平滑法预测第11 个月的预制构件数量。
解:(1)采用一次指数平滑法预测
取平滑系数a=0.5,计算一次指数平滑值如下:
![]()
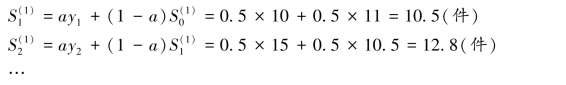
依次类推,其余计算结果如表4.4 所示。
表4.4 一次指数平滑法预测 单位:件

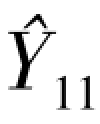 =
= 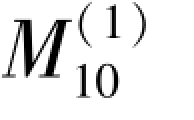 = 22(件)
= 22(件)
(2)采用二次指数平滑法预测
在一次平滑指数值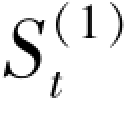 (a = 0.5) 的基础上计算
(a = 0.5) 的基础上计算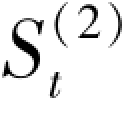 ,结果如表4.5 所列。
,结果如表4.5 所列。
表4.5 二次指数平滑法预测 单位:件

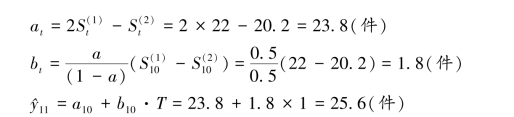
(3)采用三次指数平滑法预测
在二次平滑指数值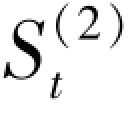 (a = 0.5) 的基础上计算
(a = 0.5) 的基础上计算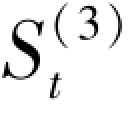 ,结果如表4.6 所列。
,结果如表4.6 所列。
表4.6 三次指数平滑法预测 单位:件

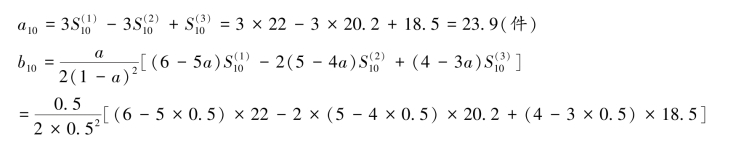
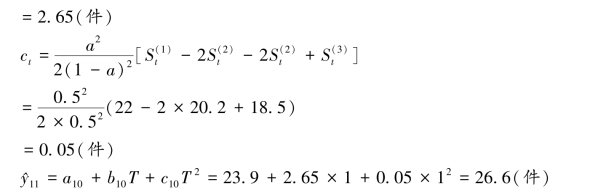
(4)季节指数法
工程项目的施工一般都是露天作业,受自然气候条件影响大,生产成果经常会出现季节性变动的现象。 为了适应生产的要求,搞好均衡生产,有必要掌握这种季节性变动的规律。
季节指数预测法的基本思路:先建立描述整个时间序列总体发展趋势的数学方程,再考虑季节变动对预测对象的影响,计算出季节指数,最后将两者综合而得到能够描述总体发展趋势与季节性变动的预测模型,并用于预测。 季节指数预测模型为:
![]()
式中 ^yt ——第t 周期的预测值;
y′——反映总体发展趋势的数学方程;
Fk——季节周期中第k 周期的季节指数。
如果时间序列具有线性增长趋势,则y′为一直线方程,即:
![]()
【例4.4】某工程项目2015、2016 和2017 年各月实际完成的工作量见表4.7 所列,据此来估计2018 年各月预计完成的工作量。
表4.7 各月实际完成的工程量
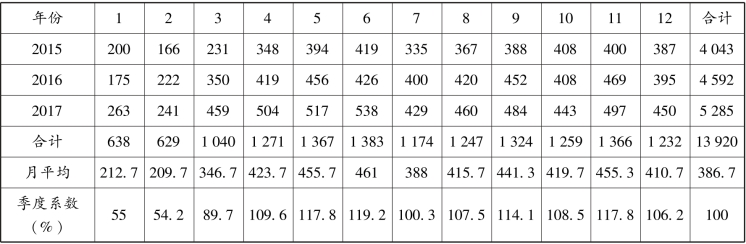
解:(1)根据历史数据,分析变动性质
从表4.7 中可以看出,实际完成的工作量总的来说是呈递增趋势,并且伴随着以年为周期的季节性变动。
(2)确定季节系数
为确定季节系数,应分别求出月平均值与总平均值。 季节系数可由下式确定:
![]()
季节系数计算结果见表4.7 中第7 行。
(3)确定长期变动趋势
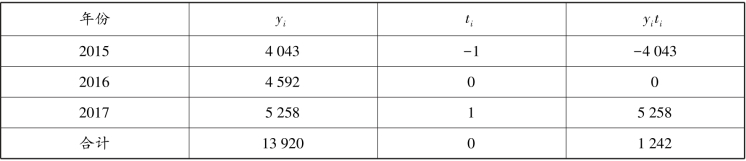
本例中的长期变动趋势为线性趋势,故选择一元线性回归方程y=a+bt 作为趋势模型,模型参数a、b 可采用最小二乘法确定。 由于本例历史数据较少(n=3),采用算术平均值法确定a、b,计算过程如表4.8 所列。
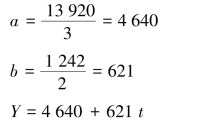
2018 年相应的t 值为2,故2018 年预计完成的工作量为:
![]()
表4.8 计算过程
(4)计算各月预测值
各月预测值可按下式确定:

计算结果列于表4.9。
表4.9 计算各月预测值

2)回归分析法
回归分析法是以相关原理为基础的预测方法。 基本思路是分析研究预测对象与有关因素的相互联系,用适当的回归预测模型表达出来,然后再根据数学模型预测其未来状况。
回归分析是处理变量之间相关关系的一种数理统计方法。 在回归预测中,把预测对象作为因变量,把相关因素称为自变量。 一个自变量的称为一元回归,多个自变量的称为多元回归。如果因变量与自变量的统计规律呈线性关系,称为线性回归;呈曲线关系的称为非线性回归。
(1)一元线性回归
当两个变量之间存在线性关系,即一个变量的增加或减少相对于另一个变量的增、减来说成一定比例时,根据自变量去预测因变量的方法,称为一元线性回归法。 此法的基本步骤如下:
①根据历史数据绘出散点图。 若图中各数据点的分布呈线性趋势,即大体沿一条直线分布,说明可以应用一元线性回归法进行预测。
②建立模型。 一元线性回归方程模型是:
![]()
③参数估计。 根据数理统计中的最小二乘法,可按下式分别求出回归系数a、b 值。

式中 Xi、Yi ——分别为自变量、因变量的历史数据;
 ——分别为自变量、因变量的平均值。
——分别为自变量、因变量的平均值。
④相关性检验。 任何一组数据都可求得回归直线方程,但y 与X 是否确实有线性相关关系,须加以检验,检验可以采用相关系数判断。 相关系数是描述两个变量线性关系密切程度的数量指标,其计算公式为:
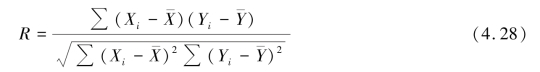
当Ra ≤R 时,Y 与X 存在显著的线性关系;当Ra ﹥R 时,Y 与X 不存在显著的线性关系。
Ra 可以根据显著性水平a 查相关关系检验表得到,它表示对线性关系密切程度的最低要求临界值。
⑤应用回归模型进行预测。
(2)一元曲线回归
在实际应用中,一个自变量对因变量的影响,并不都呈线性关系,而需要采用一元曲线回归。 对这类问题预测的关键是确定自变量与因变量之间的函数关系,为此,先将历史数据在图上标画出来,观察数据点的分布趋势和形状,或者通过数据分析确定出变化规律,然后再拟合成近似的曲线方程。 由于非线性问题一般比较复杂,在确定函数方程后,通过变换将其转换成线性函数来求解。
常用的一元曲线回归预测有二次曲线、指数曲线和双曲线等。
①一次曲线回归预测
一元二次回归方程的基本公式是:
![]()
式中 y ——因变量;
X1——自变量;
a,b1,b2——非线性回归系数。
求解非线性回归系数的方法是把非线性回归转化为线性回归。
假设X2 =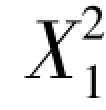 ,带入式(4.29),即可得:
,带入式(4.29),即可得:
![]()
这样,就把一元二次回归方程变成二元一次回归方程。 我们只要把X2 =X21 当作原始数据,运用二元线性回归预测法,求出回归系数a,b1,b2,从而建立一元非线性回归预测模型,就可以进行预测了。
②指数曲线回归预测
指数曲线的数学模型为幂函数形式,其公式是:
![]()
将等式两边取对数,即可化非线性回归为线性回归。
![]()
设y′ = lg y,a′ = lg a,X′ = lg X,则:
![]()
然后,运用一元线性回归预测法求出y′,再查反对数表,即可求得未来预测值y。
③双曲线回归预测
双曲线的数学模型为双曲线函数形式,其公式为:
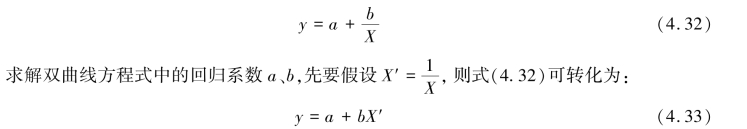
根据最小二乘法,可以导出两个标准方程式,求得回归系数a、b。
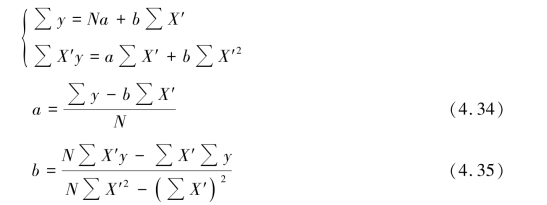
然后,建立回归预测模型y = a + bX′,即可进行预测。
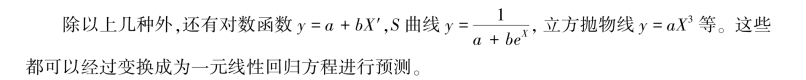
(3)多元回归预测
多元线性回归分析首先是因素选择问题。 对于任一预测对象y,影响预测对象的因素可能有N 个,关键在于选择主要的、起决定作用的因素。 选择是通过检验因素间的相关性,即相关系数r 来进行的。
下面以二元线性回归说明预测模型的建立。 二元线性回归预测是分析一个因变量和两个自变量之间呈线性关系的一种预测方法。 基本公式为:
![]()
式中 X1,X2——自变量;
a,b1,b2——回归系数。
利用最小二乘法可以求得3 个标准方程:
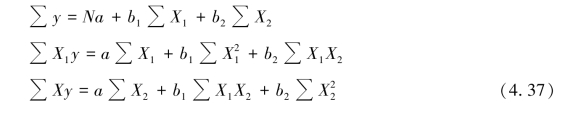
解此方程组,可得a、b1、b2,或利用回归系数求解公式,即:

求得a、b1、b2 后,代入y = a + b1X1 + b2X2,即可进行预测。
【例4.5】已知某项目施工产值与成本的历史数据如表4.10 所列。 预计下一年度施工产值为700 万元,试预测下年度总成本。
表4.10 施工产值与成本的历史数据

解:由于历史数据呈线性增长趋势,选用一元一次回归模型预测。
(1)计算模型参数
数据的计算过程如表4.11 所列。
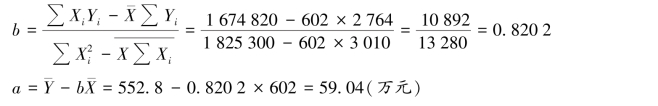
表4.11 计算过程
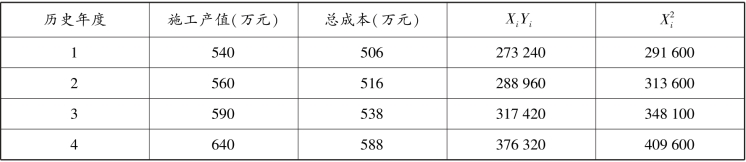
续表

(2)预测下一年度总成本
Y = a + bX = 59.04 + 0.820 2 × 700 = 633.18(万元)
3)高低点法
在一定的生产规模下,工程项目各期成本费用中有一部分是相对固定的,即不会随着产量或工作量的变动而变动,如固定资产折旧费、管理人员工资费用、水电费等,而另一部分则随着产量或工作量的变动而变动,如直接材料、直接人工费用等。 因此,固定成本、变动成本和工作量之间具有下列线性关系:
![]()
高低点法就是依据上述关系,选取某一历史时期内的成本数据,以最高点工作量的成本与最低点工作量的成本的差数,除以最高与最低工作量的差数,以确定单位变动成本,进而预测报告期成本费用的方法。 预测公式如下:

式中 a——固定成本;
y1,Y2——分别为最高点和最低点成本;
x1,X2——分别为最高点和最低点产值。
【例4.6】某施工项目的合同价为190 000 万元。 试根据企业同类项目的产值与成本(见表4.12)进行总成本预测。
表4.12 同类项目产值与成本

解:(1)计算模型参数
b = (157 000 - 110 000)(172 000 - 120 000)= 0.903 8
a = 157 000 - 0.903 8 × 172 000 = 1 546.4
由此得出预测模型:Y = 1 546.4 + 0.903 8X
(2)预测总成本
该预测项目的总成本为:
Y = 1 546.4 + 0.903 8 × 190 000 = 173 268.4(万元)
4)本量利分析法
成本、业务量、利润三者关系的分析,简称本量利分析。 本量利是在成本分析的基础上,通过对成本、业务量和利润三者之间的依存关系建立数学模型和公式,从而进行成本预测的方法。
(1)固定成本和变动成本的划分
施工项目要取得收入,必有相应的耗费,而且收入必须大于耗费才能盈利。 施工项目的成本支出,按其数量与产量变动的内在联系,通常可以划分为变动成本和固定成本两类。
①固定成本,是指成本总额在一定时期和一定产量范围年内不受产量影响的成本。 其特点是总额不随产量变化而变化,但单位额却随产量的增加而减少(即固定成本利润率的提高)。施工成本中的施工现场管理人员工资和办公费、临时设施费等属于固定成本。
②变动成本,是指成本总额在一定时期和一定产量范围内随着产量的变动而成正比例变动的成本。 其特点是总额随产量变化而正比例变化,单位额保持不变。 施工成本中的人工、材料以及机械设备中的变动费用等均属于变动成本。
除了固定成本和变动成本外,还有一种介于固定成本和变动成本之间的费用,它可以通过一定的方法分解为固定成本和变动成本两部分。 因此,我们可以认为施工的全部费用最终可以分解为固定成本和变动成本两种类型。
(2)本量利分析的基本公式
将成本分解成固定成本和变动成本两部分之后,再把收入和利润加进来,成本、产量和利润的关系就可以统一于一个数字模型,即本量利公式:

(3)保本点的预算
保本点又称盈亏平衡点,是指施工项目在这个水平上,总收入与总成本相等,既无利润,也不亏损,刚好够本。 因此,保本点这个指标能够明确指出施工项目或分项工程在什么样的收入水平上,才能维持不赔不赚,并能预知在保本点以上,每收入一万元能够降低多少成本,获得多少利润。
保本点的测算是以变动成本率与边际利润率为计算基础。
①变动成本率与边际利润率
变动成本率是指变动成本额占工程预算成本的比例。 用公式表示如下:
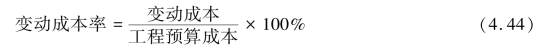
工程预算成本减去变动成本后的余额称为边际利润,它是用来补偿固定成本和为项目提供施工利润。 用公式表示如下:
![]()
如果边际利润与固定成本相等,则项目不盈不亏;若大于固定成本,则为盈利;反之,则为亏损。 边际利润的意义在于:它表明了能为项目提供施工利润的能力。 所以边际利润又称边际贡献、贡献毛利或创利额。 边际利润的多少对获取施工利润具有重要作用。
边际利润与工程预算成本的比值为边际利润率。 用公式表示如下:
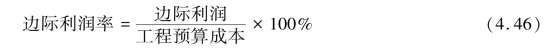
边际利润率与变动成本率之间有着密切的联系,属于互补性质,变动成本率越高,边际利润率越低,盈利能力越小;反之,变动成本率越低,边际利润率越高,盈利能力越强。 边际利润率与变动成本率的关系用公式表示如下:
![]()
②保本点
因为:

所以

当利润为零时的成本即为保本点,式(4.50)可变为:
![]()
将式(4.49)代入式(4.51),可得保本点的另一表达:
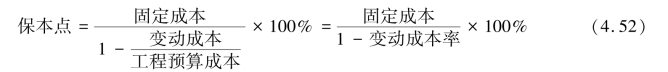
(4)本量利分析法预测降低成本目标
工程项目的降低成本目标,也就是计划成本降低率,由下式计算:
![]()
在工程项目已中标,签订合同后,工程预算成本是可知的。 所以要确定计划成本降低率,就应预测工程目标成本。
预测工程目标成本时,应以历史或上一年度的实际成本资料作为测算的主要依据,按客观存在的成本与产量的依存关系,把成本分为固定成本和变动成本两大类,再分析研究历史或上年度固定成本和变动成本的情况,结合工程项目计划期的实际情况及要采取的技术组织措施,确定计划年度固定成本和变动成本水平,并预测计划期在一定产量下的最优目标成本。
预测的步骤和方法如下:
①将历史或上年度的实际成本划分为固定成本和变动成本。
②计算历史或上年度变动成本率、边际利润和边际利润率。
③假定计划年度固定成本与历史或上年度相同(实际中因客观和主观的某些原因可能有所升降),预测计划年度的保本点。 通过保本点的预测可以预知项目必须完成的预算工作量。
④在工程任务确定的条件下,预测计划年度目标成本和计划成本降低率。

【例4.7】某工程项目上年度成本报表中,预算成本3 700 万元,实际成本3 480 万元。 在实际成本中,划为固定成本的为955 万元,变动成本为2 525 万元。 该项目计划年度已确定工程预算成本为3 800 万元,固定成本基本和上年度相同,试预测本年度保本点和目标成本。
解:(1)计算上年度变动成本率、边际利润、边际利润率

上式表明,计划年度必须完成预算成本3 007 万元才能保本,不亏损。 如果超过3 007 万元就能盈利,每超过100 万元,盈利31.76 万元。
(3)预测计划年度目标成本和计划成本降低率
目标成本= 955 + 3 800 × 68.24% = 3 548(万元)
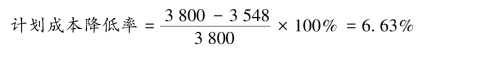
有关道路桥梁工程概预算(第2版)的文章

图4.1成本预测的基本程序1)准备阶段准备阶段包括确立预测目标、收集资料、选择预测方法3 个步骤。3)提交预测报告阶段该阶段主要包括提出报告和追踪反馈两个步骤:①提出预测报告。预测结果得到确认后,便可提出预测报告。预测报告中至少包括预测结论及建议两项内容。......
2023-08-24

某高速公路的一段,路基土方挖方土质为普通土,平均运距30 m 的有1 000 000 m3,平均运距50 m 的有1 000 000 m3,平均运距200 m 的有1 000 000 m3,平均运距3 000 m 的有1 000 000 m3。提出不同机械施工方式的预算定额工程细目名称、定额表号及定额直接费。......
2023-08-24

工程概预算是决定工程结构物设计价值的造价文件,是基本建设管理工作中的重要环节。概预算文件编制质量的好坏,对国家基本建设资金是否能正确合理地使用有重大的影响。首先,概预算有货币的指标体系。会计的有关科目应和概预算一致,才能对照工程概预算各费用项目,进行成本分析。同时,通过对在建项目的概预算完成情况的统计,可以及时了解工程的进度。......
2023-08-24

我国公路工程定额具有科学性、系统性、统一性、权威性、相对稳定性的特点。在社会主义市场经济的条件下,定额必然牵涉各有关方面的经济关系和利益关系。5)定额的相对稳定性定额所反映的是一定时期内的施工技术和先进工艺的水平,所以表现为一定的稳定性。......
2023-08-24

专项费用包括施工场地建设费和安全生产费。④工地试验室所发生的属于固定资产的试验设备和仪器等折旧、维修或租赁费用。⑥文明施工、职工健康生活的费用。施工场地计费基数为定额建筑安装工程费减去专项费用。安全生产费按建筑安装工程费乘以安全生产费费率计算,费率按不少于1.5%计取。......
2023-08-24

生产准备费是指为保证新建、改扩建项目交付使用后满足正常的运行、管理发生的工器具购置、办公和生活用家具购置、生产人员培训、应急保通设备购置等费用。应急保通设备购置费应急保通设备购置费,指新建、改扩建工程项目,为满足初期正常营运,购置保障抢修保通、应急处置,且构成固定资产的设备所需的费用。该费用由设计单位列出计划购置清单,计算方法同设备购置费。......
2023-08-24

概、预算文件由封面及目录,概、预算编制说明和全部概、预算计算表格组成。图2.2概预算费用组成②采用的定额、费用标准,人工、材料、机械台班单价的计算依据或来源,补充定额及编制依据的详细说明。概、预算表格概预算文件的主要内容和组成部分是概预算表格,它实际上是由一套规定的表格所组成。......
2023-08-24

时间定额与产量定额互为倒数。2)材料消耗定额材料消耗定额简称材料定额,是指在节约和合理使用材料的条件下,完成一定合格产品所需消耗材料的数量标准。4)机械台班费用定额机械台班费用定额是以机械的一个台班为单位,规定其所消耗的工时、燃料及费用等数量标准并可折算为货币形式表现的定额。......
2023-08-24
相关推荐