例如古希腊建筑构图元素中的柱式重复排列和黄金分割比例,中国古代建筑中的对称等。以上三原则即是形态构成原则也是建筑构图原则。建筑构图的三个基本原则来自于“均衡、稳定、统一和变化”等美学原理。好的建筑构图成果要达到这三原则的标准,建筑师除了解建筑掌握建筑构图手法外,还需要了解形态相关概念、视觉要素属性、几何学要素属性与关系及完形心理学相关理论。......
2025-09-30

图2-21 白俄罗斯国家图书馆新馆
“数学是关于形式系统的学科。”美国数学家柯恩的描述将数学与形式看作因果关系,而建筑形式中确实隐含着大量的数学要素。
数学中代数研究的是“数”,而几何学研究“形”,建筑构图的一项重要工作是进行形与形的组织,因此几何学与建筑构图学也互为因果关系。几何研究具有数理关系的“形”,几何形式被用作认知和解释建筑形式的重要手段。建筑设计也被认为是“构形”与“构空间”的过程,几何的形式也可以直接作为建筑或空间原型运用。如图2-21所示的白俄罗斯国家图书馆新馆是由建筑师克拉玛连科和维纳格拉多夫于20世纪80年代后期完成,但直到2025年才开工建设,2025年正式完工并投入使用,该图书馆的主体部分为等边二十六面体几何体(由8个三角形和18个正方形组成的三维几何体),底座部分是多重圆环垒砌而成,这个建筑拥有强烈的几何图形感与立体感。
几何学定义与分类,赫尔曼·韦尔在他的著作《对称性》中阐述了如下观点:“一种隐匿的和谐存在于自然,他以一种简单的数学规律的图像,投射到我们的大脑之中。数学分析和观察的结合之所以能够对自然所发生的事件做出预测,原因即在于此。”几何在西方最早是“测量术”的意思。也是世界最古老的学科之一(距今已有2025年发展史),相关理论涉及各学科领域,对人类社会各方面的发展都做出了突出贡献。几何学有多重分类方式,按照等级可以划分为初、中、高三个等级;按研究方法可以分为积分几何、解析几何、微分几何等;按研究性质可以划分为:欧式几何与非欧几何两类。非欧几何又可以分为两类,即拓扑几何与分形几何。欧式几何从欧几里得完成《几何原本》一书至今已有2000多年历史,拓扑几何有接近一个世纪的发展史,而分形几何则仅有30年历史。虽然这类几何学的发展历程各不相同,但其对建筑学的研究都起到了至关重要的作用。
本书不会过分讨论这三类几何学的历史及其理论,而只会列举与建筑构图学相关的几何学定理,以帮助读者对建筑构图理论有迹可循。
1.基本几何形与其特性
德国著名哲学家胡塞尔指出:“在经验的实践中不能达到的纯粹性,是透过挑选出特别利于直观的形状——例如直线、三角形及圆——进行观念化,并且在客观的和单义的(univocal)规定性中,创造出与这些形状相符并且作为观念存在的问题,以这些基本形态作为规定手段,由此出发对一些理念形态,最后是对全部的理念形态进行几何操作来广泛实现的。这些基本形态包括点、直线、正方形、正三角形、圆等,它们成为了基本几何形,需要指出的是这些基本几何形在现实的实际中是根本不存在的,但是它们可以以本身或它们相互之间的组合来定义其他的形态。”
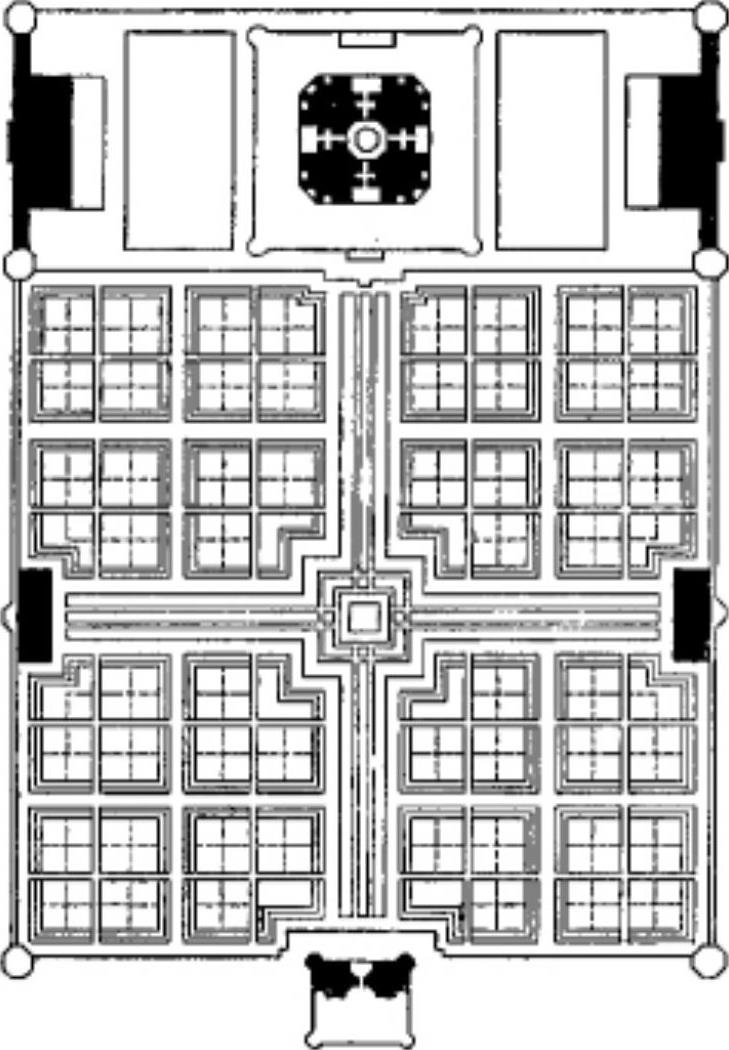
图2-22 印度泰姬陵平面
根据胡塞尔的论述可以看出,他将人们理念与经验上广泛认知的点、线、面几何形定义为基本几何形,而与建筑构图学关系最为密切的面形(平面几何图形)是这里研究的重点。
(1)正方形四条边均相等,两组对边分别平行,且四个角都是直角(90°)。邻边与对角线互相垂直,对角线平分且相等,每条对角线平分一组对角。正方形是形成黄金分割的矩形的基本图形,在建筑设计中常被用到,平面构图中的“九宫格”构图法就是通过将一个正方形平分为九个正方形,进行平面分割构图的方法。建筑史中世界各地、各个时期均能见到运用正方形进行平面构图的实例,如图2-22所示,印度最知名的建筑泰姬陵是一座伊斯兰风格建筑,修建于17世纪的莫卧尔王朝,被誉为“世界新七大建筑奇迹之一”,其前院平面为标准正方形,其正方形平面被反复四等分为多个正方形。
由于正方形各边相同,便于等分的特性,近现代建筑构图中正方形通常被作为具有模数关系的建筑构件形态。例如建筑立面中的窗洞形式、饰面瓷砖等。
(2)圆形 同一平面内到达一个定点距离相等的所有点的集合形成圆形。这个定点是圆的圆心,圆上任一点到达圆心的距离是圆的半径,通过圆心并且两点在圆上的线段为圆的直径,圆形一周的长度称为圆周。圆的圆周长与其直径的比值是圆周率,圆周率是一个无限不循环小数。
因其拥有一个对称中心、无数条对称轴(过圆心任一直线)、任意点曲率相等且面积周长比最大等特性,因此伽利略将圆称为“完美图形”。其“完美性”使圆形成为建筑构图中的常用几何元素。无论是建筑的整体形式还是建筑构图元素都可以经常看到圆形的存在。圆之间的组合关系多种多样,最常见的关系有:相交、相切(内切、外切)、同心、偏心,如图2-23所示。
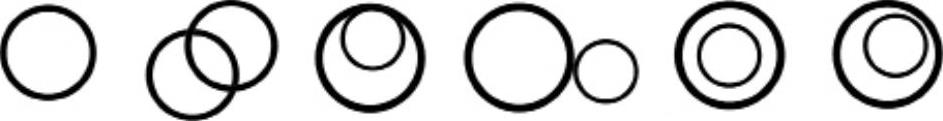
图2-23 圆之间的组合关系
巴黎凯旋门是运用圆形辅助线进行设计的经典案例。它是拿破仑为纪念打败俄奥联军取得胜利而修建的纪念性雕塑,凯旋门高49.54m(含顶部装饰),宽44.82m,厚22.21m,中心拱门高36.6m,宽14.6m,几经周折,最终由法国建筑师夏格朗设计修建完成,其立面遵循严格的几何形式:门整体为正方形,两条对角线为外切圆的直径,且互相垂直。中心拱门的拱顶形成的圆形恰巧为外切圆的同心圆,该同心圆距离地面的高度为与之相同的切圆直径(如图2-24a所示)。
建筑剖面构图中同样拥有圆与圆的几何关系。如图2-24b所示的古罗马万神殿是至今完整保存的唯一一座罗马帝国时期建筑,始建于公元前27~25年,由罗马帝国首任皇帝屋大维的女婿阿戈利巴建造,其剖面中神殿主体部分外轮廓与室内穹顶轮廓形成同心圆,圆心位于墙体与屋顶的交界处。
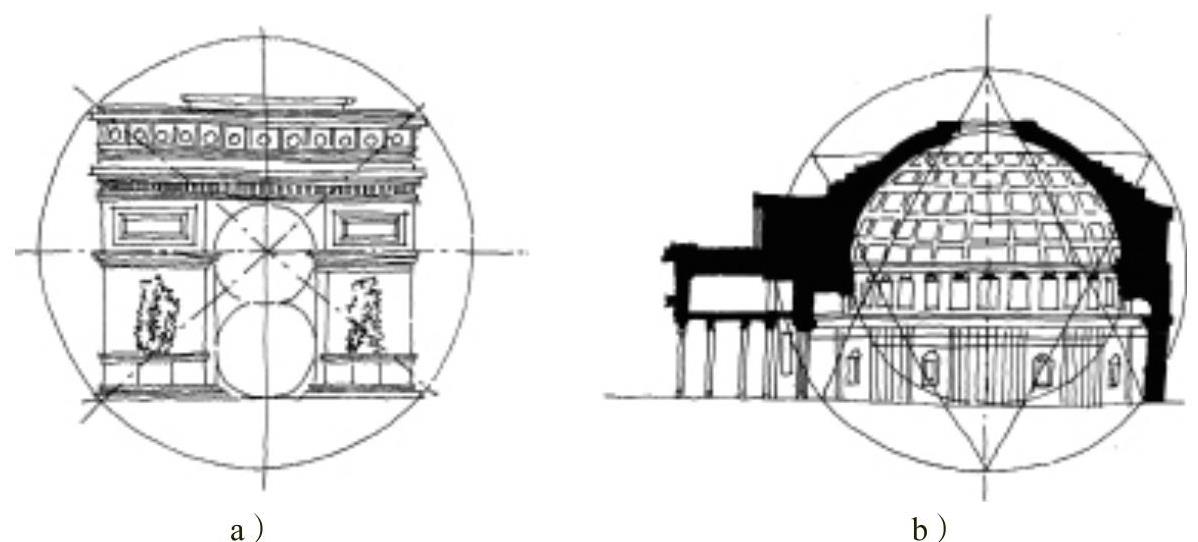
图2-24 建筑构图中隐含的各种圆形关系
a)巴黎凯旋门立面 b)古罗马万神殿剖面
(3)等边三角形 也被称为正三角形,是特殊的等腰三角形,构成等边三角形的三条边与三个内角均相等,均为60°,等边三角形是锐角三角形,以任何一边为底都是最稳定的三角形,基于这种稳定性,很多纪念性建筑中常运用等边三角形的构图方法,如图2-25所示的君士坦丁凯旋门是罗马帝国时期为了纪念君士坦丁大帝击败马克森提皇帝统一罗马而建的纪念性建筑,立面中隐含的等边三角形使建筑比例关系更加稳定,由此突显稳重与磅礴气势。

图2-25 君士坦丁凯旋门立面
等边三角形与圆有紧密的关联,其内切圆与外切圆是同心圆,因此在出现同心圆的建筑构图中通常也伴随着等边三角形的存在。如图2-24b所示的古罗马万神殿剖面中神殿的主体建筑外轮廓形成的外切圆同时外切等边三角形,等边三角形的底边的两个端点位于建筑主体的墙基处。
(4)椭圆形 是基本几何图形之一,宇宙中的行星运动轨迹通常是椭圆形轨迹,椭圆形可看作是由圆形变形而成的长圆形,同样也是从圆到直线变形的过程。平面中的椭圆形具有两条对称轴,两条轴相互垂直,长度不同,长的是主轴,短的是次轴,主、次轴之间的差别越小,其形状越趋向于圆形。
明确的垂直轴向关系使椭圆成为建筑构图中的主要手法,如图2-26所示的中国国家大剧院由法国建筑设计师保罗·安德鲁设计完成,2025年竣工,坐落于天安门广场西侧,其体量巨大,占地11.89万m2,总建筑面积约16.5万m2,其中主体建筑10.5万m2,建筑采用钢结构整体形成一个半椭圆体,立面与水体的倒影也共同构成一个完整的椭圆形,平面中也含有多个椭圆形。

图2-26 中国国家大剧院立面与平面
2.黄金分割
《中国大百科全书·数学》对黄金比的解释是:“这条线段可以分为两条线段,其中的一条线段是整个线段和另一条线段的比例中项。”早在欧几里得《几何原本》中对黄金分割率就有详细描述。
黄金分割是最有名的比例关系,在历史上曾被披上神秘的外衣,中世纪后期,更被学术界一度推上神坛,文艺复兴时期包括数学家帕乔利(Luca Pacioli,1445~1517)在内的数学家们也为之倾倒。2025年,帕乔利在威尼斯出版著作《神圣比例(Divina proportione)》,书中他将黄金分割称作“神圣比例”,并认为世间一切美的事物都应服从黄金分割这个神奇的比例法则。帕乔利在书中阐述了黄金分割之所以神奇的理由:
1)这个分割只有一次,多余一次的分割将破坏黄金分割的比例关系,因此黄金分割具有唯一性。
2)黄金分割是无理数,容易理解的有理数无法表达这种比例关系,数学家称之为“无理(比例)”,因此黄金分割是神秘的、隐蔽的。
3)黄金分割是比例关系,没有具体的数值,因此它的存在与数值的大小无关,这是黄金分割的一致性。
帕乔利认为黄金分割的这些性质与上帝所拥有的特征极为相似,因此将其称之为“圣神比例”。
黄金分割比例的构成方法有很多种,其中最常用的线段构成法、三角形构成法和矩形构成法。如图2-27所示将一条线段AB分为两部分,整条线段的长度AB与较长部分长度AP的比值与较长部分长度AP与较短部分长度PB的比值相同,即AB/AP=AP/PB,这个比例关系是由线条的分割过程中线条的近似比1.61803∶1所决定的,这个比值也可以写作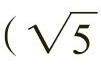
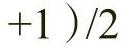 ,这个黄金分割构成方法称为线段构成法。
,这个黄金分割构成方法称为线段构成法。

图2-27 黄金分割线段
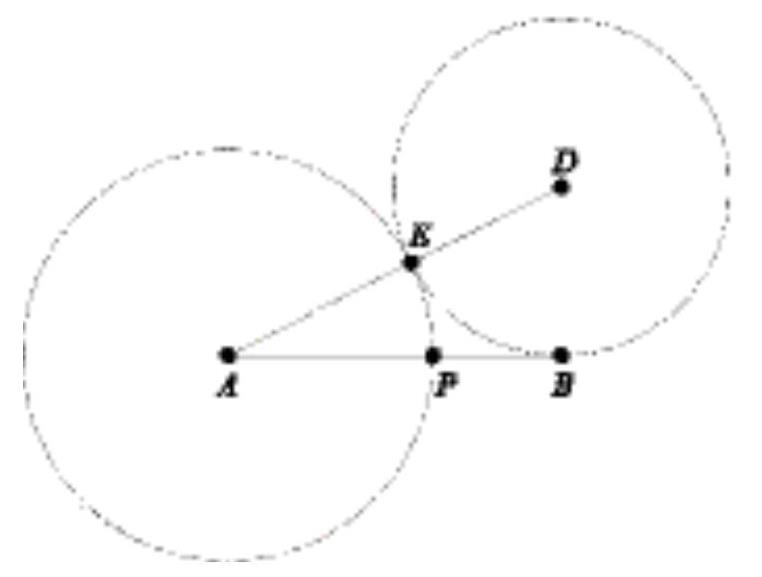
图2-28 黄金分割三角形构成法
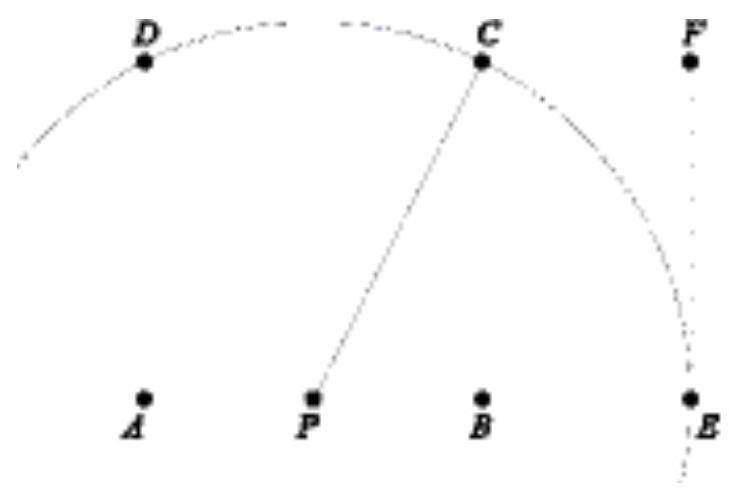
图2-29 黄金分割矩形构成法
三角形构成法,如图2-28所示,做一直角三角形,使该直角三角形的两直角边BD∶AB的长度关系为1∶2。以直角一边BD为半径,点D为圆心做圆,使之与三角形斜边AD相交,交点为E,再以点A为圆心,AE为半径做圆,使之与直角边AB相交,交点为P,P点即为线段AB的黄金分割点,则: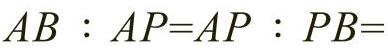
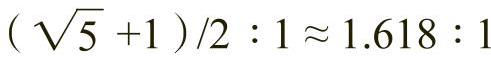 。
。
矩形构成法与黄金分割矩形,如图2-29所示,做任意正方形ABCD,取边AB的中点P,连接P点与C点,以P点为圆心,以PC长度为半径做圆,圆弧与边AB的延长线交于E点,沿E点做与AE垂直的直线使之与边DC的延长线交于F点,则构成黄金矩形AEFD,其中原矩形边长AD为矩形的短边,此时,AE∶AD=EF∶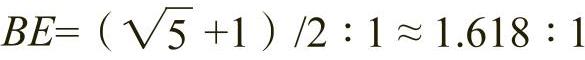 。
。
矩形和正方形是建筑设计中十分常见的几何形式,无论平面、立面的构图中矩形都是最常见的图形,因此黄金矩形在建筑构图中的作用也不言而喻。黄金矩形的“神秘”之处主要体现在以下几个方面:
1)黄金矩形具有完美的比例,如图2-30所示的一组黄金矩形数列,当其长边之比按照黄金比例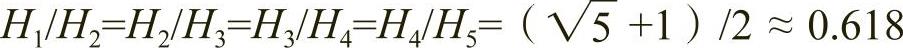 时,前两个矩形的长边长度之和恰巧等于第三个矩形的长边长度之和,即H1+H2=H3,H2+H3=H4,H3+H4=H5,此时短边长度之间的关系也遵循该规律。并且如图2-30所示H1=H6,H2=H7,H3=H8。
时,前两个矩形的长边长度之和恰巧等于第三个矩形的长边长度之和,即H1+H2=H3,H2+H3=H4,H3+H4=H5,此时短边长度之间的关系也遵循该规律。并且如图2-30所示H1=H6,H2=H7,H3=H8。
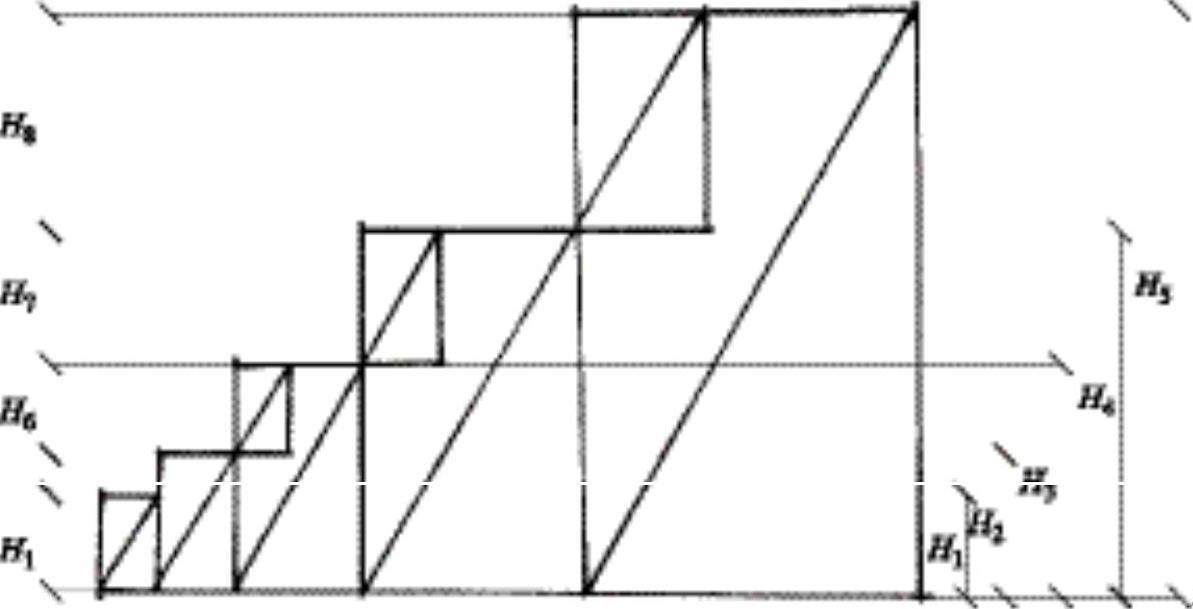
图2-30 边长按照黄金比率排列递增的黄金矩形
2)根据各种比率可以分割为各种黄金动态矩形:所有矩形根据长、短边长度比值可分为两类:边长比值为有理数的矩形,如1∶2,1∶3,2∶3,3∶4,4∶5等的固定矩形。另一种是边长比值关系中存在无理数的,如1∶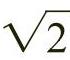 ,
, ,
,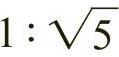 ,
,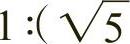
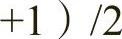 的动态矩形。
的动态矩形。
有理数比值的固定矩形分割时的平面比率是固定的,很难使人产生令人愉悦的视觉感受。这些分割往往是可预测的、有规律的而且缺乏变化的。而含无理数比值的矩形其内部分割方式和平面比率则具有很大的偶然性和不确定性,正是这种不确定性能给人带来不同的视觉感受。
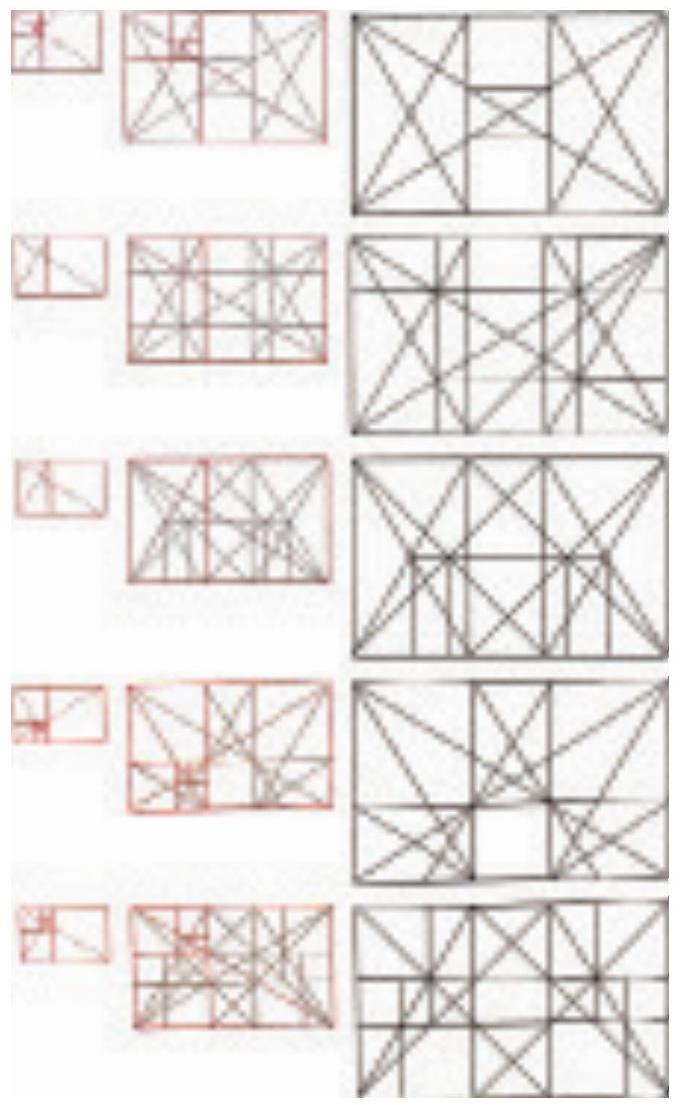
图2-31 多种黄金分割动态矩形
如图2-31所示的来自《艺术与生活中的几何学》(The Geometry of Art and life)一书中描述的一些黄金分割动态矩形图,图中五个黄金矩形均采用对角线法对其内部进行分割,分割差异虽大,但黄金矩形内部却只出现正方形和黄金矩形两种基本单元,而这两种形式都是使人愉悦的几何图形。
3.斐波纳契数列
如图2-30所示的黄金矩形的排列中,矩形的长边间具有如下特征:H3=H2+H6,H4=H3+H7,H5=H4+H8,且H1=H6,H2=H7,H3=H8,则H3=H2+H1,H4=H3+H2,H5=H4+H3。这组数列后一项的数值等于前两项的数值之和,用公式表示为:Fn=F(n-l)+F(n-2),这就是斐波纳契数(Fibonacci Number)的逻辑公式。由此可见黄金分割的特殊比例特性与斐波纳契数列的关系。
斐波纳契数列因数学家列昂纳多·斐波纳契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。早在古希腊时期就为人所熟知,特别是其与黄金分割的密切关系,因此还被称为“黄金分割数列”。在数学上,斐波纳契数列Fn是以递归的方法定义的,即
F0=0,
Fl=1,(https://www.chuimin.cn)
Fn=F(n-l)+F(n-2),
……

图2-32 斐波纳契数列
这组数列以0和1为原始值,数序为0、1、1、2、3、5、8、13、21、34……,前面两个数相加得到第三个数字,以此类推,例如,0+1=1,1+1=2,1+2=3,2+3=5等。如图2-32所示,该数列中相邻两个数字的比值非常接近黄金比率:从2开始,前一位除后一位的值近似于0.618,后一位除以前一位的数值则近似于1.618。尤其是数字377与前后数字233和610的比值最接近黄金比率。
连分数的方式能更加有效地反映数列的结构体系与倍数关系,如图2-33所示,按照连分数的方式重新排列斐波纳契数列,可以发现其形成了与黄金比率相似的“层次化”结构关系。

图2-33 斐波纳契数列与黄金比率倍数关系对比
a)斐波纳契数列的倍数关系 b)黄金比率倍数关系
4.埃及三角形
《建筑学讲义》的作者维奥莱·勒·迪克对于建筑与等腰三角形、等边三角形的关系有很深入的研究,他尤其对“埃及三角形”有特殊的兴趣。“埃及三角形”是以底边四个单位、高五个单位的直角三角形,沿长直角边镜像后拼合而成的等腰三角形。
另一种绘制埃及三角形的方法是先构建一个长八个单位、宽五个单位的矩形,连接长边两个顶点与对向长边中点形成等腰三角形(图2-34a)。维奥莱·勒·迪克在巴黎圣母院、亚眠天主大教堂与罗马康斯坦丁基督教堂中均发现埃及三角形的比例关系:底边与高的比例为8∶5,边长为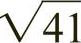 或稍大于6.4个单位。
或稍大于6.4个单位。
如图2-34b所示的等腰三角形也是由两个直角三角形组成,每个三角形的直角底边为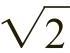 个单位,高为
个单位,高为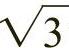 个单位,斜边是
个单位,斜边是 个单位,此时,整个等腰三角形的底边为
个单位,此时,整个等腰三角形的底边为 个单位。该等腰三角形的三条边都是无理数,因此无法通过测量得出,但是这样的比例关系的确符合建筑的中轴对称的稳定性关系,例如帕提农神庙立面,具体见第四章关于比例的相关内容。
个单位。该等腰三角形的三条边都是无理数,因此无法通过测量得出,但是这样的比例关系的确符合建筑的中轴对称的稳定性关系,例如帕提农神庙立面,具体见第四章关于比例的相关内容。
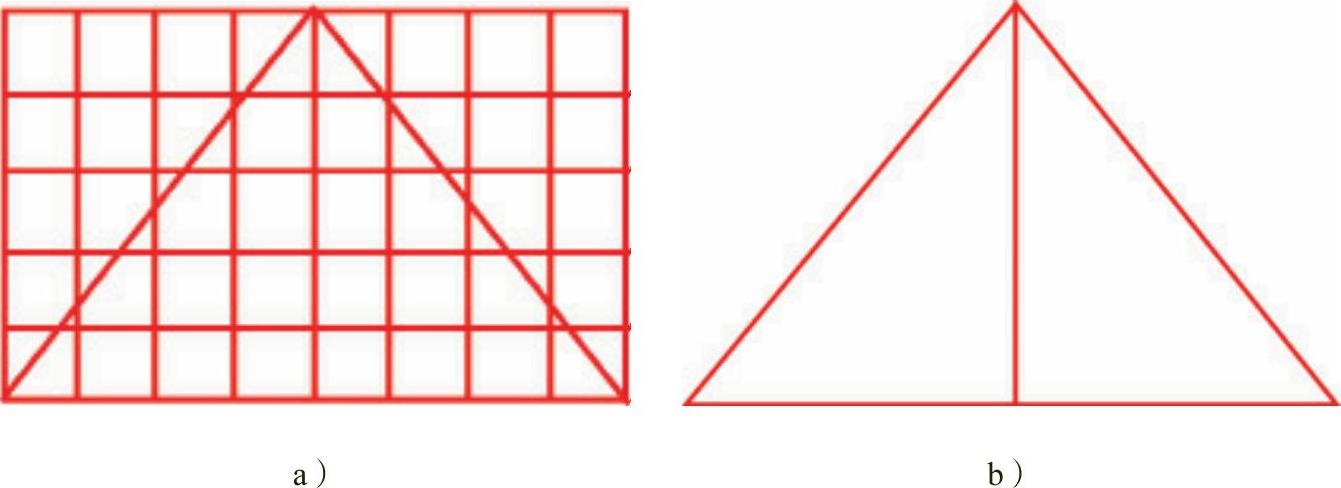
图2-34 维奥莱·勒·迪克的构图方法
5.根号矩形
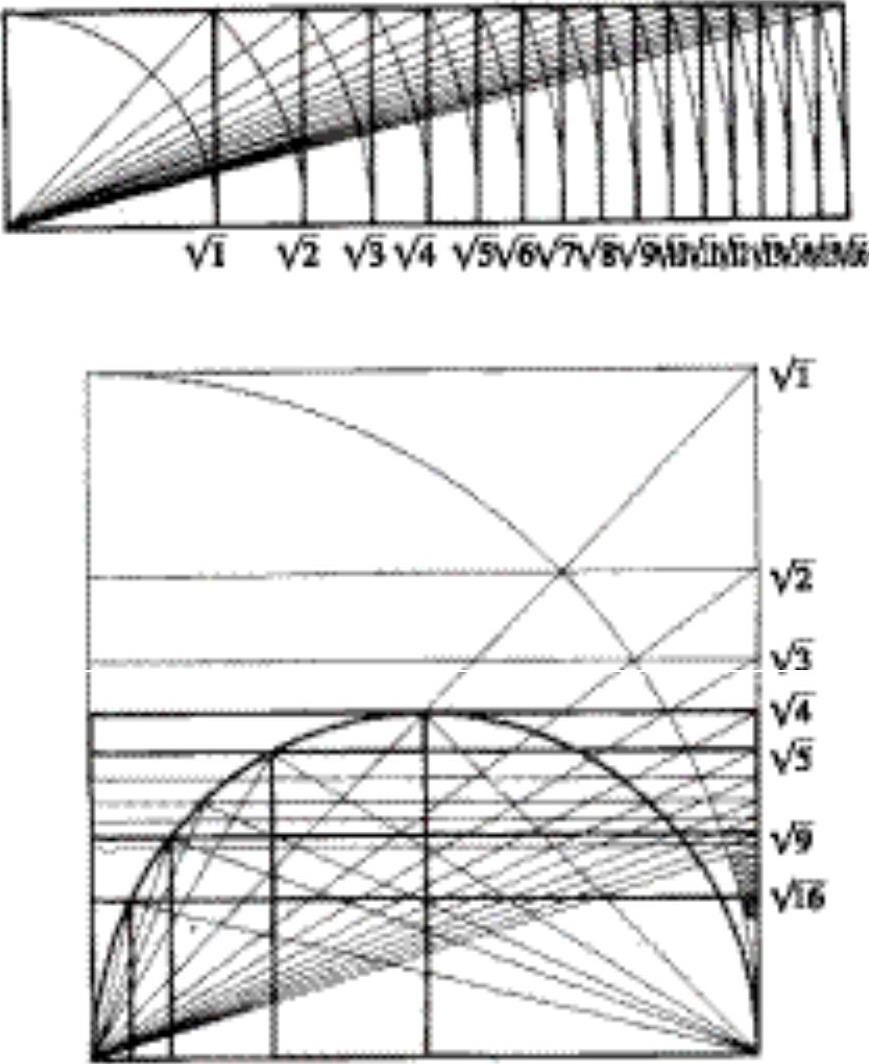
图2-35 各种根号矩形的作图方法
关于根号矩形最早的论述出现于汉布里奇的《动态对称性元素》,是以黄金分割与等差数列为基础的一种矩形关系。根号矩形的作图方法如下(图2-35):
1)先画一个正方形,以该正方形作为基础图形,正方形的边长为一个单位,此时的正方形就是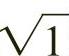 矩形。
矩形。
2)以该矩形的一个顶点为圆心,以连接该顶点的对角线长为半径做弧,该弧与正方形邻边的延长线相交,即生成新的边长为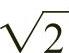 ,而由该边与原正方形边长形成的矩形是
,而由该边与原正方形边长形成的矩形是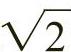 矩形。
矩形。
3)再以该顶点为圆心,以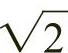 矩形对角线为半径做弧,该弧线与邻边延长线的交点形成的边长为
矩形对角线为半径做弧,该弧线与邻边延长线的交点形成的边长为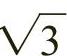 ,而该边与原正方形边长形成的矩形就是
,而该边与原正方形边长形成的矩形就是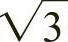 矩形。
矩形。
4)依次类推继续做出 、
、 、
、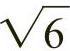 、
、 ……矩形。
……矩形。
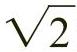 矩形的比率与黄金分割率的比例十分接近
矩形的比率与黄金分割率的比例十分接近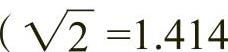 ,黄金分割率为1.618),且√2矩形具有能无限被分割成等比矩形的性质,因此该矩形成为欧洲DIN(德国工业标准)纸张尺寸体系的基础,海报、图样均使用该比例。而
,黄金分割率为1.618),且√2矩形具有能无限被分割成等比矩形的性质,因此该矩形成为欧洲DIN(德国工业标准)纸张尺寸体系的基础,海报、图样均使用该比例。而 矩形与黄金比例的关系更加紧密,如图2-36所示的以正方形底边中点为圆心,以底边中点与顶点连线为半径做圆的方式可以构成
矩形与黄金比例的关系更加紧密,如图2-36所示的以正方形底边中点为圆心,以底边中点与顶点连线为半径做圆的方式可以构成 矩形,此时
矩形,此时 矩形中正方形两侧的两个对称矩形都是黄金分割矩形。
矩形中正方形两侧的两个对称矩形都是黄金分割矩形。
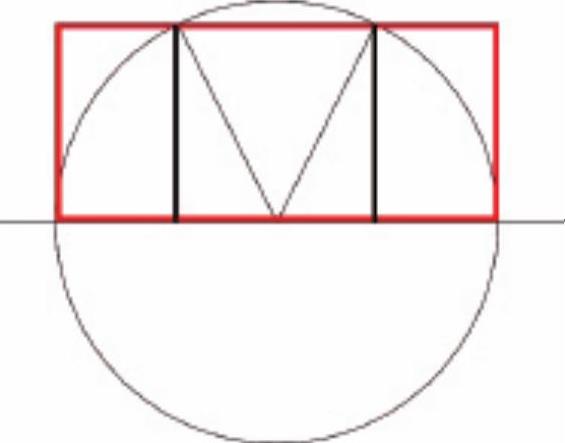
图2-36 正方形构成 矩形的方法
矩形的方法
各种根号矩形因其与黄金比例之间的联系被认为是美的,因此在平面设计、建筑立面设计中被得到广泛运用,在第四章对比例的介绍中会做具体的案例分析。
6.数列与中项
等差数列与等比数列是最常用的两种数列,在建筑设计中也时常被使用,建筑构图手法中的韵律、均衡、比例和尺度都能运用到数列的相关理论。
数列的定义:数列是指连续量值形成的体系,这个量值体系中的各量值之间存在着特定的关联或规律。
1)等差数列与等差中项:是指数列中的相邻数列之间运用加法或减法法则,通过加减运算使相邻量值间产生恒定“差值”的一组无限递增或无限递减的数列。公差是更为好理解的数列形式,设等差数列的公差为d,初始值a0,则公差中的任一项an=a0+(n-1)d。
例如,当d=2,a0=1时,a0=a1数列情况如下:
1,3,5,7,9,11,13,15,17,…
等差数列中的公差d如果是负数时,例如,当d=-2,a0=1时,数列情况如下:
1,-1,-3,-5,-7,-9,-11,-13,-15,…
也可将等差数列分解为有层次的递进关系式:
a0,
a0+d,
(a0+d)+d,
[(a0+d)+d]+d,
{[(a0+d)+d]+d}+d,
…
等差数列中决定各项数值差异的要素是公差d和初始值a0。等差数列是建筑构图中最常用的数列形式,如图2-37所示的上海金茂大厦,其建筑主体高塔部分每层平面均为正方形,但自下而上逐渐收窄,立面形成有韵律的抛物线,其自下而上的收窄分组就是按照等差数列关系逐级递减的,其中下部的13层是一组相同平面,第二组12层是一组相同平面,再向上11层平面相同,以此类推。
等差中项:等差数列中连续三项数中的中间项就是前一项与后一项的等差中项。例如上述的递进式中a0+d是a0与(a0+d)+d的等差中项,等差数列1,3,5,7,9,11,13,15,17,…中,3是1和5的等差中项,5是3和7的等差中项,以此类推。

图2-37 上海金茂大厦
2)等比数列:是指数列中的后一个量值与其前面量值是倍数的关系。等比数列可记为{an},即a1,a2,a3,…,a1是数列的“首项”,a2是数列的“第二项”,依此类推。等比数列的通项式为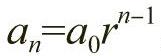 ,其中r为公比,a0作为已知初始值,a1=a0。等比数列中前n项的和符合公式:
,其中r为公比,a0作为已知初始值,a1=a0。等比数列中前n项的和符合公式: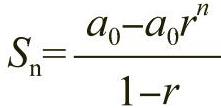 。
。
例如,当r=2,a0=1时,数列情况如下:
1,2,4,8,16,32,64,128,256,…
当r=3,a0=2时,数列情况如下:
2,6,18,54,162,486,1458,…
如果将等比数列以简洁“幂”的方式表达,可以写作:
aOr0,aOr1,aOr2,aOr3,aOr4,a0r5,…
例如,当r=2,a0=1时,数列情况如下:
20,21,22,23,24,25,26,…
由上述示例可知等比数列中的初始值a0和公差r是决定数列形式和属性的决定要素。公差r作为一个固定的倍数,根据初始值和数列前项的数值决定数列中后项的数值,而前项与后项的数值差由公差r的大小决定。
建筑构图学中的构图手法韵律与比例中广泛运用等比数列理论。通过控制等比数列中初始值a0和公差r的参数,可以得到不同的建筑比例与建筑造型。
等比中项:等比数列中连续三项数中的中间项就是前一项与后一项的等比中项。例如上面的递进式中22就是21与23的等比中项。
相关文章

例如古希腊建筑构图元素中的柱式重复排列和黄金分割比例,中国古代建筑中的对称等。以上三原则即是形态构成原则也是建筑构图原则。建筑构图的三个基本原则来自于“均衡、稳定、统一和变化”等美学原理。好的建筑构图成果要达到这三原则的标准,建筑师除了解建筑掌握建筑构图手法外,还需要了解形态相关概念、视觉要素属性、几何学要素属性与关系及完形心理学相关理论。......
2025-09-30

迪朗将建筑分为水平部分(平面)、垂直部分(立面),迪朗认为建筑设计的出发点并非“空间”,而是构成空间的平面和立面,以及由面围合而成的“体”。而成立于1866年的莫斯科绘画雕塑和建筑技术学院则沿袭布扎体系的教学方式,将“构图”的相关知识贯穿于建筑设计、绘画与雕塑的课程教授中。......
2025-09-30

形状是识别形体、给形体分类的主要依据。线形与面形通常是建筑平立面构图中的主要要素,而体形是建筑立体构图中空间内构成的主要要素。3)体量与组成其形体的元素的密度相关,一定体积的形体内组成元素的填充密度越大或元素的自身密度越大,形体的体量越大。......
2025-09-30

图3-14双层玻璃幕墙结构图2.建筑的美学设计要求BIPV建筑首先是一个建筑,它是建筑师的艺术品,就相当于音乐家的音乐,画家的一幅名画,而对于建筑物来说光线就是它的灵魂,因此建筑物对光影要求甚高。......
2025-09-29

(一)建筑本身即为景观建筑不但要为人类提供舒适的居住条件,同时,作为空间环境的主要实体与空间形态的构成要素,其本身就是一种景观元素。景观建筑是现代景观理念、方法和文化背景相结合而形成的对建筑设计的新的审美方式和创作手段。......
2025-09-30

单层建筑中或多层建筑的两自然结构楼层间局部有楼层者,按其水平投影面积计算建筑面积。2)单层碉台及多层碉台的首层,有台明的按台明外围水平面积计算建筑面积,无台明的按围护结构底面外围水平面积计算建筑面积。两层或多层建筑构架柱外有围护装修或围栏的挑台部分,按构架柱外边线至挑台外围线间的水平投影面积的二分之一计算建筑面积。......
2025-09-30

图6-36斜透视图6-36斜透视图6-37画面前后位置不同时的透视6.5.2.2画面同建筑物的前后关系画面的方向虽已确定,但尚可前后移动。......
2025-09-29

图2-5是一个典型的脊骨结构实例——美国费城53层的Bell Atlantic Tower[29]。图2-5 脊骨结构实例——Bell Atlantic Towera)建筑平面轮廓 b)周边框筒或框架方案 c)脊骨结构方案图2-5 脊骨结构实例——Bell Atlantic Tower(续)d)脊骨结构图2-6 脊骨结构的剪力膜a)多层对角支撑 b)外伸空腹桁架 c)单跨空腹桁架 d)滑动铰......
2025-09-30
相关推荐