伸臂设置位置和数量要诀

2023-08-23 理论教育版权反馈

【摘要】：有关伸臂结构合理位置的研究很多，一般都以减小侧移为目标函数来研究伸臂的最优位置。图9-2 伸臂设置效果影响因素a）γ—Ry关系 b）α—Ry关系 c）一道伸臂的优化位置 d）两道伸臂的优化位置 e）多道伸臂的效果图9-2b表示改变参数α对Ry的影响，其他参数不变。3）设置多道伸臂时，会进一步减小位移，但位移减小并不与伸臂数量成正比，设置伸臂多于4道时，减小侧移的效果基本稳定。

在高层建筑中都需要有避难层和设备层，通常都将伸臂和避难层、设备层设置在同一层，因此，结构工程师布置伸臂时要考虑建筑布置和设备层布置的要求，同时，也要从结构合理的角度与建筑师进行协商。作为结构工程师，必须了解伸臂位置对结构受力的影响，并知道其合理的位置，才能从结构的角度提出建议，制订出各方面都合理的综合优化布置方案。

有关伸臂结构合理位置的研究很多，一般都以减小侧移为目标函数来研究伸臂的最优位置。研究大多是建立在某种计算简图的基础上，设定某些条件，采用函数关系求极值的方法。研究时采用的计算简图一般都是平面模型，早期研究采用的计算模型见图9-1a，只考虑伸臂与外柱铰接，假定外柱只有轴向变形，且不考虑楼板大梁的作用，与实际情况有些出入。

图9-1b是改进了的计算模型，其外柱可以模拟周边框架或框筒（图9-1c），因此外柱具有轴向刚度（EA）和弯曲刚度（EI），伸臂与外柱刚接，每个楼层都有刚接的楼板大梁。图9-1b模型中符号EI_F，EA_F分别代表外框架的弯曲及轴向刚度，EI_b代表伸臂的刚度，EI_c代表内筒刚度，EI_l代表楼板大梁刚度，每层楼板大梁截面不变。

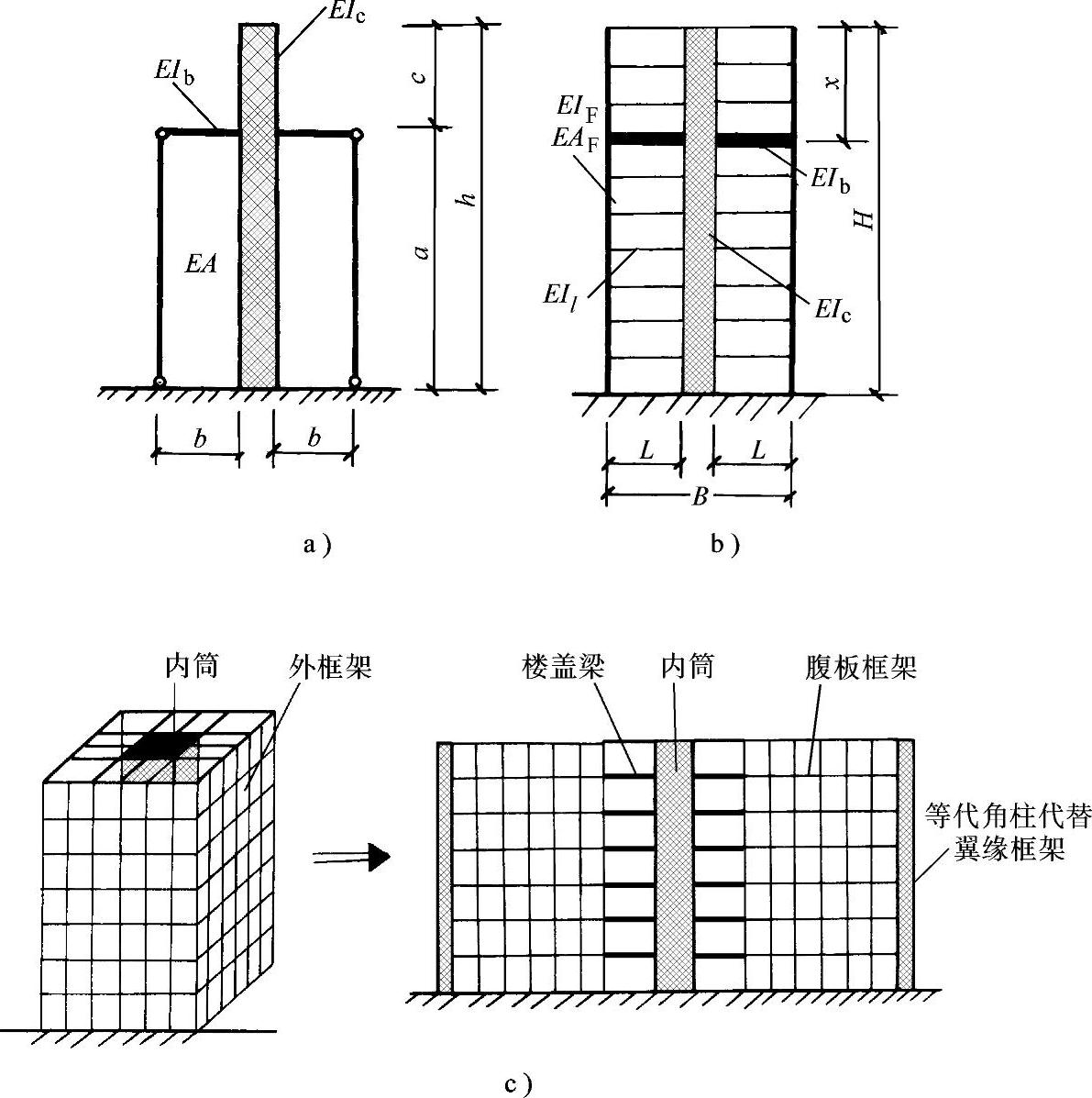
图9-1 伸臂设置优化计算模型（清华大学）

图9-2是用图9-1b模型进行优化分析后整理得到的几个变量和减小侧移效果的关系曲线[66]，设定的变化参数有3个：

外框架线刚度与伸臂大梁线刚度比值

伸臂大梁线刚度与内筒线刚度的比值

伸臂大梁设置位置的相对坐标

ξ=x/H （9-1c）

图中R_y为设置伸臂结构的顶点侧移与无伸臂结构顶点侧移的比值，R_y愈小，表示减小侧移的效果愈好。

图9-2a表示改变参数γ对R_y的影响，其他参数不变。当γ增大，即外框架的刚度增大时，设置伸臂的效果减小，框筒的γ值一般在20以上，此时R_y>0.9，设置伸臂对减少侧移的影响很小，小于10%。

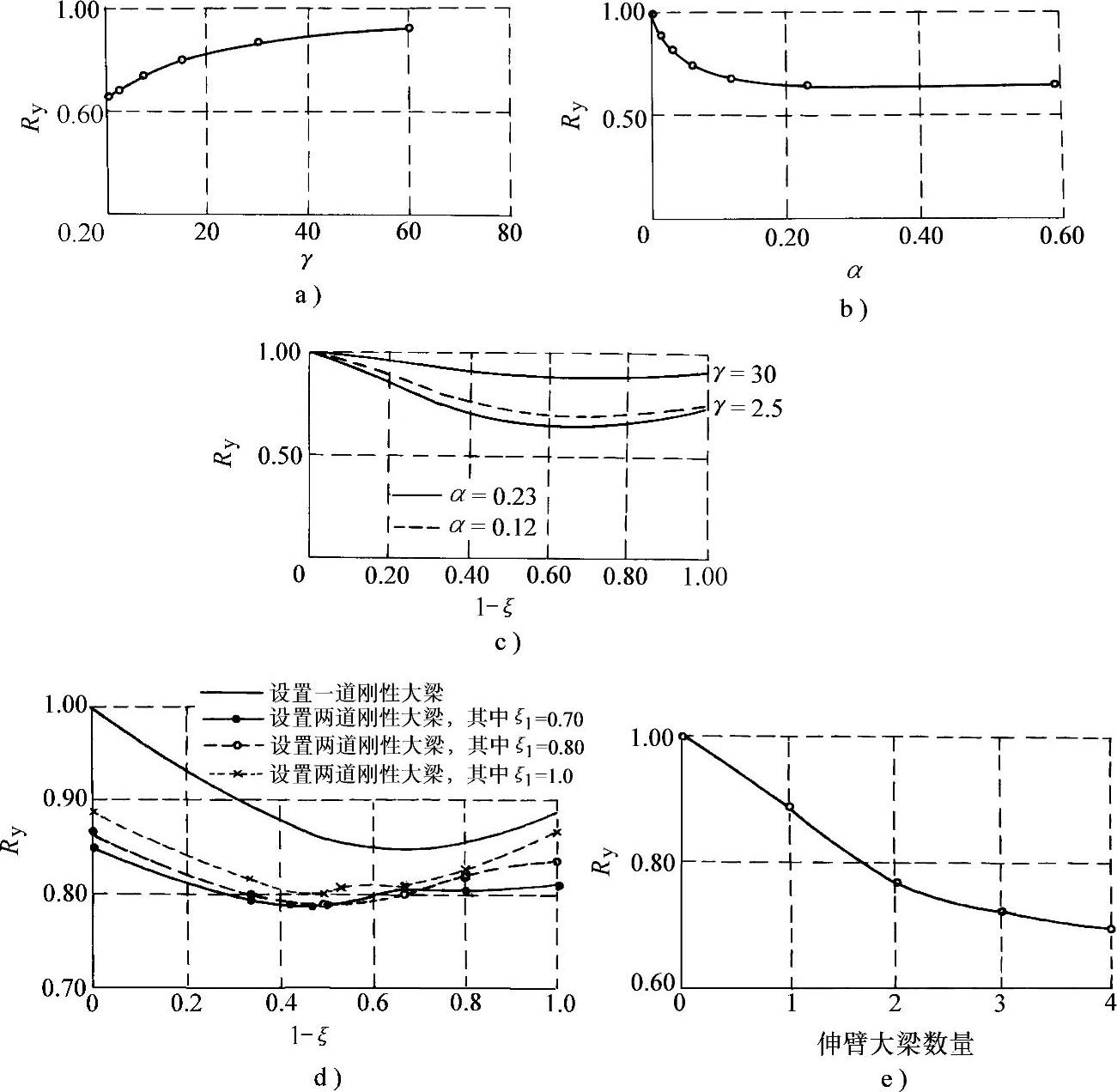
图9-2 伸臂设置效果影响因素（清华大学）

a）γ—R_y关系 b）α—R_y关系 c）一道伸臂的优化位置 d）两道伸臂的优化位置 e）多道伸臂的效果

图9-2b表示改变参数α对R_y的影响，其他参数不变。当α由0增大到0.1左右时，设置伸臂的效果明显加大，说明在α≤0.1时，增大伸臂大梁的刚度对减小侧移影响明显，α继续增大时效果变化很小，伸臂大梁的刚度太大并没有必要。

图9-2c表示设置一道伸臂时，伸臂的最优位置约在（0.6～0.7）H之间，具有不同α参数所得结果相差不大，而γ值增大时（采用框筒，γ=30），伸臂效果大大减小，最优位置不明显。

图9-2d表示设置两道伸臂时伸臂的最优位置，与设置一道伸臂相比，设置两道伸臂减小侧移的效果较大。图中比较了三种情况，每种情况中的较高一道伸臂的位置已经设定，三种情况的结果相差不大，若其中一道设置在接近顶部的楼层，则另一道设在0.5H左右效果较好。

图9-2e给出了设置多道伸臂效果的比较，伸臂数量增加，减小侧移效果也增加，但是其效果并不与数量成正比，伸臂增多后侧移减小的效果增长减缓。

类似的研究很多，计算简图有差异，考虑的影响因素也有所不同，但是所得结果大同小异，说明最优位置对各种因素并不十分敏感，从结构设计角度，着重于概念和大体的优化位置，因此可综合如下：

1）当只设置一道伸臂时，最佳位置在底部固定端以上（0.60～0.67）H之间，H为结构总高度，也就是说设置一道伸臂时，大约在结构的2/3高度处设置伸臂效果最好。

2）设置两道伸臂的效果会优于一道伸臂，侧移会更减小；当设置两道伸臂时，如果其中一道设置在0.7H以上（也可在顶层），则另一道设置在0.5H处，可以得到较好的效果。

3）设置多道伸臂时，会进一步减小位移，但位移减小并不与伸臂数量成正比，设置伸臂多于4道时，减小侧移的效果基本稳定。当设置多道伸臂时，一般可沿高度均匀布置。

4）当外框架的刚度不大时，设置伸臂对减小侧移有较明显的效果；当结构周边采用抗侧刚度很大的框筒时，设置伸臂对减小侧移的效果不大。

从有关参数及优化位置得到的一些概念，设计时必须综合考虑建筑使用、结构合理、经济美观等各方面要求，得到综合比较后的最优方案。

伸臂设置位置和数量要诀

相关推荐