计算结果从另一方面清楚地说明了延性连梁和脆性连梁对双肢剪力墙的影响。图7-23给出了地震反应分析结果，比较了最大侧向位移包线、连梁延性系数包线、最大倾覆力矩包线和最大轴向力包线。在实际结构中，美洲银行的连梁虽然出现了剪切斜裂缝，但还没有完全丧失强度和刚度，因此地震时墙肢并没有屈服。由美洲银行的分析可见，联肢剪力墙中对连梁的延性要求很高，普通配筋设计的连梁很难达到。......
2023-08-23
高层建筑钢筋混凝土结构：连梁对联肢剪力墙弹塑性性能分析
【摘要】：上节中提到的美国伯克利加州大学所作的双肢剪力墙试验以及对它所作的系列分析可以进一步说明连梁对开洞剪力墙弹塑性阶段的受力和破坏性能的影响。对15层双肢剪力墙所作的弹塑性系列分析主要是改变连梁的尺寸和配筋，共分析了七种情况，其墙肢尺寸和配筋与原试验模型完全相同。
上节中提到的美国伯克利加州大学所作的双肢剪力墙试验以及对它所作的系列分析可以进一步说明连梁对开洞剪力墙弹塑性阶段的受力和破坏性能的影响。
美国伯克利加州大学所作的双肢剪力墙试验模型（图7-19c），是模拟一个按照美国规范进行设计的15层双肢剪力墙，见图7-20a，取出底部4层做成模型进行加载试验，顶部施加的弯矩、轴力及剪力模拟了15层结构中传至底部4层的荷载，见图7-20b。试验结果发现实测的刚度和承载力都大大超过设计时预期的刚度和破坏荷载，见图7-20c，而且出现了受压墙肢的剪压破坏。试验时量测了墙肢轴向力，一个墙肢出现拉力（水平荷载下的弯曲拉力超过竖向荷载下的轴力），另一个墙肢则轴向压力很大，大大超过了设计值，由于墙肢轴向力增大而使受弯承载力大大增加。问题是为什么墙肢轴向力超过了设计值？
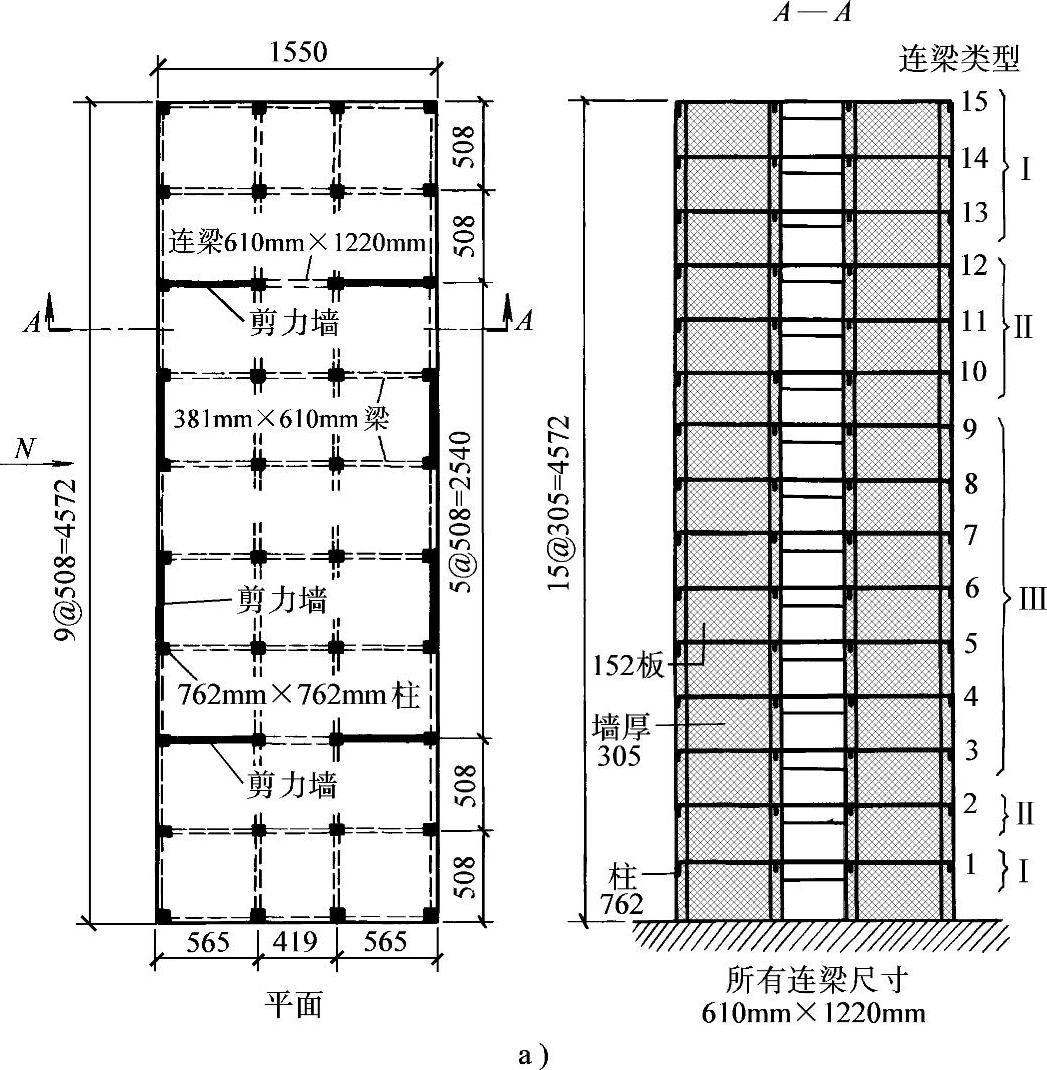
图7-20 美国伯克利加州大学所作的双肢剪力墙试验
a）原结构平面及15层双肢剪力墙立面
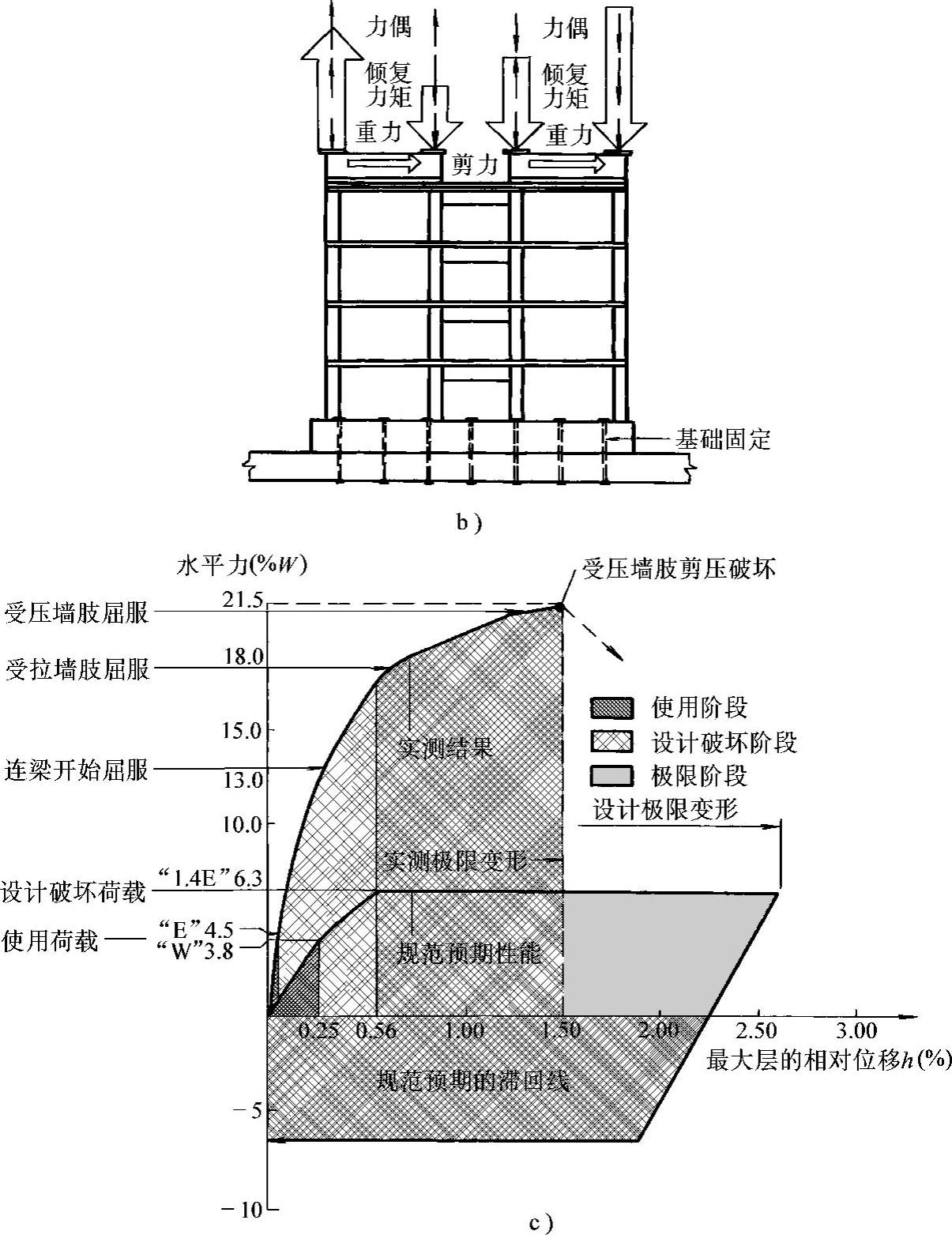
图7-20 美国伯克利加州大学所作的双肢剪力墙试验（续）
b）底部4层试验模型及顶部荷载 c）试验与设计预期的位移和承载力
本书作者在V.V.Bertero教授指导下对该15层剪力墙进行了改变连梁参数的系列弹塑性静力分析（推覆分析）[62]，说明了连梁对联肢剪力墙弹塑性性能的影响（分析时假定连梁符合强剪弱弯条件，不会出现剪切破坏）。
对15层双肢剪力墙所作的弹塑性系列分析主要是改变连梁的尺寸和配筋，共分析了七种情况，其墙肢尺寸和配筋与原试验模型完全相同。图7-21比较了该计算系列剪力墙的基底剪力—顶点位移曲线。图中CW—1p墙的连梁与试验模型相同，相对于其他六片墙，它的连梁尺寸及配筋都是最大的，弹塑性分析得到的承载力、顶点位移与试验结果基本吻合，这片墙的承载能力最大，刚度也最大，而且受拉墙肢出现了水平贯通裂缝；CW—1A、1B、1C、1D四片墙减小了连梁尺寸及配筋，这四片墙连梁的尺寸并不相同，但通过不同的配筋使四片墙连梁的刚度和屈服弯矩接近。由图7-21可见，计算得到的这四片墙的刚度和承载力相差不大，都低于CW—1P墙的刚度和承载力，受拉墙肢中仅有很小拉力或没有拉力；CW—1E墙的连梁尺寸和配筋都减小，所得剪力墙的刚度和承载力也都减小，直到破坏时受拉墙肢还有相当大的压力；最后一片墙CW—1G的连梁刚度和抗弯承载力都为0，即相当于两个独立剪力墙并联抵抗水平荷载，由图7-21可见，它的刚度和承载力都是最小的。
图7-21 弹塑性分析的基底剪力—顶点位移曲线比较（清华大学）
上述分析表明，当墙肢相同、且连梁不被剪坏的条件下，连梁的弹性刚度对双肢剪力墙的初始刚度影响较大，而连梁的配筋和抗弯承载力对双肢剪力墙的最大承载力影响很大，对墙肢中的轴力影响很大。这是因为：①连梁弯矩就是连梁对墙肢的约束弯矩，约束弯矩大可加大双肢剪力墙的抗倾覆力矩Nl；②连梁的弯矩大，剪力就大，连梁剪力直接影响墙肢的轴力，当连梁截面及配筋加大时，受拉墙肢拉力增大，甚至超过重力作用下的轴向压力而使墙肢受拉，从而出现贯通水平裂缝，受压墙肢则因为轴向压力加大而提高了墙肢的抗弯承载力M2u。由平衡关系Mpu=Mlu+M2u+Nll可知，最终使剪力墙的承载力提高。
连梁尺寸过小，不利于增大剪力墙刚度，如果连梁配筋过小，连梁会在使用荷载下出现裂缝，甚至屈服，不利于正常使用；反之，尺寸较大或配筋过大的连梁也是不利的，虽然它提高了剪力墙的承载力，但是使剪力墙延性降低，甚至使受压墙肢出现剪压破坏。
为什么受压墙肢会出现剪压破坏？由墙肢中的剪力重分配可以进一步了解受压墙肢的剪力在弹塑性阶段也是逐步加大的，由上述计算得到两个墙肢的剪力重分配过程示于图7-22，该图的横坐标是VB/Vmax（表示剪力墙总剪力达到最大抗剪承载力的百分数），纵坐标是VC/VB（表示受压墙肢的剪力达到剪力墙总剪力的百分数）。在弹性阶段，受压墙肢与受拉墙肢的剪力相等（因为两个墙肢截面相等，刚度相等），VC/VB=0.5，受拉墙肢屈服以后刚度降低，就出现了内力重分配，受压墙肢的剪力直线增加，直到它自己的竖向钢筋也屈服为止，受压墙肢剪力下降一个过程以后逐步稳定，然后受压墙肢的剪力又重新上升，直到破坏。受拉墙肢开裂使刚度降低，受压墙肢轴力加大会使它刚度增大，二者刚度相差，导致剪力向刚度较大的受压墙肢转移，最后A、B、C、D四片剪力墙的受压墙肢剪力达到总剪力的70%左右，而CW—1P墙的连梁最强，其受压墙肢剪力达到了总剪力的80%以上。计算结果印证了伯克利加州大学所作试验的实测结果，试验模型在破坏前实测到的受压墙肢剪力约为总剪力的90%，与计算结果接近。模型按照弹性计算的剪力设计抗剪配筋（受压墙肢承受的剪力只有50%），实际剪力大大超过了它的抗剪承载力，所以受压墙肢出现了剪压破坏。
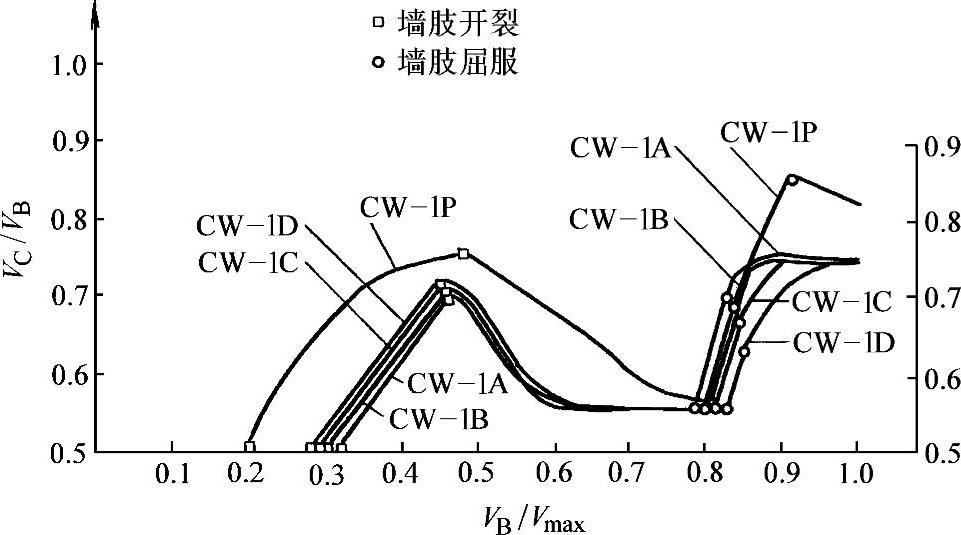
图7-22 双肢剪力墙墙肢剪力重分配过程（清华大学）
由以上分析可知，在抗震设计时，要充分估计联肢剪力墙中受压墙肢所受的剪力（在反复荷载作用下，每一侧的墙肢都可能是受压墙肢），不能只用弹性计算的剪力来设计墙肢受剪承载力，应当调整受压墙肢的剪力，从而防止墙肢在弹塑性状态下的受剪破坏。
有关高层建筑钢筋混凝土结构概念设计的文章
- 详细阅读
-
高层建筑钢筋混凝土结构概念设计：弹塑性时程分详细阅读
无论是基于承载力延性的抗震设计，还是基于性能的抗震设计，都需要用到弹塑性时程分析或弹塑性静力计算，目前计算软件已有较大改进，应用日益广泛。通常，弹性时程分析采用杆模型，弹塑性时程分析采用层模型；用于研究时采用杆模型，用于设计第二阶段的倒塌验算时，采用层模型等。......
2023-08-23
-
高层建筑连梁设计措施详细阅读
5）跨高比小于2.5的连梁多数出现剪坏，为避免脆性剪切破坏，主要措施是控制剪压比和适当增加箍筋数量。7）当连梁破坏对承受竖向荷载没有很大影响时，在大震作用下，允许连梁剪切破坏，按照多道设防的概念设计联肢剪力墙。......
2023-08-23
-
高层建筑连梁弯矩调幅概念设计详细阅读
由表可见，在7度设防区，剪力墙结构中连梁的刚度折减系数不宜小于0.5，否则连梁弯矩折减系数将小于0.8，在8度、9度设防区，如果需要，连梁刚度还可折减多一些。图7-36 kl，max—α关系曲线表7-6 连梁刚度折减0.5时，kl，max的折减系数必须注意，上述内力折减系数是取连梁刚度折减所得到的结果。......
2023-08-23
-
高层建筑钢筋混凝土结构概念设计：剪力墙中的强详细阅读
应该设计“强墙弱梁”的联肢剪力墙。但是由于连梁对剪切变形敏感，容易剪坏，也可能在出现塑性铰后不久就剪坏，从而会形成d类情况，只要按照多道设防原则设计墙肢，这种情况仍然是可以继续抵抗地震的。......
2023-08-23
-
2.15.7剪力墙与连梁：全国注册结构工程师详细阅读
对于普通箍筋连梁，一级抗震等级取1.3，二级取1.2，三级取1.1，四级取1.0；配置有斜向钢筋的连梁ηvb取1.0。2）斜截面受剪承载力应符合下式要求：11.连梁配筋构造剪力墙及筒体洞口连梁的纵向钢筋、斜筋及箍筋的构造应符合下列要求：连梁沿上、下边缘单侧纵向钢筋的最小配筋率不应小于0.15%，且配筋不宜少于2φ12；交叉斜筋配筋连梁单向对角斜筋不宜少于2φ12，单组折线筋的截面面积可取为单向对角斜筋截面面积的一半......
2023-08-28
-
高层建筑钢筋混凝土结构概念设计：剪力墙的破坏详细阅读
图7-1 悬臂墙的破坏形态a）弯曲破坏 b）弯剪破坏 c）剪切破坏 d）滑移破坏1.剪跨比剪跨比表示截面上弯矩与剪力的相对大小，是影响剪力墙破坏形态的重要因素。......
2023-08-23
-
联肢剪力墙的裂缝分布和破坏形态分析详细阅读
在水平荷载作用下，联肢剪力墙的墙肢可能出现弯曲破坏或剪切破坏，墙肢的内力分布和破坏形态与连梁刚度和连梁承载力有密切关系。另一种情况是联肢剪力墙中受压墙肢的剪坏，美国伯克利加州大学所作的双肢剪力墙就出现了这种破坏，原因是在塑性变形的过程种受压墙肢的剪力增大，设计时对其估计不足而使墙肢受剪承载力不够，造成墙肢剪压破坏[61]。......
2023-08-23
相关推荐