在水平荷载作用下,联肢剪力墙的墙肢可能出现弯曲破坏或剪切破坏,墙肢的内力分布和破坏形态与连梁刚度和连梁承载力有密切关系。另一种情况是联肢剪力墙中受压墙肢的剪坏,美国伯克利加州大学所作的双肢剪力墙就出现了这种破坏,原因是在塑性变形的过程种受压墙肢的剪力增大,设计时对其估计不足而使墙肢受剪承载力不够,造成墙肢剪压破坏[61]。......
2023-08-23
为了对联肢剪力墙的性能有深入的理解,首先介绍由连续化方法得到的联肢剪力墙的一些弹性内力计算公式,通过计算分析了解联肢剪力墙的主要规律。
图7-11a表示一个联肢剪力墙切开截面的内力,由连续化方法得到的墙肢内力可以表达成下列公式[6]:
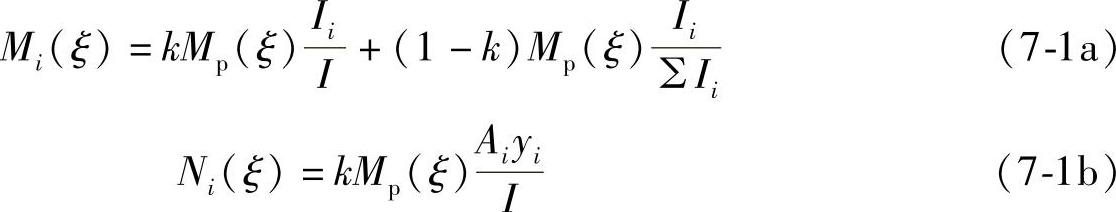
式中 Mp(ξ)——坐标ξ处外荷载作用的倾覆力矩,ξ=x/H,为截面的相对坐标;
Mi(ξ)、Ni(ξ)——坐标ξ处第i墙肢的弯矩和轴力;
Ii、yi——第i墙肢的截面惯性矩、截面重心到剪力墙总截面重心的距离;
I——剪力墙截面总惯性矩,I=ΣIi+ΣAiy2i
k——系数。
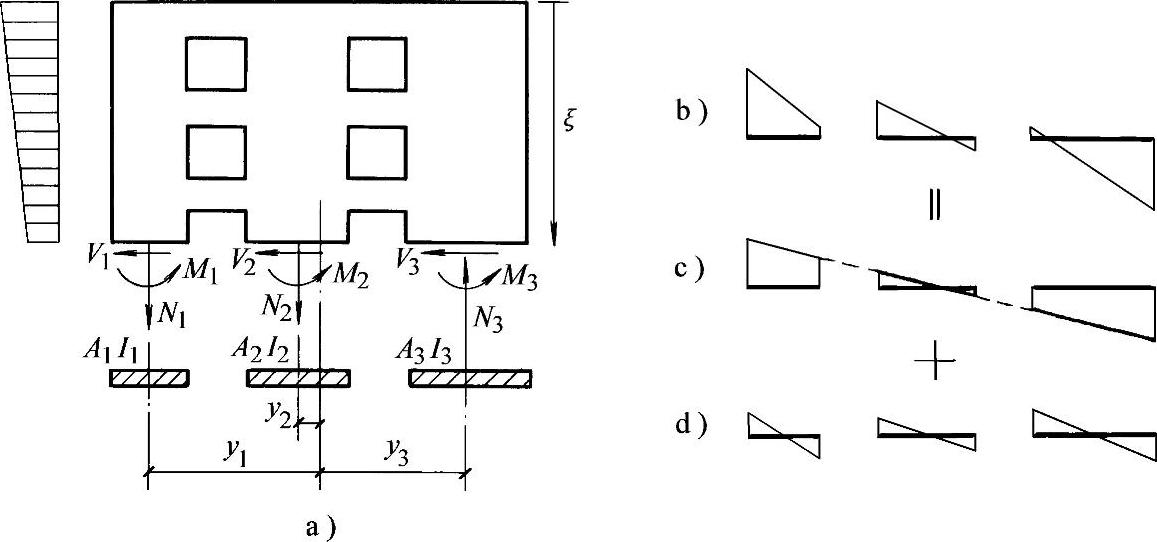
图7-11 联肢墙截面应力的分解
式(7-1)的物理意义可由图7-11说明。图7-11b表示联肢肢剪力墙截面应力分布,它可分解为c、d两部分:c图的应力沿全截面直线分布,称为整体弯曲应力,组成每个墙肢的部分弯矩及轴力,分别对应于式(7-1a)和(7-1b)的第一项;d图为每个墙肢的另一部分应力,称为局部弯曲应力,组成另一部分弯矩(没有轴力),对应于公式(7-1a)的第二项;两部分弯矩叠加成为墙肢弯矩。
系数k表示两部分弯矩的百分比,k值较大,则整体弯曲应力较大(图7-11c),局部弯曲应力较小(图7-11d),此时截面上总应力分布(图7-11b)更接近直线,接近整体悬臂剪力墙截面的应力分布,可能一个墙肢完全为拉应力,另一个墙肢完全为压应力,墙肢的轴向力较大而弯矩较小;k值较小则反之,截面上应力锯齿形分布更明显,每个墙肢都会有拉、压应力,墙肢的弯矩较大而轴向力较小。
系数k值与荷载形式有关,在倒三角分布荷载下,k值计算公式为[59]:
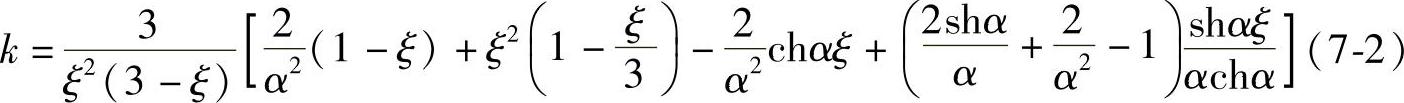
系数k是坐标ξ和整体系数α的函数。整体系数α表示连梁与墙肢相对刚度,α是由连续化方法推导内力计算公式时得到的一个系数,式(7-3a)给出了双肢剪力墙的整体系数α[6][9]:

式中 H、h——剪力墙的总高与层高;
I1、I2、Il——两个墙肢和连梁的惯性矩;
a、c——洞口净宽的一半和墙肢重心到重心距离的一半。
T——墙肢轴向变形影响系数;

α系数只与联肢剪力墙的几何尺寸有关,为已知几何参数,α愈大表示连梁相对刚度愈大,它对联肢墙内力分布和位移的影响很大,因此是一个重要的几何参数。
计算k值的式(7-2)可以画成图7-12的曲线族,截面所在位置坐标ξ不相同,k值曲线不同,由k—α—ξ关系可以分析α的影响。该族曲线的共同特点是:当α很小时,k值都很小,截面内以局部弯矩为主;当α增大时,k值增大,α大于10以后,k值都趋近于1,也就是截面应力分布接近直线,以整体弯矩为主,随着墙肢的轴力加大而弯矩减小。
如果联肢墙的α很小(α≤1),意味着连梁对墙肢的约束弯矩很小,此时可以忽略连梁对墙肢的影响,把连梁近似看成铰接连杆,墙肢成为单肢墙,见图7-13,计算时可看成多个单片悬臂剪力墙并联,这种情况下的连梁可称为“弱连梁”。
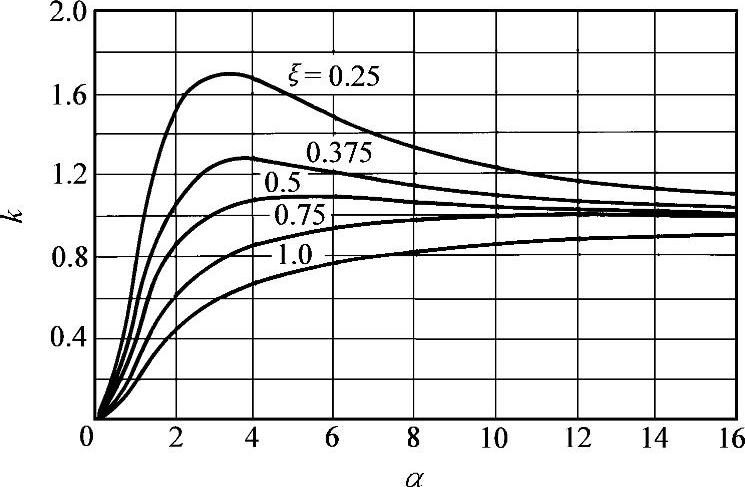
图7-12 倒三角分布荷载下k—α—ξ曲线族
图7-13 连杆连接的独立墙肢
整体系数α是联肢剪力墙的一个重要几何参数,整体系数α表示连梁与墙肢的相对刚度。α系数影响墙肢内力分布,α较小时k值小,墙肢内以局部弯曲为主,α≤1时可近似看作几个独立墙肢;α较大时k值大,α>10时,k值趋近1,墙肢内以整体弯曲为主。
整体系数α不仅与墙肢内力分布有关,它对连梁内力分布也有很大影响。由连续化方法得到的连梁剪力可以表达为下列公式:

式中,V0是剪力墙的基底剪力,kl是与荷载分布形式有关的系数,式(7-5)是倒三角分布荷载作用下的kl表达式,式中符号同前。
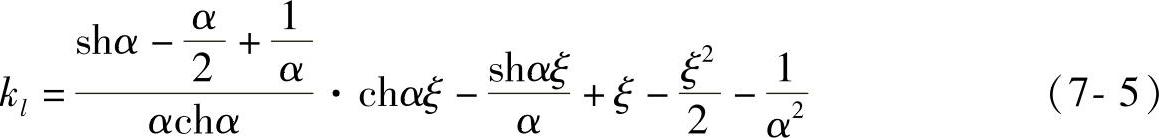
系数kl也是坐标ξ和整体系数α的函数,式(7-5)可画成图7-14的曲线族,可看到具有不同α值剪力墙的kl系数沿高度的分布形式,也就是连梁剪力沿高度的分布形式。由图7-14可见,连梁剪力的最大值不在底层,而是在剪力墙中部偏下的某个高度处,随着α的增大,连梁剪力的最大值也随之增大,但其所在位置下降。
整体系数α影响可归纳为:
1)α值增大时,连梁剪力增大;连梁最大剪力在中部偏下某个高度处,α愈大,其位置愈接近底截面。
2)墙肢轴力与α有关,因为墙肢轴力即该截面以上所有连梁剪力之和,当α值加大时,连梁剪力加大,墙肢轴力也加大。
3)墙肢的弯矩与α值有关,与轴力正好相反,α值愈大,墙肢弯矩愈小。这也可以从平衡的观点得到解释,任意一个墙截面平衡要求:
M1+M2+N·2c=Mp (7-6)
所以,在相同的外弯矩Mp作用下,N愈大,M1、M2就要减小。
4)α值增大时,连梁对墙肢的约束弯矩增大;连续化计算的内力沿高度是连续分布的,实际上由于连梁不是连续的,连梁剪力和对墙肢的约束弯矩也不是连续的,在连梁与墙肢相交处,墙肢弯矩、轴力会有突变,形成锯齿形分布,见图7-15,α值愈大,连梁约束弯矩愈大,弯矩突变(即锯齿)也愈大。
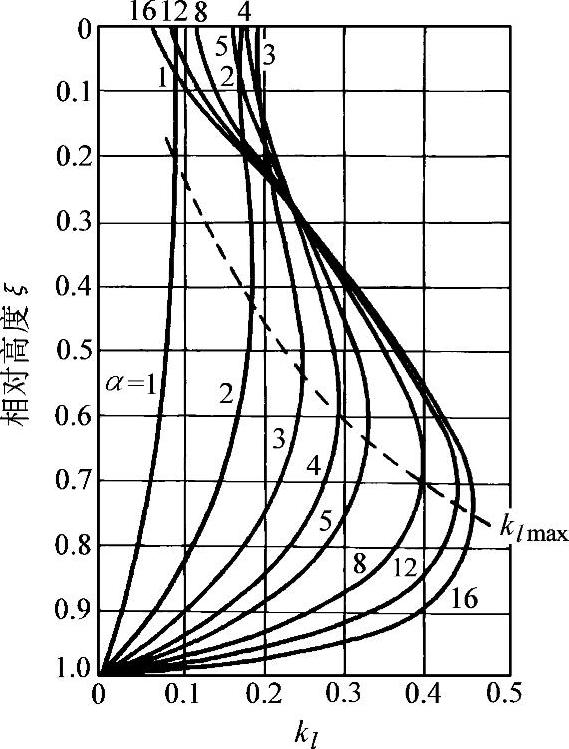
图7-14 倒三角分布荷载下 ξ—kl—α关系曲线
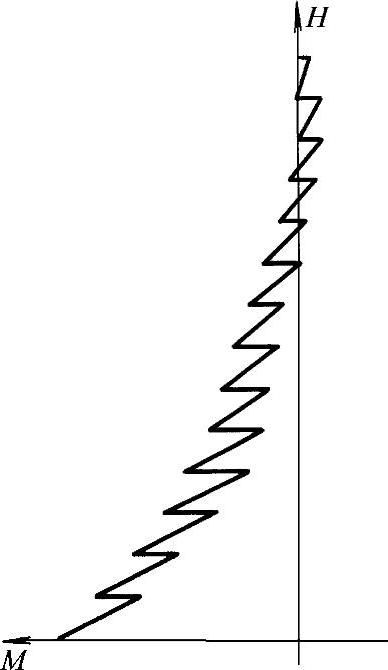
图7-15 连梁约束弯矩和墙肢弯矩分布图
整体系数α对联肢剪力墙的影响,实际就是连梁刚度对联肢剪力墙的影响,它不但影响弹性内力分布,同样也会影响到联肢剪力墙弹塑性性能,影响联肢剪力墙的裂缝分布和破坏形态,下面将会进行详细分析。
有关高层建筑钢筋混凝土结构概念设计的文章

在水平荷载作用下,联肢剪力墙的墙肢可能出现弯曲破坏或剪切破坏,墙肢的内力分布和破坏形态与连梁刚度和连梁承载力有密切关系。另一种情况是联肢剪力墙中受压墙肢的剪坏,美国伯克利加州大学所作的双肢剪力墙就出现了这种破坏,原因是在塑性变形的过程种受压墙肢的剪力增大,设计时对其估计不足而使墙肢受剪承载力不够,造成墙肢剪压破坏[61]。......
2023-08-23

中性层与横截面的交线,称为中性轴。概括地说,纯弯曲时梁的所有横截面仍保持平面,并绕中性轴做相对转动,而纵向“纤维”则均处于单向受力状态。式(7-5)表明了梁横截面上正应力的变化规律。而要确定截面上某点的正应力的大小,还需建立应力与内力之间的静力关系。纯弯曲时梁横截面任意点的正应力计算公式,在一定条件下也适用于横力弯曲。......
2023-06-19

根据已有的研究成果,框架断路器动导电杆上70%的电动斥力来自于触头区域电流收缩引起的Holm力,其余来自导电回路。根据Holm力简化计算公式可知,Holm力与电流的平方成正比,故动导电杆上Tr峰值分布与电流峰值分布规律接近。图7-13 软连接截面磁感应强度的分布......
2023-06-15

电路图一般由电路原理图、技术说明和标题栏组成。确切表明了各元器件间的组成、相互关系和工作原理。元器件明细栏均以表格的形式写在标题栏的上方。元器件明细栏(表)的组成明细栏一般由序号、代号、名称、数量、材料、质量、分区、备注等组成,也可按实际需要增加或减少。明细栏的尺寸与格式如图4-1所示。其顺序应是由上而下延伸,还可连续加页,但应在明细栏的下方配置标题栏,并在标题栏中填写与装配图相一致的名称和代号。......
2023-06-28

通过此标定曲线即可查出实验室内分析得到的水样浊度值对应的含沙量,由此得到实验现场污染带的浓度分布情况。含沙量各时间段的平面分布图见图4~图6。在沿正南方向距进水口250m以外的范围内、进水口东岸150m以外、进水口西岸530m以外的范围内,湖泊表面含沙量都在20mg/L以下。......
2023-06-26

为了形象地表明沿梁轴线各横截面上剪力和弯矩的变化情况,通常将剪力和弯矩在全梁范围内变化的规律用图形来表示,这种图形称为剪力图和弯矩图。对于非水平梁而言,剪力图可以作在梁轴线的任一侧,并标明正、负号;弯矩图作在梁受拉的一侧。根据剪力方程和弯矩方程判断剪力图和弯矩图的形状,确定控制截面的个数及内力值,作图。在集中力偶作用处,剪力图无变化,弯矩图不连续,发生突变,突变的绝对值等于集中力偶的力偶矩数值。......
2023-06-16

《内经》有“夫十二经脉者,内属于脏腑,外络于肢节。”经脉在体表的分布规律:手三阴从胸走手,手三阳从手走头,足三阳从头走足,足三阴从足走胸腹。十二经脉在头面部的分布规律是:阳明在前(头面部),少阳在侧(头侧部),太阳在后(头后部)。......
2024-01-23

质量数据的集中趋势和离散趋势反映了总体(样本)质量变化的内在规律性。质量数据具有个体数值的波动性和总体(样本)分布的规律性。一般来说,计量连续的数据是属于正态分布。正态分布规律是各种频率分布中用得最广的一种,在水利工程施工质量管理中,量测误差、土质含水量、填土干密度、混凝土坍落度、混凝土强度等质量数据的频数分布一般认为服从正态分布。......
2023-11-19
相关推荐