高层建筑钢筋混凝土结构概念设计成果

2025-09-30 理论教育版权反馈

【摘要】：静力弹塑性分析是在结构上施加一组静力，考虑构件从开裂到屈服、刚度逐步改变的弹塑性计算方法。静力弹塑性分析可以得到结构从弹性状态到倒塌的全过程，因此也称为推覆分析。静力弹塑性分析需要给出的条件为：计算简图、构件参数与荷载，见图3-17。3）得到不同受力阶段下楼层侧移和层间位移角沿高度的分布，结合塑性铰的分布情况可以检查是否存在薄弱层。在静力弹塑性分析中需要计入下降段，往往成为计算程序编制的难点。

静力弹塑性分析（推覆分析Push-over Analysis）是在结构上施加一组静力（竖向荷载全部作用和水平荷载逐步增加），考虑构件从开裂到屈服、刚度逐步改变的弹塑性计算方法。计算时竖向荷载不变（自重及活荷载等），水平荷载由小到大，逐步加载，每一步会有部分构件屈服，屈服的构件需要改变刚度，重新建立刚度矩阵，在增量荷载作用下再进行分析，得到的结果叠加在前一步计算的结果上，如此逐步计算，直到结构达到其极限承载力或极限位移，结构倒塌。静力弹塑性分析可以得到结构从弹性状态到倒塌的全过程，因此也称为推覆分析。

静力弹塑性分析需要给出的条件为：计算简图、构件参数与荷载，见图3-17。图3-17a为计算简图和荷载，与一般静力分析相同，采用平面结构或空间结构，一般都假定楼板在自身平面内为无限刚性；竖向荷载与弹性分析的荷载相同，在分析过程中是不变的；水平荷载则要选择一组尽可能能代表地震作用的荷载分布形式，荷载由小到大，数值改变而分布形式不变。构件计算参数有两部分，除了一般弹性计算时需要的几何尺寸和弹性刚度外，还应给出每个构件力—变形的弹塑性骨架线，一般采用二线性或三线性骨架线（也可采用多折线或曲线），有明确的屈服点和极限承载力（或极限变形）；图3-17b为受弯构件性能，应考虑正向和反向受弯，也可以考虑剪切刚度改变；图3-17c为压弯构件（柱和剪力墙）性能，必须给出轴向力对构件屈服性能的影响，也就是要给出“屈服轨”。

静力弹塑性分析不是新方法，在荷载增量ΔP作用下结构刚度不变，相当于一次“弹性计算”，因此只需将“弹性计算”重复计算n次，每一次的结构刚度都不相同，方法的复杂之处在于每一次计算结束后要重新确定构件的当前状态和刚度，重新建立刚度矩阵。由于该方法能够提供结构的“能力和性能”数据，符合现在正在研究发展的“基于性能设计”的需要，近年来静力弹塑性分析方法得到普遍的重视和广泛研究，在计算的精细程度和解决难点的计算技巧方面得到很大发展。静力弹塑性分析的主要功能有：

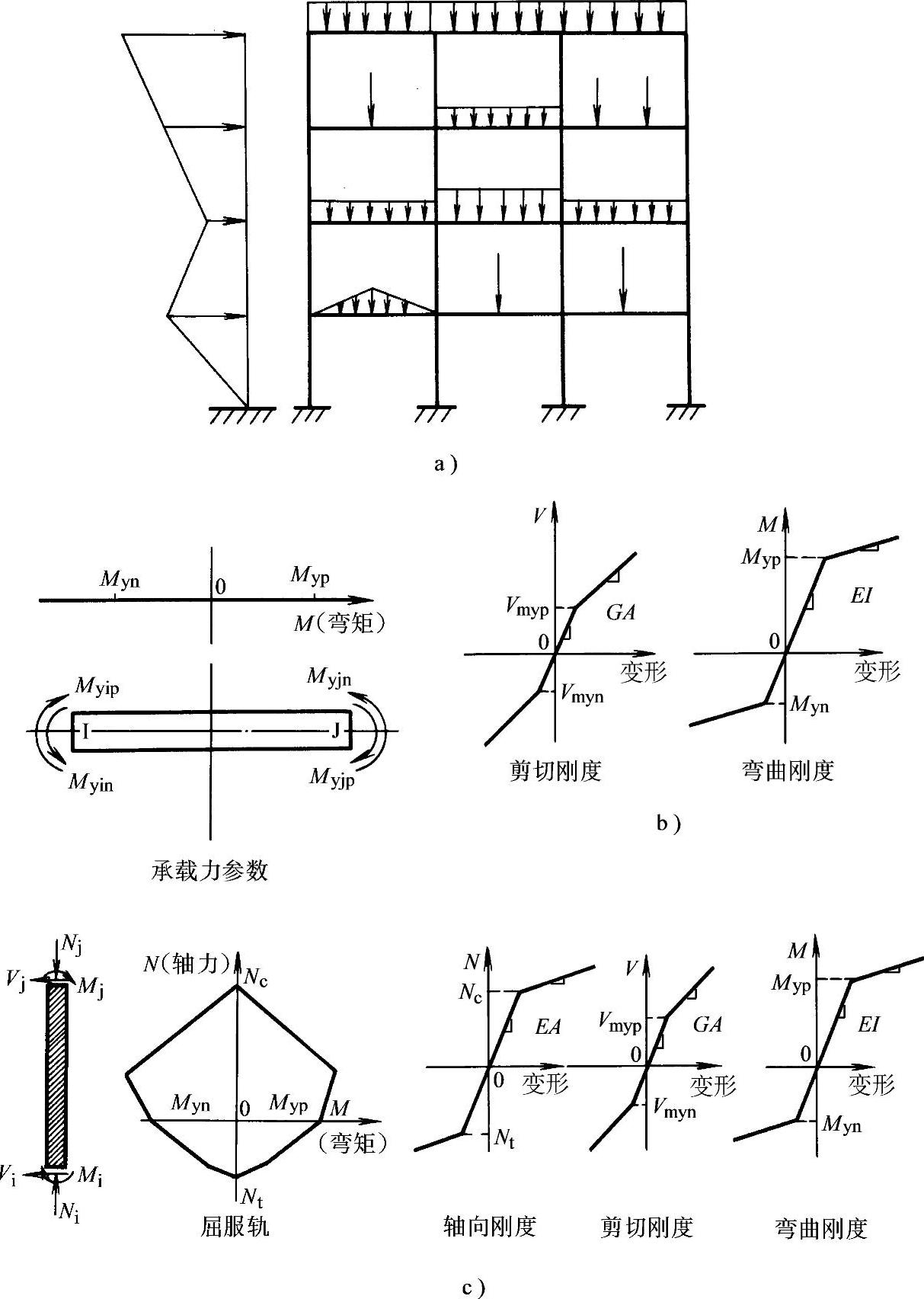
图3-17 静力弹塑性分析

a）计算简图及荷载 b）受弯构件（梁）计算参数 c）压弯构件（柱、墙）计算参数

1）得到结构承受逐步增大的水平荷载作用时内力和变形的全过程，见图3-18a，它综合表示结构在各个阶段的状况，得到结构的最大承载能力和极限变形能力。作出每一层的内力—变形全过程，就可以得到各层层间位移角和顶点位移等重要指标；可以估计相对于设计荷载而言的结构承载力的安全储备大小。

图3-18 弹塑性静力分析结果

a）层剪力—层间变形曲线 b）在某个荷载作用下结构塑性铰分布(https://www.chuimin.cn)

2）得到第一批塑性铰位置和各个阶段的塑性铰出现次序和分布状态，见图3-18b，可以判断结构是否符合强柱弱梁、强剪弱弯等设计要求。

3）得到不同受力阶段下楼层侧移和层间位移角沿高度的分布，结合塑性铰的分布情况可以检查是否存在薄弱层。

4）得到不同受力阶段结构各部分塑性内力重分布情况，结合塑性铰分布，检查多道设防设计意图是否能实现。

5）由结构每一层的层剪力—层间位移角曲线，可以得到弹塑性时程分析需要的各层等效刚度，图3-15中虚线就是静力弹塑性分析得到的一个楼层的层剪力—层间位移角曲线，再拟合成为计算采用的三折线骨架线（实线）。

相对于弹塑性时程分析，静力弹塑性分析要简单一些，其分析的概念、需要的参数和计算结果都更加明确，得到的结构性能比较丰富和详细，构件设计和配筋是否合理都能很直观地判断，容易为工程设计人员了解和接受。但是也存在一些问题：

1）结构计算时施加的水平荷载形式的不确定性。荷载不同，所得结果会有些区别，采用均布荷载所得的极限承载力最大，采用顶点集中力所得的极限承载力最小，倒三角分布荷载的结果居于二者之间。而什么样的荷载能代表地震作用？几乎不可能有明确答案，因为地震作用下惯性力（荷载）分布形式随时间而变化。弹塑性静力分析时，荷载分布形式可以改变一次或两次，但不可能随时改变。目前多数情况取基底剪力法得到的层荷载分布形式、或反应谱分析得到的第一振型地震力分布形式、或振型组合以后的地震力分布形式，基本上类似于倒三角形分布。

2）构件的弹塑性性能需要在材料非线性性能（应力—应变关系）的基础上确定，其中三维构件的弹塑性性能和破坏准则、约束混凝土的性能、塑性铰长度、剪切和轴向变形的非线性性能等都尚需进一步研究和量化。

3）构件在达到最大承载力后荷载开始下降，这时进入“负刚度”阶段，构件的失效一般用最大承载力下降10%～15%来判断。在静力弹塑性分析中需要计入下降段，往往成为计算程序编制的难点。

4）推覆分析只能给出结构在某种荷载作用下的性能，并不能直接得到结构在某一特定地震作用下的表现，推覆分析方法对地震作用下结构状态的判断和评价不如地震反应时程分析的判断更为直接，如果能将推覆分析方法与时程分析方法相结合，即先使用推覆分析，后使用时程分析，或许会更容易对结构进行评价和判断。

高层建筑钢筋混凝土结构概念设计成果

相关推荐