高层建筑钢筋混凝土结构概念设计：弹塑性时程分析的地震反应分析

2023-08-23 理论教育版权反馈

【摘要】：无论是基于承载力延性的抗震设计，还是基于性能的抗震设计，都需要用到弹塑性时程分析或弹塑性静力计算，目前计算软件已有较大改进，应用日益广泛。通常，弹性时程分析采用杆模型，弹塑性时程分析采用层模型；用于研究时采用杆模型，用于设计第二阶段的倒塌验算时，采用层模型等。

无论是基于承载力延性的抗震设计，还是基于性能的抗震设计，都需要用到弹塑性时程分析或弹塑性静力计算，目前计算软件已有较大改进，应用日益广泛。

时程分析法是一种直接的动力计算方法，在结构的基础部位作用一个地面运动（加速度时程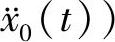，用动力方法直接计算出结构随时间而变化的地震反应。通过计算可以得到输入地震波时段长度内结构地震反应的全过程，包括每一时刻的构件变形和内力，每一时刻的结构位移、速度和加速度，弹塑性时程分析还可以得到杆件屈服的位置、塑性变形等，也可以得到各种反应的最大值，各种反应的最大值并不在同一时刻出现。直接动力分析方法既考虑了地面震动的振幅、频率和持续时间三要素，又考虑了结构的动力特性。时程分析方法是一种较先进的直接动力计算方法。事实上，反应谱就是通过单质点体系的直接动力方法计算得到的。

时程分析方法可用于弹性结构，也可以用于弹塑性结构，应用要点如下^[8][34]：

1.动力计算方法

时程分析方法建立在动力方程的基础上，多自由度体系的动力方程为：

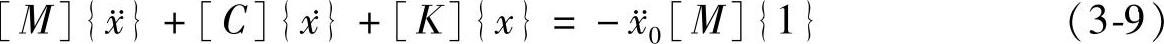
式中 [M]、[C]、[K]——结构的质量矩阵、阻尼矩阵、刚度矩阵；

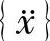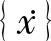、、{x}——结构的加速度、速度、位移反应，都是时间t的函数；

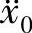——地面加速度，为时间t的函数。

地面运动是随机函数，动力方程不能得到解析解，一般是用逐步积分方法，在已知初始值的情况下在微小时间区段Δt范围内积分求解，得到第i步的结果后，将其作为第i+1步的初始值，再取微小时间区段Δt积分，如此逐步积分得到所有时间区段的数值解。求解动力方程的数学方法很多，常用的有Newmark-β法、Wilson-θ法等。

2.计算模型

结构的计算模型即力学模型，分为杆模型和层模型两大类。杆模型和层模型各有优缺点，可根据计算目的和要求精确程度选择适当的方法。通常，弹性时程分析采用杆模型，弹塑性时程分析采用层模型；用于研究时采用杆模型，用于设计第二阶段的倒塌验算时，采用层模型等。

杆模型以杆件为计算的基本单元，计算简图与弹性分析相同，见图3-10，刚度矩阵的建立方法与构件有限元分析方法相同，自由度的多少和基本假定有关，有平面结构假定和空间结构假定之分，一般都假定楼板在平面内无限刚性，每个楼层的质量集中到楼板高度。杆模型的刚度矩阵是明确的，易于确定，计算可以得到杆件内力和变形随时间变化的全过程，可以找出每个杆件最大内力和最大变形，也可以得到杆件和楼层的位移。计算结果相对精确，但是计算过程长，输出的数据量大。对于弹性时程分析，杆模型应用较多，因为弹性时程分析所用的刚度矩阵与设计计算相同，十分方便，而对于弹塑性时程分析，因为杆件刚度随杆件开裂和屈服而改变，每一步都要重新建立刚度矩阵，费时多，输出的数据量大，而其中设计需要的数据只是少数。

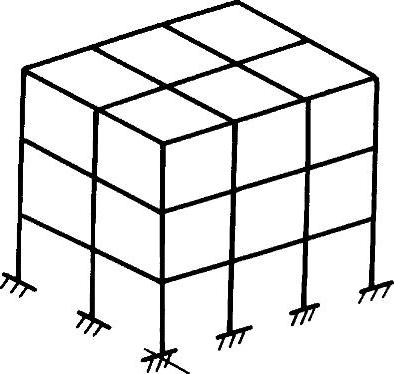
图3-10 杆模型

层模型如图3-11所示，把整个结构视为一根悬臂杆，每个楼层质量集中为一个质点，楼层的刚度凝聚在一根杆中，称为层刚度。根据结构的变形特点和简化假定，层模型又分为剪切型模型、弯曲型模型、弯剪型模型和等效剪切型模型等，它们的刚度矩阵分别包含了剪切刚度GA和弯曲刚度EI，其中等效剪切型模型的刚度矩阵元素排列与剪切型模型类似，等效剪切层刚度的定义为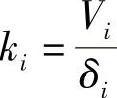，式中V_i、δ_i分别是第i层的层剪力和层位移，是从整体结构的平面或空间分析得到（见弹塑性静力分析），也就是说，每一楼层的层刚度元素k_i都综合考虑了全部杆件的轴向、弯曲和剪切变形。

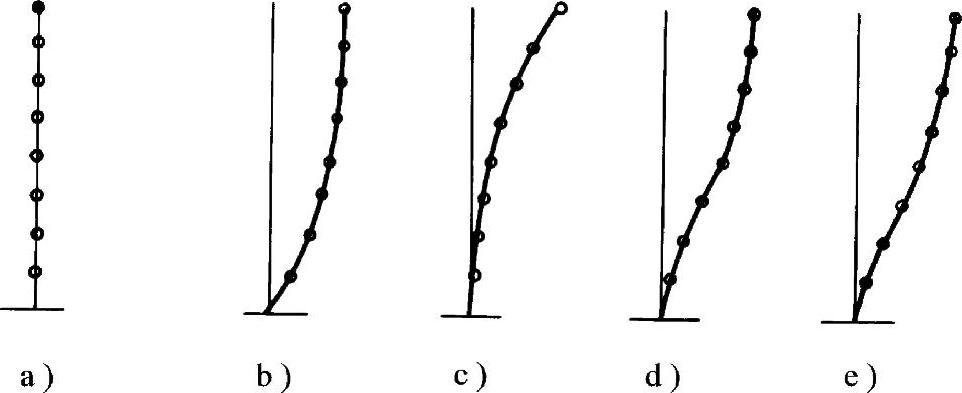
图3-11 层模型

a）集中质量的悬臂杆 b）剪切型模型 c）弯曲型模型 d）剪弯型模型 e）等效剪切型模型

层模型自由度数目少，计算简洁、迅速，计算得到的结果有层剪力、层位移、层间位移角等，可以满足设计第二阶段的层间位移角检验需要，也可以检查结构是否存在薄弱层等。但是层模型计算不能得到杆件的内力和变形，计算结果相对地比较粗糙和笼统，与杆模型相比，是更为近似的分析，一般在设计完成后进行层间变形检验时采用。高层建筑结构首先要用静力弹塑性方法获得杆模型的等效剪切刚度，计算工作量也比较大。

3.恢复力模型

进行弹塑性时程分析时，要给出反复循环地震作用下的杆件刚度，因为开裂、屈服、荷载反向作用等原因，杆件刚度要发生变化。图3-12是在反复循环荷载作用下试验实测的力—位移关系曲线，称为滞回曲线，图3-12a是一般钢筋混凝土弯曲及压弯构件的滞回曲线，图3-12b是剪切变形较大、存在剪切斜裂缝构件的滞回曲线，受力和变形不同的构件滞回性能不同。计算时必须将滞回曲线模型化，给出可用于数值计算的反复循环力—变形的非线性关系，即恢复力模型。恢复力模型既要符合杆件的受力—变形性质，又要便于用数学公式表达，折线形式应用较为方便（也可用曲线表达）。数字化的恢复力模型由两部分组成：骨架线和滞回环。骨架线是滞回曲线的外包线，考虑开裂性能时，可设定为三线性骨架线，不考虑开裂时，可设定为二线性骨架线，见图3-13，骨架线的作用是确定杆件的刚度。滞回环表示杆件在往复荷载下的变形途径（加载、卸载、反向加载……等），刚度退化、强化以及能量吸收、耗散等性能，常用的滞回环模型是在大量试验研究基础上归纳形成的，由于构件性质不同可以得到不同的力—位移关系，也就有不同的模型。图3-14为几种由试验曲线简化的滞回环类型，图3-14a是一般钢筋混凝土压弯构件的性能，图3-14b是剪切变形较大的钢筋混凝土构件性能，图3-14c是钢构件的性能。

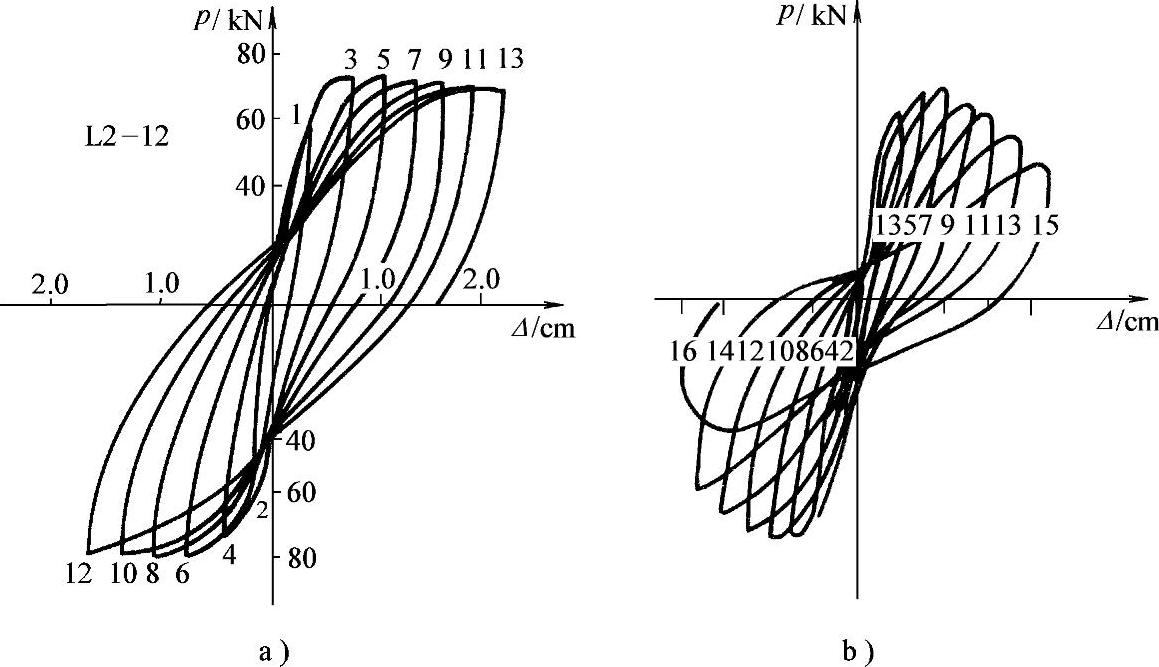
图3-12 试验实测的滞回曲线

a）受弯或压弯构件 b）剪切变形较大、存在斜裂缝的构件

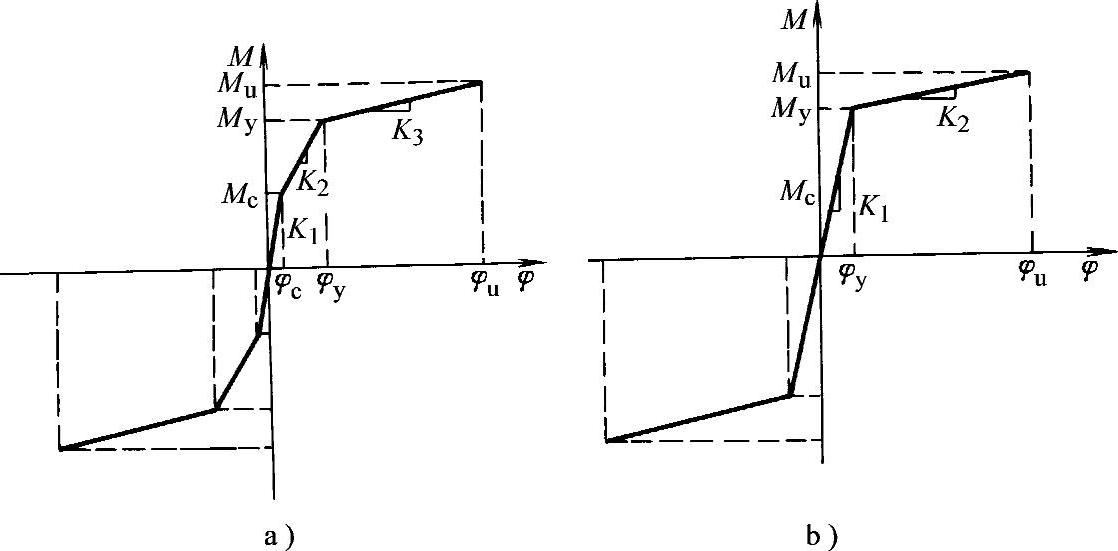
图3-13 骨架线

a）三线性骨架线 b）二线性骨架线

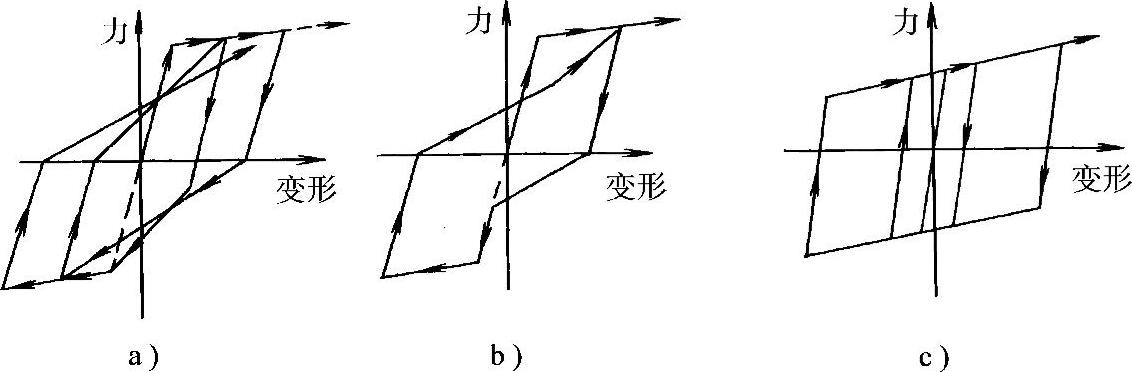
图3-14 滞回环类型

a）钢筋混凝土压弯构件 b）剪切变形较大的钢筋混凝土构件 c）钢构件

在杆模型中，要输入杆件的恢复力模型，杆件的恢复力模型容易确定。

在层模型中，要给出楼层的恢复力模型，包括骨架线和层滞回模型。首先要通过整体结构的静力弹塑性分析得到楼层的V—δ关系曲线，作为层模型骨架线，计算得到的一般是曲线，没有明确的开裂点和屈服点，通常以折线拟合曲线，用三折线或四折线的骨架线可较好地代表结构的层刚度变化，折点虚拟结构的开裂点及屈服点，见图3-15。层模型的滞回环规则根据结构性能假设。

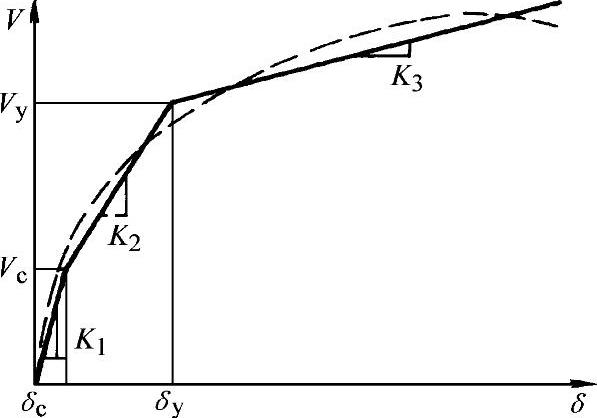
图3-15 层模型的骨架线

4.质量矩阵与阻尼矩阵

为了简化计算，无论在杆模型或层模型中，都假定质量集中在每个楼层，因此质量矩阵都是对角矩阵。

结构阻尼是结构的性能，但是要精确定量却十分困难。在时程分析中做了假定，使阻尼矩阵为刚度和质量的函数，以简化计算。方法很多，其目的都是便于将动力方程中的阻尼项分解，以简化方程求解的过程，常用的阻尼矩阵见式（3-10）。

[C]=α₁[M]+α₂[K] （3-10）

式中，λ_i，λ_j分别为第i、j振型的阻尼比，ω_i，ω_j分别为第i、j振型的频率。

阻尼比λ_i、λ_j应该由实测确定，但是结构高振型的阻尼比尚无一致结论，目前时程分析取值与结构设计统一，取一般公认的阻尼比，钢筋混凝土结构为5%，钢结构为2%，高振型与基本振型相同。

5.输入地震波

地震波是随机振动，影响因素复杂，不同的地震地面运动，结构的反应也不相同，图3-16是1985年墨西哥地震时在墨西哥城SCT站记录的地震波，同时记录了南北水平、东西水平及竖向振动分量（时程分析主要用水平分量）。时程分析证明，同一幢结构用不同的地震波输入，会得到不同的结果，因此如何选择作用在结构所在地的地面地震加速度，成为时程分析的一个难点，也是时程分析结果的一个不确定因素。

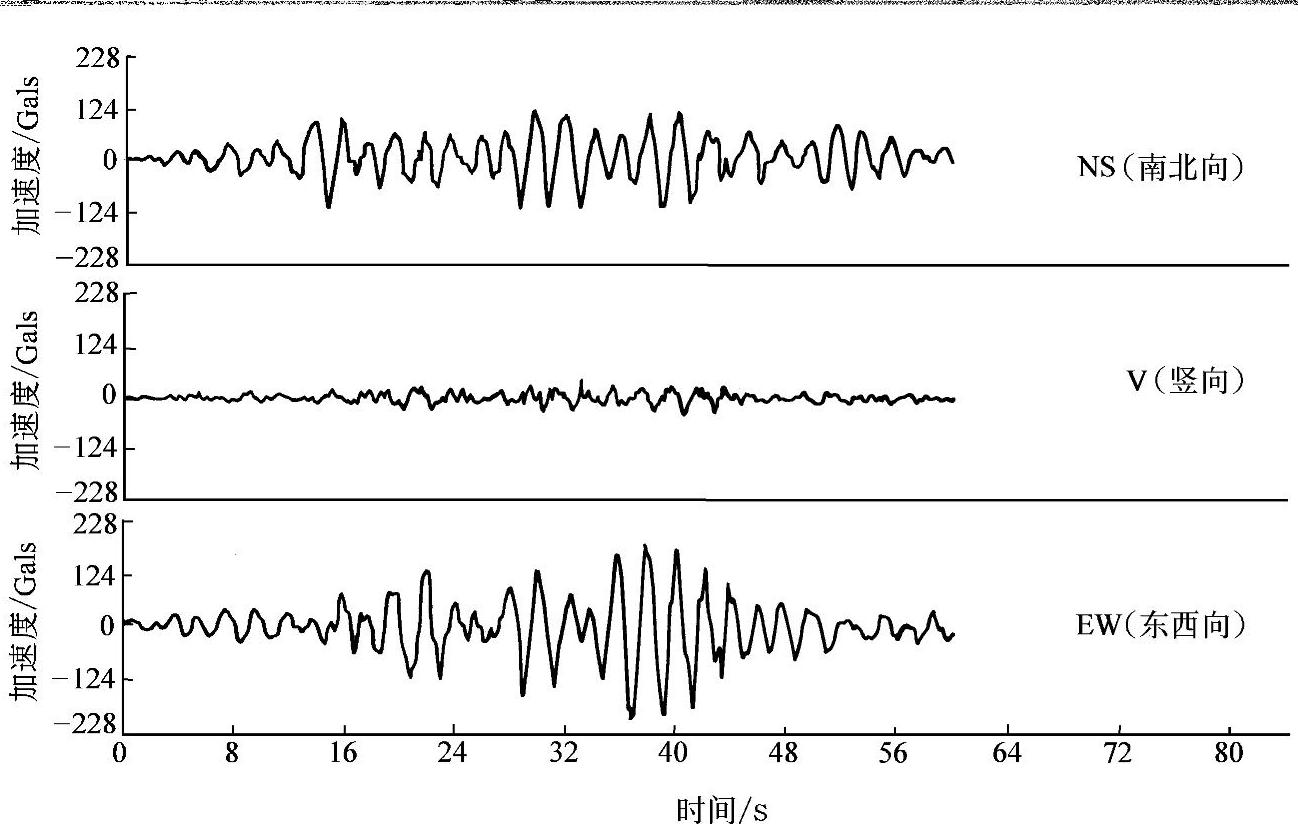
图3-16 1985年墨西哥地震时在墨西哥城SCT站记录的地震波

如果进行建筑物震害分析，可取当地本次地震记录的地震波，比较明确。而设计时，无法预见将来发生的地震，只能选择多条（3条或4条）地震波进行时程分析，以便相互比较和选择合理的计算结果，多条地震波应包括实际地震记录和人工波。最理想的是实际记录的地震波，是本地区历史上曾经记录到的地震波，但是我国历史地震记录很少；近年来我国虽已有了不少记录，但是在大城市的也不多。现在收集到的可供选择的地震记录已较多，设计时所选用的实际地震记录，要考虑其卓越周期和土壤性质，尽可能与当地土壤相近，要使分析结果与反应谱方法有可比性等^[35]。人工地震波是根据当地的场地特性（勘测得到）拟合做成的，但是拟合的人工波有多种可能性（不是唯一的），拟合的人工波不同，计算结果也不会相同。弹性时程分析所用的地震波加速度峰值需调整为当地小震的加速度峰值，弹塑性时程分析所用的地震波加速度峰值则应调整为当地大震相应的加速度峰值。小震和大震的加速度峰值，可由规范查得，也可由当地地震危险性分析得到。

时程分析法比反应谱方法前进了一大步，主要的优点是可以得到结构的地震反应全过程，便于判断结构在地震作用下的表现是否符合设计要求。特别对于结构研究和地震震害的分析，该方法比较有效，已经在国内外普遍应用，并获得很多成果，在第4章、5章、7章中有一些关于国内外震害分析和研究应用的实例介绍。第10章的一些工程实例介绍中也有关于设计工作中弹性和弹塑性分析的应用情况。

从以上的介绍可见，弹塑性时程分析方法是先进的，但是在应用上还有很多困难和局限，尤其是输入地震波的不确定性，结构性能的近似假定和模拟等，使结果的可信度受到限制；该方法需要专门的程序和运用知识，输入、输出数据量大，计算技术复杂，一般需要专门的技术人员和结构设计人员共同进行分析，不能盲目地使用计算结果。规范只要求少数重要、高度大而柔或有薄弱部位的结构，用弹塑性时程分析进行大震作用下的变形校核或性能设计。我国新抗震规范中已给出了弹塑性时程分析的要求，例如地震波选用要求、罕遇地震作用的峰值加速度、允许层间位移角等。

高层建筑钢筋混凝土结构概念设计：弹塑性时程分析的地震反应分析

相关推荐