首先进行尝试性分析。根据原有变量的相关系数矩阵，采用主成分分析法提取因子，并列出其特征根值。如下图所示为因子碎石图，其横坐标为因子数目，纵坐标为特征根，根据特征根大于或等于1的判断准则，以及考虑累计贡献率为70%～85%的准则，碎石图显示第四个因子开始特征根很小，对解释原有变量的贡献很小，成为可以被忽略的“高山下的碎石”，因此在计算中取三个因子。
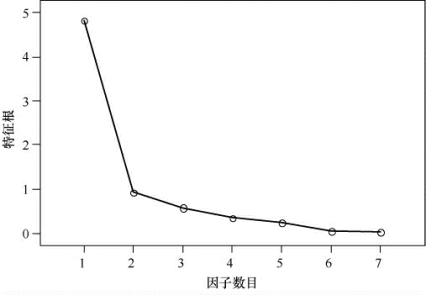
因子碎石图
取三个因子时，因子解释原有变量总方差的情况见表7－3，抽取方法采用了主成分分析法。由表7－3可以看出，当取三个因子时，可以解释原有变量总方差的90．488%（＞85%），总体上原有变量的信息丢失很少，因子分析效果较合适。
表7－3 因子解释变量总方差的情况
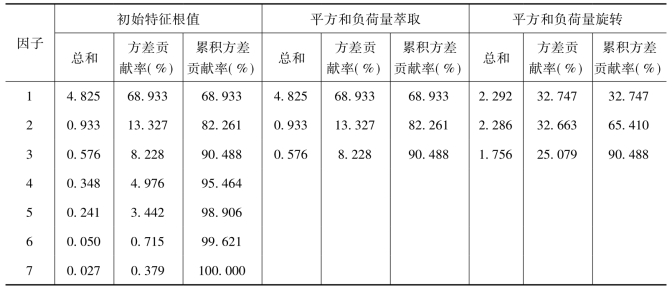
取三个因子时，经过方差最大法正交旋转后得到的因子载荷矩阵见表7－4，协方差矩阵见表7－5，抽取方法采用了主成分分析法，旋转方法采用Kaiser方差最大旋转法，经过五次旋转迭代。对该旋转后的载荷矩阵，根据各共同因素中情感词项的因子负荷量的大小进行了排序，便于考查各个因子所解释的词义变量。
表7－4 因子载荷矩阵
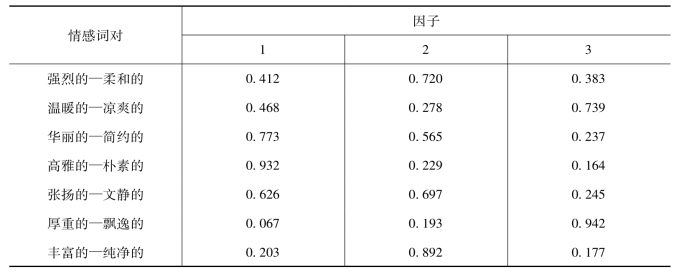
表7－5 因子协方差矩阵
因子分析中，每个因子所关联的词义之间都具有很大的相关性，而每个因子之间却是相互独立的。
“强烈的—柔和的”、“温暖的—凉爽的”、“华丽的—简约的”、“高雅的—朴素的”、“张扬的—文静的”、“厚重的—飘逸的”、“丰富的—纯净的”七对情感词的面料情感描述值不妨分别用E1，E2，…，E7来表示。根据因子载荷矩阵，可以把每对情感变量表示为三因子的线性组合，得出因子分析模型为：
其中f1、f2、f3为因子。同时，采用回归法估计出因子得分系数，得到的因子得分系数矩阵见表7－6。抽取方法也采用了主成分分析法，旋转方法采用Kaiser方差最大旋转法。
表7－6 因子得分系数矩阵
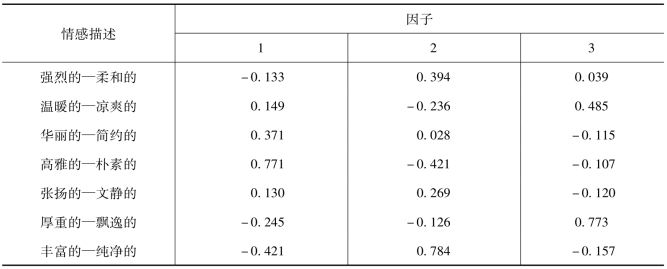
根据表7－6得出的因子得分函数为：
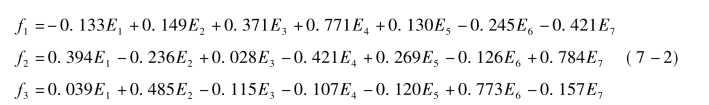
根据因子得分系数矩阵，可以由每个图像样本的七对情感评估值，计算得出三个因子的值。作为共同因子，各因子分别对应着不同的情感语义。由因子得分系数矩阵看出，第一个因子能较好的解释“高雅的—朴素的”、“丰富的—纯净的”、“华丽的—简约的”这三组词义；“丰富的—纯净的”、“高雅的—朴素的”与第二个因子相关程度高，第二个因子主要解释了这两个语义；第三个因子则主要对应着情感词对“厚重的—飘逸的”和“温暖的—凉爽的”。这三个因子之间是相互独立的，且对初始七对情感语义形容词的解释程度高达90．488%，表明可以使用这三个因子来概括描述服装面料图像的七对情感语义，且信息损失较小。
有关基于内容的服装图像情感语义识别和检索的文章
柴油机的热流测量方法与汽油机类似。柴油机也同样表现为每个循环的热流曲线之间有很大的变化。试验条件是压缩比为16，转速为2000r/min，当量比为φ=0.5，进气系统压力为1.5×105Pa。图8-20 中间涡流柴油机热流涡流较小的柴油机活塞凹部的平均热流通常比活塞冠部环状壁部位和气缸盖部位的平均热流高。图8-21 自然进气柴油机的气缸盖与气缸套处热流Praum计算求出活塞壁面与气缸盖面的热传递率h1，以及气缸套面的热传递率h2，并比较判定后者为前者的1/3，即h2=1/3h1......
2023-06-28
，σ（αn）是线性无关的.因此，n≤m.综合上面的结论可以得到n=m，即V1，V2有相同的维数.充分性.设V1，V2都是n维线性空间，下面我们来建立一个从V1到V2的同构映射，从而证明V1V2.分别取V1的一组基α1，α2，…，αn之下的坐标是唯一确定的，而向量组β1，β2，…......
2023-11-22
本书模型中，城市内、外部的具体组分对城市最优规模的影响没有做明确鉴别，所以模型并不能完全解释城市的实际运行规律。城市最优规模是一个不断发展的、动态的变化过程，因此需要用动态的观点进行研究，可利用普利戈金的耗散结构理论进行更进一步的深入探讨。目前我国正处于城市化发展的转型时期，城市最优规模的研究对城市发展实践将有科学的指导意义。......
2023-11-22
但初期的问卷调研结果却出乎意料。为此，如何通过进一步的调研摸清教师真实的反思水平，是研究需要解决的下一个问题。因此，也有了下文笔者不厌其烦地从多个角度对教师反思水平现状的调研。通过更为深刻的情境题目、水平测试卷等内容的分析，教师的一般的反思水平状况呈现出来。......
2023-08-05
PISA采用按照概率与抽样元素的规模大小成比例的抽样法，是以上海所有的在7年级及以上就读的15岁学生作为调查总体，首先采用与学生规模等概率抽样的方法抽取学校样本，然后在每所样本学校随机抽取同样数量的学生。第二阶段是学生抽样，由SHPISA研究中心根据PISA协作组织反馈的样本学校名单，收集这些学校所有15岁学生的名单，与前期各学校提交的学生数据核对。中国上海共计抽取了符合PISA参加资格的学生6 467名。......
2023-10-19
调整第Ⅲ区段周边原有的车行道及人行道至整治区域外，具体道路选址需符合齐长城总体保护规划要求。齐长城临朐桲根腿东岭段第Ⅲ区段断面示意图（四）第Ⅳ区段以现状保护为主，结合考古勘探设立齐长城遗址保护区域，并在该区域内进行绿化环境整治。......
2023-11-02
根据海洋生态学，海洋生态系统是占据一定空间的自然界客观存在的实体，是生命系统和环境系统在海洋这个特定空间的结合体。海洋生态系统内的生物和非生物组分通过物质循环和能量流动而相互作用，因此，海洋生态系统的各组分是相互依存的，表现出丰富的生物多样性的特点。......
2023-11-09
晚上大约7：20左右，村民选举委员会主任宣布：鲁顺才，得主任票1314票，当选古城村第二届村委会主任；刘映芳，得副主任票1235票，当选为古城村第二届村委会副主任；委员候选人杨发明得1427票、方树英得1414票、田俊坤得1267票、段家林得1259票、沐玉鸿得1115票，他们当选为古城村第二届村委会委员。......
2023-11-27
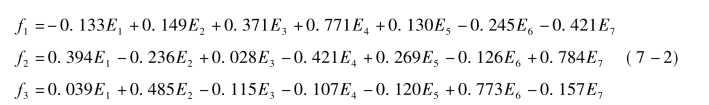
相关推荐