图像的冷暖描述参见式（2－4）的冷暖色隶属函数。上述分析与本节开始的分析大体一致，显示出男西装图像在色彩饱和度和冷暖特征上的区别，饱和度与冷暖隶属函数能够较好地描述图像的饱和度和冷暖分布，有利于实现第二个情感因子的推导。......
2025-09-30
BP神经网络的理论在图像情感识别中的应用
【摘要】：BP神经网络即反向传播网络，它是前向网络的核心部分，也是人工神经网络的精华部分。BP神经网络是目前应用最广的神经网络之一，BP神经网络是由一个输入层、一个或多个隐层以及一个输出层组成，上下层之间实现全连接，而每层神经元之间无连接。
BP神经网络即反向传播网络，它是前向网络的核心部分，也是人工神经网络的精华部分。因具有结构简单、可塑性强等优点，故BP神经网络及其改进形式被广泛应用在函数逼近、模式识别、信息分类及数据压缩等领域。
BP神经网络是目前应用最广的神经网络之一，BP神经网络是由一个输入层、一个或多个隐层以及一个输出层组成，上下层之间实现全连接，而每层神经元之间无连接。网络的学习过程包括正向传播和反向传播。在正向传播进程中，输入信息从输入层经隐层加权处理传向输出层，经功能函数运算后得到的输出值与期望值进行比较，若有误差，则误差反向传播，沿原先的连接通道返回，通过逐层修改各层的权重系数，减小误差。随着这种误差逆向传播修正的不断进行，网络对输入模式响应的正确率也在不断上升。
多层BP网络具有输入节点、一层或多层隐节点和输出节点，结构如图4－2所示。这种网络使用非线性可微分函数进行权值训练，通常采用Sigmoid函数（正切函数tansig或对数函数logsig）和线性函数purelin作为传递函数（又称激活函数）。
设tpi，Opi分别是网络的期望输出和计算输出，则网络第p个样本的误差为：
BP网络的学习实质上就是求取误差函数最小值的问题，这种算法采用学习规则，按误差函数的负梯度方向修改权值。
图4－2中，xj表示输入层第j个节点的输入，j=1，…，M；wij表示隐含层第i个节点到输入层第j个节点之间的权值；θi表示隐含层第i个节点的阈值；φ（x）表示隐含层的激励函数；wki表示输出层第k个节点到隐含层第i个节点之间的权值，i=1，…，q；ak表示输出层第k个节点的阈值，k=1，…，L；ψ（x）表示输出层的激励函数；Ok表示输出层第k个节点的输出。
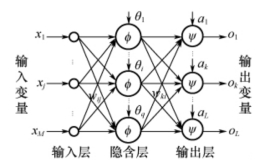
图4－2 三层BP神经网络
（1）信号的前向传播过程：
隐含层第i个节点的输入neti：
隐含层第i个节点的输出yi：
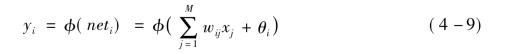
输出层第k个节点的输入netk：
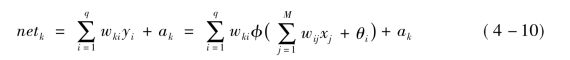
输出层第k个节点的输出ok：
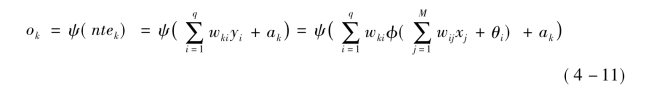
（2）误差的反向传播过程：
误差的反向传播，即首先由输出层开始逐层计算各层神经元的输出误差，然后根据误差梯度下降法来调节各层的权值和阈值，使修改后的网络的最终输出能接近期望值。
对于每一个样本p的二次型误差准则函数为Ep：
系统对P个训练样本的总误差准则函数为：(https://www.chuimin.cn)
根据误差梯度下降法依次修正输出层权值的修正量Δwki，输出层阈值的修正量Δak，隐含层权值的修正量Δwij，隐含层阈值的修正量Δθi。
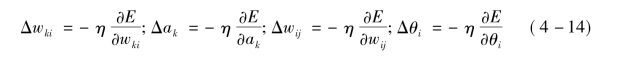
式（4－14）中，负号表示梯度下降，常数η为比例系数。输出层权值调整公式：
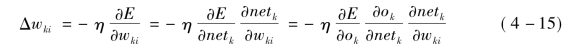
输出层阈值调整公式：
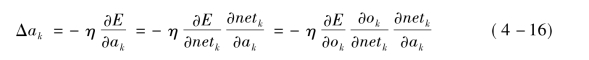
隐含层权值调整公式：
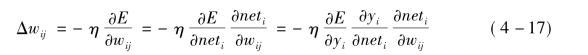
隐含层阈值调整公式：
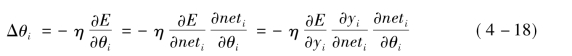
又因为：
所以最后得到以下公式：
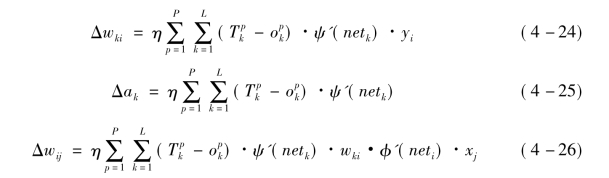
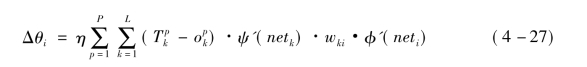
BP神经网络的训练过程为：
（1）用小的随机数对每一层的权值和偏差初始化，以及设定期望误差值、学习速率、最大循环次数。
（2）计算网络各层输出矢量，以及网络误差。
（3）根据学习规则计算各层反传的误差，并计算各层权值和偏差的修正值以及新权值和偏差。
（4）再次计算权值和偏差修正后误差。
（5）检查误差是否小于误差值，如果是或超过最大循环次数训练结束，否则继续。
相关文章
- 详细阅读
-
彩色对比度描述在服装图像情感语义识别和检索中详细阅读
由于第二个情感因子还与图像的彩色对比度有密切联系，故本文仍采用式（2－7）所定义的一幅图像的彩色对比度。本章基于男西装图像的颜色对其情感语义特征进行了分析，初步结果为亮度—冷暖直方图能够较好地描述男西装图像的因子1所解释的情感，其归一化的模糊直方图十维特征可作为估算因子1的图像特征。研究结果为下一步探讨如何利用这些图像低层特征进行男西装图像情感语义的识别和检索打下基础。......
2025-09-30
-
基于内容的服装图像情感识别和检索详细阅读
长期以来，由于人类情感的主观性和服装情感描述的模糊性，截至目前对服装情感的认识大多仍停留在定性阶段。而随着人工智能技术的发展及人们对服装品位的日益苛求和着装情绪化，我们认为是时候把对服装情感的研究和应用提升到“定量”阶段了。基于此，我们提出了“服装情感学”的概念，并把人工智能有关理论引入服装领域，结合心理学、感性工学等学科的研究成果，对服装情感进行量化研究，以期达到对服装情感的定量描述和量化评价。......
2025-09-30
-
基于内容的服装图像情感识别与检索结果详细阅读
在图3－4所示状态下点击“图像特征提取”按钮，显示其首页页面，如图3－10所示。图3－13因子1输出文本截图图3－14因子2输出文本截图至此，经过以上步骤，男西装图像的低层特征数据就可以通过程序自动算出，为BP神经网络训练和学习做好了准备。......
2025-09-30
-
基于内容的服装图像情感语义识别和检索详细阅读
目前，将神经网络应用于图像识别的文献很多［1，2］，但用于服装图像的情感语义识别和检索还几乎没有，而本章及第4、第5章正是采用了神经网络对男西装图像情感语义识别和检索问题进行了探讨。图3－1男西装图像样本神经网络训练和入库的流程图3－3男西装图像情感语义检索的流程BP神经网络是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。......
2025-09-30
-
水平集方法在图像处理中的应用详细阅读
由于XFEM 允许不连续面穿过单元，即网格独立于间断面，因此需要对不连续面进行几何描述，常用方法为水平集方法 。水平集方法是一种用来追踪间断运动的数值方法。图6－1水平集函数f 和g 表示的二维裂纹在水平集方法中，与空间、时间有关的零水平集函数f用来描述与网格无关的间断。......
2025-09-29
-
纹理特征及其在图像处理中的应用详细阅读
纹理是人类视觉系统对自然界物体表面现象的一种感知，是人们描述和区分不同物体的重要特征之一。同时，纹理是一个区域特征，与观察尺度相关。所以，纹理特征可以认为是图像中灰度、颜色或细小的结构形状在空间上呈现规律的变化［70］。纹理基元具有面积、周长、偏心率、方向、延伸度、矩等特征。......
2025-09-29
-
射频识别技术在智能制造中的应用探析详细阅读
将RFID技术与制造技术相结合，可有效提升制造效率、制造品质和企业管理水平。RFID技术在智能制造中的应用主要有以下几个方面：1.RFID技术的数字化车间RFID在数字化车间中的应用主要包括产品管理、设备智能维护、车间混流制造。目前，RFID技术已经在车间物流管理、SCM及物流园管理中得到成功应用，可进一步推广应用到制造企业全物流管理系统中。......
2025-09-29
相关推荐